889 results

PERIODICAL PIECEWISE CUBIC HERMITE INTERPOLATING POLYNOMIAL: THE FUNCTIONS PERPCHIP AND PERSPLINE

The functions pchip and spline of matlab are adapted to the periodical case: perpchip and perspline. Some examples are given

Separating periodic signals from their aperiodic background

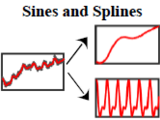
"Sines and Splines - Variable Projection" demonstrates the separation of a signal into its periodic and aperiodic portions, whereby the period of the periodic portion is unknown. Therfore the signal

Computes the B-spline approximation from a set of coordinates. Supports periodicity and n-th order approximation.

Computes the B-spline approximation from a set of coordinates (knots).The number of points per interval (default: 10) and the order of the B-spline (default: 3) can be changed. Periodic boundaries

Implements a model for Cubic Smoothing Splines with periodic boundary conditions

Smoothing cubic splines are implemented with periodic conditions, so that closed curves in any dimension can be approximated. It includes a test function to demonstrate it.Theoretical arguments

Least squares approximation of 1D data using free-knots spline

The purpose of this function is to provide a flexible and robust fit to one-dimensional data using free-knot splines. The knots are free and able to cope with rapid change in the underlying model

Least squares spline modeling using shape primitives

If you could only download one curve fitting tool to your laptop on a desert island, this should be it.For many years I have recommended that people use least squares splines for their curve fits

Fit a spline to noisy data

controlled by the selection of breaks. SPLINEFIT:- A curve fitting tool based on B-splines- Splines on ppform (piecewise polynomial)- Any spline order (cubic splines by default)- Periodic boundary conditions

Find connected components of periodic binary data.

bwconncomp() determines connected components of a binary image, but the image may actually represent data on a periodic domain. In this case, CC2periodic() appropriately converts the output of

Draw, manipulate and reconstruct B-splines.

The package comprises of a graphical utility to place uniform B-spline control points and see how the B-spline is redrawn as control points or control point weights are adjusted, and functions to

A non-local learning rule is employed in a repetitive neurocontroller based on B-spline network.

http://dx.doi.org/10.1109/IECON.2013.6700120 [**] weight constraints are used instead of forgetting and that turns out to robustify the controller. Hence, the same idea has been tested also in the B-spline based repetitive neurocontroller

Application for Fourier series analysis of periodic signals

B-spline registration of two 2D / 3D images or corrsp. points, affine and with smooth b-spline grid.

Affine and B-spline grid based registration and data-fitting of two 2D color/grayscale images or 3D volumes or point-data. Registration can be done intensity / pixel based, or landmark /

Distance based interpolation along a general curve in space

is to be a spline, perhaps interpolated as a function of chordal arclength between the points, this gets a bit more difficult. A nice trick is to formulate the problem in terms of differential

Compute spline function and its derivative

Some set of tools that allows to interpolate on grid a spline function and compute its derivative.Multi-dimensional supported (but rather slow)Natural / Not-a-knot / periodic conditionsIt is still a

Evaluates and plot 2D Cardinal Spline (Catmull-Rom) Spline.

EvaluateCardinal2D.m--------------------Evaluates 2D Cardinal Spline at parameter value u.EvaluateCardinal2DAtNplusOneValues.m------------------------------------Evaluate cardinal spline for given

Matlab funcions for performing landmark warping using thin plate splines

thin plate spline warping, inverse distance weighted interpolation

Demonstrates the use of thin plate splines based warping for temporal interpolation.

Spline object modification / transformation

A little piece of code enabling quick modification of spline objects: clipping, shifting, and scaling in both x, and y.

N -Dimensional cubic Cardinal spline (Catmull-Rom) Interpolation

Cardinal(Catmull-Rom) Spline Interpolation for given four control points using uniform parameterization. Each control point can be N-Dimensional Euclidean space.----------------------------------A

Dialog for selecting elements from periodic table

The function creates a periodic table for user input. It can be used stand-alone or in a complementary fashion with the Mole Package by Gerhard Nieuwenhuiys.Features include highlighting certain

Spline toolbox for the definition, evaluation and visualization of spline curves and surfaces based on standard B-splines

The Spline toolbox allows the definition, evaluation and visualization of spline curves and surfaces based on standard B-splines. Furthermore, it provides an approximation algorithm with the

This GUI visualizes the basis functions of spline spaces

This GUI visualizes the basis functions of spline spaces. Different bases can be chosen from the following: 1) B-Splines 2) Cardinal Splines

1D and 2D splines

`Splines` is a set of C++ classes (with MATLAB mex interface) which implements varios spline interpolation.The classes are the following: - ConstantSpline, for piecewise constants functions -

two-point spline with slope constraints

This function computes a two-point spline with end-point slope constraints as a section of a Cornu spiral. (The screenshot was generated with the demo code at the end of cornu_spline.m.) The

Create, manipulate, differentiate, and integrate splines

Extensive and flexible creation and manipulation of 1-D piecewise polynomials. Handles different spline end constraints. Finds derivatives and integrals, inverse interpolates, breaks apart, evaluates

Fits the so called restricted cubic spline via least squares and obtains 95% bootstrap based CIs.

%Fits the so called restricted cubic spline via least squares (see Harrell %(2001)). The obtained spline is linear beyond the first and the last %knot. The truncated power basis representation is

Fit, evaluate, differentiate non-uniform B-splines of any order - fast

fastBSpline - A fast, lightweight class that implements non-uniform B splines of any order Matlab's spline functions are very general. This generality comes at the price of speed. For large-scale

This project introduces a fast maximum power point tracking (MPPT) method for PV systems. The method is based on spline interpolation.

The attached file contains simulations of the following paper:Novel Spline-MPPT Technique for Photovoltaic Systems Under Uniform Irradiance and Partial Shading

International Reference Ionosphere 2012 model

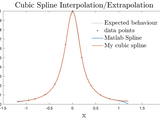
A vectorized, parallel capable, cubic spline interpolation/extrapolation function for non-uniformly distributed 1d data

The publication of this function was inspired by the poor job done by several implementations of the 1d cubic spline publications in Matlab's file exchange repos.This function was part of one of my

determina los polinomios del spline natural de frontera liobre

Al introducir los valores de x y y a interpolar le halla los parametros y muestra las ecuaciones de forma grafica y numerica,spline cúbico natural o con frontera libreIngrese Los valores de x [x0

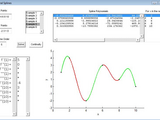
A GUI that plots and gives equations for variable order intermediate splines.

GSP is a graphical user interface which takes x and y points as inputs, along with the order m, then outputs mth order splines between each of the x points. In most cases additional constraints are

Obtains a piecewise cubic spline from a function, and a function to obtain derivatives is included.

Design of a Log-Periodic Dipole Antenna

This MATLAB code gives the complete design of a Log-Periodic Dipole Antenna (LPDA) provided the directivity and required bandwidth are known.

The active geometric shape model is a novel approach for fitting geometric shapes in images.

This function fits a polynomial splines of order m to a given data (x,y). it is valid for one dimension only.

% This function fits a polynomial splines of order m to a given data (x,y).% it is valid for one dimension only.% the function uses interpolation approach so it is not suitable for% noisy

Thin plate splines can be used to interpolate nonuniform data, such as the Radiohead dataset, which

A thin plate spline radial basis function network may be used to interpolate non-uniformly spaced data. The surface (or line or hypersurface) is fit exactly to the given control points, with the

Basic toolbox for polynomial B-splines on a uniform grid. OO overloading of common operators.

B-splines is a natural signal representation for continous signals, wheremany continous-domain operations can be carried out exactly once theB-spline approximation has been done.The B-spline

Implements Immiscible Lattice Boltzmann (ILB, D2Q9) method for two phase flows

This function fits a polynomial splines of order m with pth continuous derivatives to a given data (x,y).

% polysplinefitc% This function fits a polynomial splines of order m with pth continuous% derivatives to a given data (x,y).% it is valid for one dimension only.% the function uses

This is an interactive GUI illustrating Periodic Spirals. Read the description before download.

Analysis of Periodic, Aperiodic & Odd, Even Signal Via GUI

Analysis of Periodic, Aperiodic & Odd, Even Signal Via GUI

To calculate the trajectory of a ballistic baseball with air drag, wind pressure, and magnus force (lift or curve).

Determine the locations of local maxima and minima in a pp spline generated by pp = spline(x,Y);

This function uses vectorised methods to determine the locations of maxima and minima where they exist within a piecewise spline fit. The matlab built-in functions for determining the maxima and

A fast circular cross correlation algorithm for periodic signals, using the FFT.

Uses fft to calculate the circular cross correlation of two periodic signal vectors.This is equivalent to xc(k)=sum(u1.*circshift(u2,k)), but much faster (on the order of 500 times faster for a 1024

MATLAB interface to aid in plotting of VMEC output.

Matlab Implementation of the paper "Adaptive Gaussian Notch Filter for Removing Periodic Noise from Digital Images"

Matlab Implementation of the paper Varghese, Justin, et al. "Adaptive Gaussian Notch Filter for Removing Periodic Noise from Digital Images" IET Image Processing, Institution of Engineering and

atmospheric conditions to 2000km

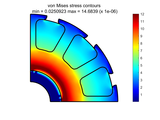
Finite element library for solving plane elasticity problems

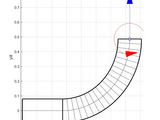
Planar Cosserat rod

Function to smooth call option prices and implied volatilities free of static arbitrage.

smoothing splines under shape constraints to estimate call option prices as a function of strike and time-to-maturity. Based on these prices, implied volatilities can be obtained.

3D TPS warping function

Image analysis for Jet-in-crossflow data.

image data.Automated analysis for Sauter mean diameter of droplets, periodic features of the jet, and droplet and void statistics are possible with Xflow.Background reduction using user-selected

Numerical computation with functions

A toolbox for Matlab, for solving continuous time trajectory optimization problems

A Simulink library for wavelet processing on 1-D signals

GIBBON: The Geometry and Image-Based Bioengineering add-ON for MATLAB

MATLAB functions for processing data from the Vienna Ab initio Simulation Package (VASP).

hyperdistance from NEB calculation.neb_spline(directory,N)Fit energies and forces of a NEB calculation using a spline.num_images()Determine number of images used in a NEB calculation.number2chemsym(Z)Get the

This is a suite of simple utilities that allow for efficient approximation of complex functions in a

This tool accepts a function handle for a "well behaved" function. It then automatically finds the best position for the knots for cubic spline approximation based on the error tolerance specified by

Gaussian Process Regression using GPML toolbox V4.2