Find the best fit for an ellipse using a given set of points (a closed contour).

This function uses the Least-Squares criterion for estimation of the best fit to an ellipse from a given set of points (x,y). The LS estimation is done for the conic representation of an ellipse

A tool set for fitting and/or plotting various conics and quadric surfaces, e.g., ellipses, cylinders, spheres, planes, cones, and lines.

This FEX submission offers a tool set for fitting and plotting 2D conics (ellipses, circles, lines,...) as well as 3D quadric surfaces (ellipsoids, spheres, planes, cylinders, cones,...). Each type

Fits an ellipse to a set of points on a plane; returns the coefficients of the ellipse's equation

This is a fast and non-iterative ellipse fit. Usage: A = EllipseDirectFit(XY)Input: XY(n,2) is the array of coordinates of n points x(i)=XY(i,1), y(i)=XY(i,2) Output: A = [a b c d e f

Fits an ellipse to a set of points on a plane; returns coefficients of the ellipse's equation.

This is a fast non-iterative ellipse fit, and among fast non-iterative ellipse fits this is the most accurate and robust. It takes the xy-coordinates of data points, and returns the coefficients of

Representation of a given 2D shape with an automatically determined number of ellipses.

ellipses, so that the total area covered by the ellipses is equal to thearea of the original shape without any assumption or prior knowledge about theobject structure. To solve this interesting theoretical

Elliptical scanning algorithm for image labeling in corneal topography

This algorithm detects the labels of the rings in a placido ring image which can be extremely helpful for corneal topography.Note: Tilt of the ellipse has not been used for updating ellipse

GIBBON: The Geometry and Image-Based Bioengineering add-ON for MATLAB

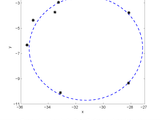
Given a set of points (x, y) this function returns the best fit ellipse.

Usage:[semimajor_axis, semiminor_axis, x0, y0, phi] = ellipse_fit(x, y)Input: x - a vector of x measurements y - a vector of y

Estimates the ellipse parameters and their uncertainties

EllipseFit4HC is an ellipse fitting algorithm based on first order Taylor expansion (linearization) of the originally nonlinear model. EllipseFit4HC is suggested for uncertainty evaluation of the

MVTec Halcon function mex-wrapper

Fit ellipses to 2D points using linear or nonlinear least squares

There are two main methods for least squares ellipse fitting:1) Minimise algebraic distance, i.e. minimise sum(F(x)^2) subject to some constraint, where F(x) = x'Ax + b'x + cThis is a linear least

Ellipse fits using geometric parameters based on Levenberg-Marquardt minimization scheme.

matrix.Usage: [ParG,RSS,iters] = fit_ellipseLMG(XY,ParGini,LambdaIni)Child functions:Residuals_ellipse(from previous submission) , JmatrixLMG (included in the main function)Input:XY:given points i=1 to nParGini

I have cleaned up the scripts and uploaded two examples

This is my collection of scripts for fitting contact angles of tilted drops. There is two methods, polynomial fitting and double sided elliptical fit. A description of the latter method have been

Fit ellipses, ellipsoids and other quadratic curves and surfaces to noisy data.

ellipse fit by Fitzgibbon et al. [1] and direct ellipsoid fit by Qingde Li and John G. Griffiths [4], the toolbox features an estimation algorithm by the author [2,3], based on and extending the work of

Sandia Matlab AnalysiS Hierarchy

Region-based Fitting of Overlapping Ellipses and its Application to Cells Segmentation

This code is a simple implementation of METHOD RFOVE PROPOSED IN [1], a Region-based Fitting of Overlapping Ellipses and its Application to Cells Segmentation. RFOVE is completely unsupervised

The quantitative results are computed based on the synthetic nuclei BBBC005 datasets.

processes image data containing connected ellipses. we try to fit a gaussian mixture to ellipses.

the pixels in an image are weighted with their intensity. we try to fit a pre-defined number of connected (partially overlapping) ellipses onto this image, using gmdistribution.fit from matlab

Ellipse fit using geometric parameters based on Trust Region minimization scheme.

This is a version of ellipse fit when applying Trust Region minimization scheme.The most accurate and robust fit minimizes geometric (orthogonal) distances from the observed points to the fitting

Automatic creation of anatomical coordinate system on the knee bones (Femur, Patella and Tibia)

Corneal Topography: Constructing Curvature Topography from Placido Rings Image

JAABA: The Janelia Automatic Animal Behavior Annotator

An efficient ellipse detector based on Hough voting

Overview: Fits an ellipse by examining all possible major axes (all pairs of points) and getting the minor axis using Hough transform. The algorithm complexity depends on the number of valid

plot_ellipse simply plots an ellipse arround scattered points with 95% confidence interval.

plot_ellipse simply plots an ellipse arround scattered points with 95% confidence interval.The code based on Ohad Gal fit_ellipse (2003)Format: handle_ellipse = plot_ellipse( x,y ) Input

Adds ellipses to the current plot

Adds ellipses to the current plot. The ellipses are specified by the semimajor axis radius, the semiminor axis radius, the orientation of the semimajor axis with an angle from the x-axis, and the

The proposed Decremental Circle Fitting Algorithm (DCFA) is applied on the tree detection problem.

This work presents an unsupervised method for tree detection from high resolution UAV imagery based on a modified version of the Decremental Ellipse Fitting Algorithm DEFA. The proposed Decremental

Draws an ellipse or arc on the current or specified axes

Draw an ellipse. If an axes object is specified, draws on that axes, otherwise draws on the current axes. Can specify x,y position and x,y radii. The y radius can be omitted to draw a circle if no

Fit a circle to a set of measured x,y points.

Fits a plane to a set of data points by minimizing the normal quadratic distance

Given a set of points (3D) this function computes the plane that fits best those points by minimizing the sum of the quadratic distances (perpendicular to the plane) between the plane and the

Fit experimental data with linear piecewise continuos function with given x-axis break points.

Fit a specified number of Gaussians to a test signal.

This function takes a 1-D, slightly noisy test signal and fits 6 Gaussians to it with the fminsearch() function. The parameters (amplitude, peak location, and width) for each Gaussian are determined

Plot an error ellipse depicting confidence interval given a covariance matrix.

% ERROR_ELLIPSE - plot an error ellipse, or ellipsoid, defining % confidence region% ERROR_ELLIPSE(C22) - Given a 2x2 covariance matrix, plot the% associated error ellipse, at the origin. It

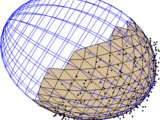
Fits a sphere to a set of noisy data. Does not require a wide arc or many points.

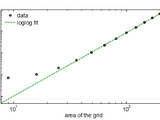
Finds and plots the linear fit to some data points when plotted on a log scale.

fit to the scaled data in a least squares sense. See the 'notes' section below for help choosing a method. logfit(X,Y), will search through all the possible axis scalings and

Model 2-d surfaces from scattered data

Fits a 2D Gaussian function to simulated data.

The program generates a 2D Gaussian. The program then attempts to fit the data using the MatLab function “lsqcurvefit “ to find the position, orientation and width of the two-dimensional

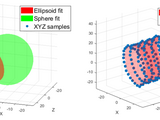
Fits an ellipsoid / sphere / paraboloid / hyperboloid to data using linear least squares.

Fits an ellipsoid or other conic surface into a 3D set of points approximating such a surface, allows some constraints, like orientation constraint and equal radii constraint. E.g., you can use it to

ELLIPSE plots an ellipse, and returns its values using 3 points selected by the user on the figure.

You can select 3 points in an existing figure or a new one, and according to your selection - you can draw an ellipse.The first 2 points are the vertices (the edges of the major / minor axis) and the

gaussian curve fit

[sigma,mu,A]=mygaussfit(x,y)[sigma,mu,A]=mygaussfit(x,y,h)this function is doing fit to the functiony=A * exp( -(x-mu)^2 / (2*sigma^2) )the fitting is been done by a polyfitthe lan of the data.h is

Draws 2D and 3D ellipses that are given in "center form".

Ellipse_plot(A,c)This function draws an N-dimensional ellipse (N = 2,3) that is given in "center form":(x - C)' A (x - C) <= 1where C is the center of the ellipse, and A is an NxN positive

Computes the perimeter of an ellipse according an infinite series scheme

This function is a small by-product of my PhD work. It computes the perimeter of an ellipse according to an infinite series scheme based on the binomial factor. The order of the series can be chosen.

Fit N-dimensional scattered points with Gaussian+constant

This function uses lsqcurvefit to fit parameters D, A, mu, sig to the R^N-->R Gaussian+constant model function, z(x) = D + A*exp( -0.5 * (x-mu).' * inv(sig) *(x-mu) ) Here A and D are unknown

Conic fit using algebraic parameters based on Levenberg-Marquardt minimization scheme.

: [ParA,RSS,iters,code] = fit_conicLMA(XY,ParAini,LambdaIni)Child functions:Residuals_ellipse, Residuals_hyperbola, AtoG( can be found from previous submissions) , JmatrixLMA (included in the main function)Input:XY:given

returns approximate cartesian coordinates of equidistant points on the circumference of an ellipse.

returns approximate cartesian coordinates of equidistant points (arc length between points is the same) on the circumference of an ellipse.

Generates the coordinates of an ellipse in 3D space and can optionally plot it.

%% Definition%% Ellipse3D generates a three row, single column vector that holds the% coordinates of an ellipse in 3D space and can optionally plot it.%% Generation of the ellipse coordinates occurs

Fits a circle to a set of data points on a plane; returns the circle center (a,b) and radius R.

This is a robust and accurate circle fit. It works well even if datapoints are observed only within a small arc. This circle fit was proposed by V. Pratt in article "Direct least-squares fitting of

Projects a set of points onto an ellipse and returns the nearest corresponding points on the ellipse

This is a modified version of an iterative algorithm published by D. Eberly.Internet publication: "Distance from a point to an ellipse in 2D" (2004) Geometric Tools, LLC, www.geometrictools.comBook

Fits a circle to a set of data points on a plane; returns the circle center (a,b) and radius R.

This is a robust and accurate circle fit. It works well even if datapoints are observed only within a small arc. This circle fit wasproposed by G. Taubin in article "Estimation Of Planar Curves

Fit a spline to noisy data

of freedom for the spline and use the method of least squares to fit the spline to the noisy data. The deegres of freedom are connected to the number of breaks (knots), so the smoothing effect is

Draws a circle or ellipse on a RGB image

Draws a circle or ellipse on a RGB image.can be used to insert circles into movies.Includes a little animation demo that demonstrates the use.

Set columns in Excel to Auto Fit

This function will set the selected columns to autofit.This is the same as using the Excel menu: Format -> Column -> AutoFit Selection .Example :xlsAutoFitCol('filename','Sheet1','A:F')

circumscribe data into an ellipse

Syntax: [ ellipseX , ellipseY ] = ellipsate( dataX , dataY , stdev ) Example: data=mvnrnd([0.5 1.5], [0.025 0.03 ; 0.03 0.16], 100); dataX=data(:,1); dataY=data(:,2); stdev = 2

Direct fitting of ellipses, ellipsoids, and hyperellipsoids

The function HYPERELLIPSOIDFIT.M fits a quadratic surface to given n-dimensional data. It has been written especially for ellipsoid fitting purposes. It contains n-dimensional elaborations of several

Plots a filled ellipse in a certain orientation using Matlab's 'patch'.

function plot_ellipse(a,b,cx,cy,angle,color)%a: width in pixels%b: height in pixels%cx: horizontal center%cy: vertical center%angle: orientation ellipse in degrees%color: color code (e.g., 'r' or

A fault-tolerant function for computing a circle's center and radius given three x-y points

following:>> ABC=[[-1 0;0 1;1 0] [-1 0;0 0;0 1]]ABC = -1 0 -1 0 0 1 0 0 1 0 0 1>> [R,xcyc] = fit_circle_through_3_points(ABC)R = 1.0000 0.7071xcyc =

A dynamic three dimensional N-body gravity simulator!

Fits a polynomial f(x,y) to best fit the data points z using SVD.

Use coeffs = fit2dPolySVD(x, y, z, order) to fit a polynomial of x and y so that it provides a best fit to the data z.Uses SVD which is robust even if the data is degenerate. Will always produce a

In the attached file example i use "nlinfit", which can fit any kind of function that you want. the

On the gaussian fit i used "polyfit" which gives you en absolut one solution, but have some problems fitting non-linear model.In the attached file example i use "nlinfit", which can fit any kind of

A baseline fit is interpolated from selected points and then applied to the data.

Baseline Fit each column in "x".There did not seem to be a similar function in th file exchange. This routine is simply a wrapper for two Matlab routines, interp1 and ginput. Syntax: [ycorr,yfit

Fit data points with different standard deviations by weighting them.

% This code fits makes a linear fit to a data set (using y =bx+a) where each data point% has a different or constant standard deviation. Your data should have three or two columns.% The first column