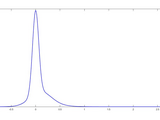
Numerical Probability Density Function from Characteristic Function
This function computes the numerical probability density function of the convolution of the Fourier Transforms of a standard mean reverting process without long term mean level and a mean reverting process presenting a jump rather than a diffusion. From such a numerical probability density function it is possible to estimate the parameter values running a standard maximum likelihood procedure. This machinery represents a good choice when modelling variables that present peaks in their distribution that fastly come back to their mean level.
The function takes as inputs the sample space, the initial values for the processes X and Y and the values of the parameters for the two considered processes. When one desires to estimate such parameters via maximum likelihood, just run the Matlab function mle, taking as input conv_pdf and the considered sample data.
Example:
x = -1:0.01:3;
init = [0 0];
param = [5 0.2 20 0.5 0.1 0.2]
Cite As
Giulio Francesca (2024). Numerical Probability Density Function from Characteristic Function (https://www.mathworks.com/matlabcentral/fileexchange/59896-numerical-probability-density-function-from-characteristic-function), MATLAB Central File Exchange. Retrieved .
MATLAB Release Compatibility
Platform Compatibility
Windows macOS LinuxCategories
- AI and Statistics > Statistics and Machine Learning Toolbox >
- Sciences > Mathematics > Probability & Statistics > Probability Density Functions >
Tags
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.
| Version | Published | Release Notes | |
|---|---|---|---|
| 1.0.0.0 | sample image inserted
|