asympPDC Package
asympPDC Package 
by Koichi Sameshima and Luiz A. Baccalá
October 05, 2022
The asympPDC Package consists of MATLAB/Octave functions and scripts collection for the analysis of multiple time series, such as EEG, biological signals and climate data, for the inference of directed interactions between structures in the frequency domain using Partial Directed Coherence (PDC) — based on the concept of Granger causality — and Directed Transfer Function (DTF), both in three metrics (Euclidean, diagonal and information) under the strict asymptotic statistics with p-values and confidence intervals also provided in the frequency domain.
Installation and usage
The asympPDC Package contains MATLAB/Octave m-files and subdirectories that you may download and copy into your local preferred working directory. To start, you should go to the package root directory and run the startup.m script in the MATLAB/Octave command line window that will set paths and check for the requirements.
>> startupBesides adding paths, startup.m will also check for the presence of required MATLAB toolboxes (Control System
Toolbox(TM), Signal Processing Toolbox(TM), and Statistics Toolbox(TM) or Statistics or Machine Learning Toolbox(TM)) or Octave packages (control, signal, and statistics). This is a standalone package that will most likely work in the recent versions of Octave — 6.3.0, 6.4.0, 7.1.0 and 7.2.0 (this latter version tested on MX Linux 32-bit). (Please report problems or suggest corrections to any issues related to compatibility with Octave).
To run all examples provided in ./examples subdirectory and verify if your installation is working properly, execute:
>> run_all_examplesIf run_all_examples.m completes successfully, congratulation, you should see 40+ overlapped figures that you could examine, in MATLAB, through
>> tilefigs1 or tilefigs2These commands tile the screen with figure windows. The tilefigs1 and tilefigs2 functions do not seem to work in the Octave environment (on Octave v7.2.0 tilefigs2 and tilefigs2 recovered function to tile the figure windows, but these windows stay behind Octave IDE).
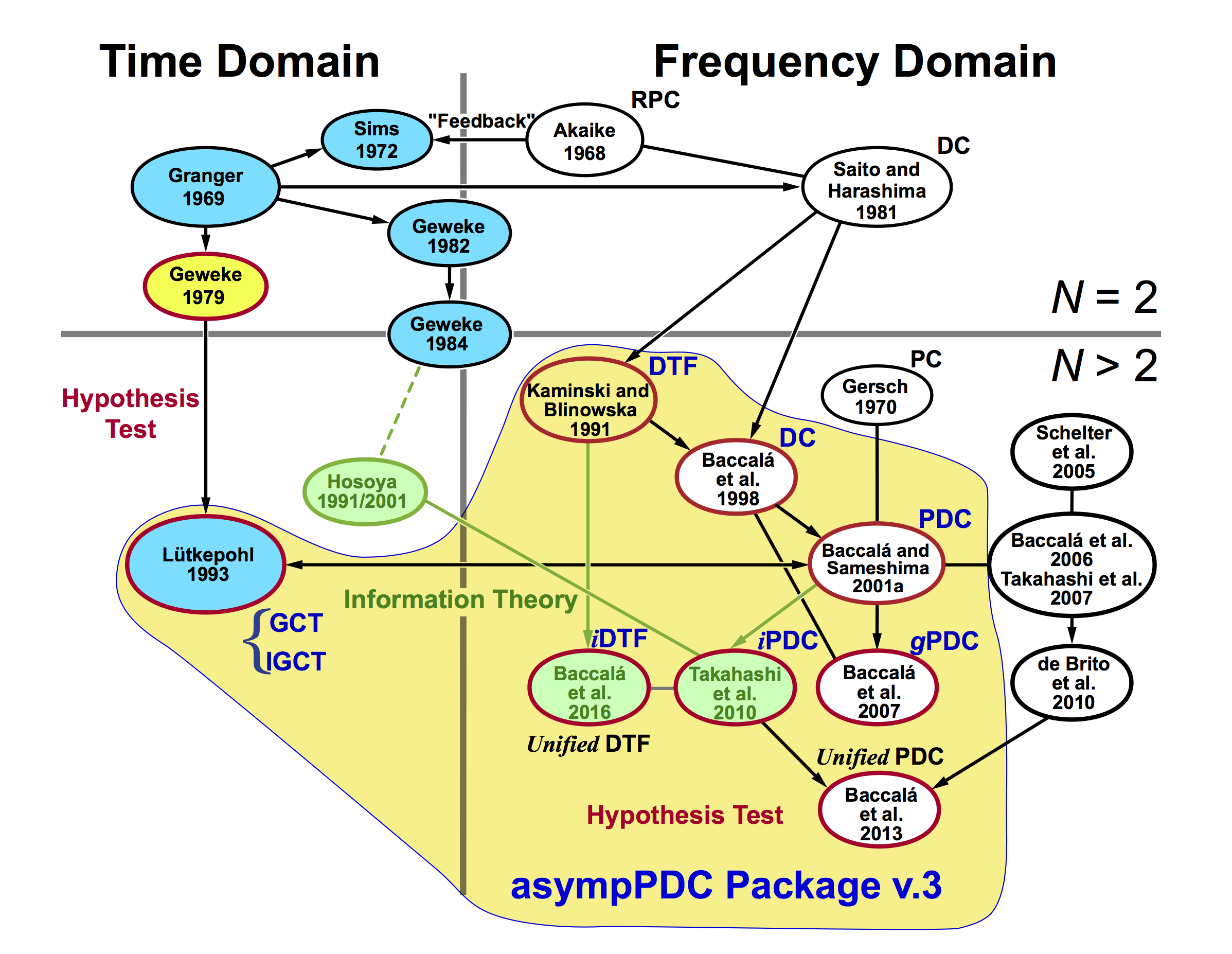
Schematic view of connectivity measures evolution
The figure bellow shows schematically the evolution path of directed connectivity, Granger causality and allied concepts developed along the last half-century from bivariate (N = 2) to multivariate (N > 2) time series, and from time domain to frequency domain analysis. The measures inside the yellow area are those implemented in asympPDC Package.
-
Legend: N - number of channels in time series; RPC - relative power contribution; DC - directed coherence or generalized directed transfer function; GCT - Granger causality test; iGCT - instantaneous Granger causality test; DTF - directed transfer function; PC - partial spectral coherence; PDC - partial directed coherence; gPDC - generalized partial directed coherence; iPDC - information partial directed coherence; iDTF - information directed transfer function.
-
Authors(sorted by year): Akaike 1968; Granger 1969; Gersch and Goddard 1970; Sims 1972; Geweke 1979; Saito and Harashima 1981; Geweke 1982; Geweke 1984; Kamiński and Blinowska 1991; Hosoya 1991; Lütkepohl 1993 --> 2005; Hosoya 2001; Baccalá et al. 1998; Baccalá and Sameshima 2001; Schelter et al. 2005; Baccalá et al. 2006; Takahashi et al. 2007; Baccalá et al. 2007; de Brito et al. 2010; Takahashi et al. 2010; Baccalá et al. 2013; Baccalá et al. 2016.
Lütkepohl, H. (1993) Introduction to Multiple Time Series Analysis. 2nd Edition, Springer, Berlin.
Saito, Y. and H. Harashima (1981) Tracking of information within multichannel record: causal analysis in EEG. In Recent Advances in EEG and EMG Data Processing. pp. 133–146, Amsterdam: Elsevier. (Hard to find !)
Getting started work flow
To get started, you may modify the analysis_template.m script file to adapt it to your needs and data sets. This template file
contains four examples of data that might be of help to deal with your
own data sets. The basic steps to set up and analyze a data set using asympPDC Package are:
-
Importing or opening column- or row-vectors data file;
-
Choosing proper label for your data, assigning values to
chLabelsvariable, or leave it empty, [ ]; -
Data pre-processing: filtering, detrending and standardization (optional);
-
Multivariate autoregressive (MAR) model estimation, by choosing parameters, estimation algorithm and model order selection criterion;
-
PDC or DTF estimation, choosing analysis parameters such as significance levels for connectivity inference (
alpha,gct_signifandigct_signif) , metric for PDC/DTF, and number of frequency points, then callasymp_pdcorasymp_dtffunction, and the analysis results will be saved in MATLABstructvariable that could be used for further analysis, or plotted; -
Visualization of analysis results through the use of
xplot,xplot_pvaluesandxplot_titlefunctions that will properly format and plot PDC/DTF and corresponding p-values results saved instruct variableobtained in the previous step in the frequency domain. Several matrix-layout plotting usingxplotandxplot_pvaluescan be achieved by properly choice of plotting parameters, i.e.flgPrinting,w_max,flgColor,flgScale,flgMax, andflgSignifColor. See further details in thexplotfunction.
Examples
Examples from the literature are provided in ./examples directory with complete m-files in program structure similar to analysis_template.m.
We hope that the examples may help readers and users to understand
and/or gain further insight into Granger causality, instantaneous
Granger causality, PDC, and DTF concepts and the realm of connectivity
analysis. Use MATLAB/Octave help command to look up more
detail of each function or script. The help itself may also provide
links to the corresponding literature materials.
We hope you enjoy it. Please give us feedback. Good luck.
References
A. The asympPDC Package implementation is based mainly on the following articles and books:
A. The asympPDC Package implementation is based mainly on the following articles and books
[1] L.A. Baccalá and K. Sameshima (2001). Partial directed coherence: a new concept in neural structure determination. Biol Cybern 84:463–474. https://doi.org/10.1007/PL00007990
[2] D.Y. Takahashi, L.A. Baccalá and K. Sameshima (2007), Connectivity inference between neural structures via partial directed coherence. J Appl Stat 34:1259–1273. https://doi.org/10.1080/02664760701593065
[3] L.A. Baccalá, C.S.N. De Brito, D.Y. Takahashi and K. Sameshima (2013). Unified asymptotic theory for all partial directed coherence forms. Philos T Roy Soc A 371:1–13. https://doi.org/10.1098/rsta.2012.0158
[4] M.J. Kamiński and K.J. Blinowska (1991). A new method of the description of the information flow in the brain structures. Biol Cybern 65:203–210. https://doi.org/10.1007/bf00198091
[5] L.A. Baccalá, D.Y. Takahashi and K. Sameshima (2016). Directed transfer function: unified asymptotic theory and some of its implications. IEEE T Bio-Med Eng 63:2450–2460. https://doi.org/10.1109/TBME.2016.2550199
[6] H. Lütkepohl (2005). New Introduction to Multiple Time Series Analysis. Springer-Verlag, Berlin. https://doi.org/10.1007/978-3-540-27752-1
[7] S.L. Marple Jr (1987). Digital Spectral Analysis with Application. Prentice-Hall, Englewood-Cliffs.
[8] T. Schneider and A. Neumaier (2001). Algorithm 808: ARfit - A Matlab package for the estimation of parameters and eigenmodes of multivariate autoregressive models. ACM Trans Math Softw 27:58–65. https://doi.org/10.1145/382043.382316
[9] K. Sameshima and L.A. Baccalá Eds. (2014). Methods in Brain Connectivity Inference through Multivariate Time Series Analysis. CRC Press, Boca Raton. https://doi.org/10.1201/b16550
B. Historical development: Biological Cybernetics 60th ANNIVERSARY RETROSPECTIVE
[10] L.A. Baccalá and K. Sameshima (2021). Partial directed coherence: twenty years on some history and an appraisal. Biol Cybern 115:195–204. https://doi.org/10.1007/s00422-021-00880-y
C. Things to come: Total PDC/DTF with asymptotic statistics, spectral factorization and faster PDC/DTF estimation algorithms . . .
[11] L.A. Baccalá and K. Sameshima (2021). Frequency domain repercussions of instantaneous Granger causality. Entropy 23:10.3390/e23081037 https://doi.org/10.3390/e23081037
[12] L.A. Baccalá and K. Sameshima (2022). Partial directed coherence and the vector autoregressive modelling myth and a
caveat. Front Netw Physiol 2:845327. https://doi.org/10.3389/fnetp.2022.845327 (Note: MATLAB/Octave scripts and functions used to generate all four figures of this article are provided in ./demo/PDCVARMYTH2022 subdirectory. To use follow the instructions in Readme file.)
License
These routines are distributed under GNU General Public License v3.0 under authorship of Koichi Sameshima and Luiz A. Baccalá - July 2022.
Cite as
Koichi Sameshima and Luiz A. Baccalá (2022). asympPDC Package (Release v3.0), GitHub. Retrieved August 12, 2022.
MATLAB Release Compatibility
Platform Compatibility
Windows macOS LinuxCategories
Tags
Community Treasure Hunt
Find the treasures in MATLAB Central and discover how the community can help you!
Start Hunting!Discover Live Editor
Create scripts with code, output, and formatted text in a single executable document.
demo/PDCVARMYTH2022
demo/PDCVARMYTH2022/others
examples
examples/models
utils
utils/arfit
utils/legacy
core
demo/PDCVARMYTH2022
examples
extras
utils
| Version | Published | Release Notes | |
|---|---|---|---|
| 3.0.6.4 | See release notes for this release on GitHub: https://github.com/asymppdc/asympPDC/releases/tag/v3.0.6.4 |
||
| 3.0.6.3 | See release notes for this release on GitHub: https://github.com/asymppdc/asympPDC/releases/tag/v3.0.6.3 |
||
| 3.0.5 | See release notes for this release on GitHub: https://github.com/asymppdc/asympPDC/releases/tag/v3.0.5 |
||
| 3.0.3 | See release notes for this release on GitHub: https://github.com/asymppdc/asympPDC/releases/tag/v3.0.3 |
||
| 3.0.2 | |||
| 3.0.1.0 | See release notes for this release on GitHub: https://github.com/asymppdc/asympPDC/releases/tag/v3.0.1 |
||
| 3.0.0.1 | See release notes for this release on GitHub: https://github.com/asymppdc/asympPDC/releases/tag/v3.0.0.1 |