Use Symbolic Objects to Represent Mathematical Objects
To solve mathematical problems with Symbolic Math Toolbox™, you can define symbolic objects to represent various mathematical objects. This example discusses the usage of these symbolic objects in the Command Window:
symbolic number
symbolic scalar variable, function, and expression
symbolic equation
symbolic vector and matrix
symbolic matrix variable
symbolic matrix function
Symbolic Number
Defining a number as a symbolic number instructs MATLAB® to treat the number as an exact form instead of using a numeric approximation. For example, use a symbolic number to represent the argument of an inverse trigonometric function .

Create the symbolic number using sym, and assign it to
a.
a = sym(1/sqrt(2))
a = 2^(1/2)/2
Find the inverse sine of a. The result is the symbolic number
pi/4.
thetaSym = asin(a)
thetaSym = pi/4
You can convert a symbolic number to variable-precision arithmetic by using vpa. The result is a decimal number with 32 significant
digits.
thetaVpa = vpa(thetaSym)
thetaVpa = 0.78539816339744830961566084581988
To convert the symbolic number to a double-precision number, use
double. For more information about whether to use numeric or
symbolic arithmetic, see Choose Numeric or Symbolic Arithmetic.
thetaDouble = double(thetaSym)
thetaDouble = 0.7854
Symbolic Scalar Variable, Function, and Expression
Defining variables, functions, and expressions as symbolic objects enables you to perform algebraic operations with those symbolic objects, including simplifying formulas and solving equations. For example, use a symbolic scalar variable, function, and expression to represent the quadratic function . For brevity, a symbolic scalar variable is also called a symbolic variable.

Create a symbolic scalar variable x using syms. You can also use sym to create a symbolic scalar variable. For more information about
whether to use syms or sym, see Choose syms or sym Function.
Define a symbolic expression
x^2 + x - 2 to represent the right side of the quadratic equation and
assign it to f(x). The identifier f(x) now refers
to a symbolic function that represents the quadratic function. A
symbolic function accepts scalars as input
arguments.
syms x f(x) = x^2 + x - 2
f(x) = x^2 + x -2
You can then evaluate the quadratic function by providing its input argument inside
the parentheses. For example, evaluate
f(2).
fVal = f(2)
fVal = 4
You can also solve the quadratic equation . Use solve to find the roots of the quadratic
equation. solve returns the two solutions as a vector of two symbolic
numbers.
sols = solve(f)
sols = -2 1
Symbolic Equation
Defining a mathematical equation as a symbolic equation enables you to find the solution of the equation. For example, use a symbolic equation to solve the trigonometric problem .
![]()
Create a symbolic function g(t) using syms.
Assign the symbolic expression 2*sin(t)*cos(t) to
g(t).
syms g(t) g(t) = 2*sin(t)*cos(t)
g(t) = 2*cos(t)*sin(t)
== operator and assign the mathematical
relation g(t) == 1 to eqn. The identifier
eqn is a symbolic equation that represents the trigonometric
problem.eqn = g(t) == 1
eqn = 2*cos(t)*sin(t) == 1
Use solve to find the solution of the trigonometric
problem.
sol = solve(eqn)
sol = pi/4
Symbolic Vector and Matrix
Use a symbolic vector and matrix to represent and solve a system of linear equations.
You can represent the system of equations as a vector of two symbolic equations. You can also represent the system of equations as a matrix problem involving a matrix of symbolic numbers and a vector of symbolic variables. For brevity, any vector of symbolic objects is called a symbolic vector and any matrix of symbolic objects is called a symbolic matrix.
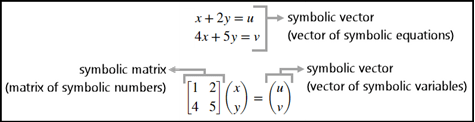
Create two symbolic equations eq1 and eq2.
Combine the two equations into a symbolic
vector.
syms u v x y eq1 = x + 2*y == u; eq2 = 4*x + 5*y == v; eqns = [eq1, eq2]
eqns = [x + 2*y == u, 4*x + 5*y == v]
Use solve to find the solutions of the system of equations
represented by eqns. solve returns a structure
S with fields named after each of the variables in the equations.
You can access the solutions using dot notation, as S.x and
S.y.
S = solve(eqns); S.x
ans = (2*v)/3 - (5*u)/3
S.y
ans = (4*u)/3 - v/3
Another way to solve the system of linear equations is to convert it to matrix form.
Use equationsToMatrix to convert the system of equations to matrix
form and assign the output to A and b. Here,
A is a symbolic matrix and b is a symbolic
vector. Solve the matrix problem by using the matrix division \
operator.
[A,b] = equationsToMatrix(eqns,x,y)
A = [1, 2] [4, 5] b = u v
sols = A\b
sols =
(2*v)/3 - (5*u)/3
(4*u)/3 - v/3Symbolic Matrix Variable
Since R2021a
Use symbolic matrix variables to evaluate differentials with respect to vectors.
Symbolic matrix variables represent matrices, vectors, and scalars in compact matrix notation. Symbolic matrix variables offer a concise display in typeset and show mathematical formulas with more clarity. You can enter vector- and matrix-based expressions as symbolic matrix variables in Symbolic Math Toolbox.

Create three symbolic matrix variables x, y, and
A using the syms command with the
matrix syntax. Nonscalar symbolic matrix variables are displayed
as bold characters in the Command Window and in the Live
Editor.
syms x [4 1] matrix syms y [3 1] matrix syms A [3 4] matrix x y A
x = x y = y A = A
alpha. Find the differential of alpha with
respect to the vectors x and y that are represented by the symbolic matrix variables
x and
y.alpha = y.'*A*x
alpha = y.'*A*x
Dx = diff(alpha,x)
Dx = y.'*A
Dy = diff(alpha,y)
Dy = x.'*A.'
[1; 2; 3] in Dx and
substitute x with [-1; 2; 0; 1] in Dy using
subs. When evaluating a symbolic expression, you must substitute
values that have the same size as the defined symbolic matrix
variables.Dx = subs(Dx,y,[1; 2; 3])
Dx = symmatrix([1;2;3]).'*A
Dy = subs(Dy,x,[-1; 2; 0; 1])
Dx = symmatrix([-1;2;0;1]).'*A.'
Symbolic Matrix Function
Since R2022a
Use a symbolic matrix function to evaluate a matrix polynomial.
A symbolic matrix function represents a parameter-dependent function that accepts matrices, vectors, and scalars as input arguments. Symbolic matrix function operates on matrices in compact matrix notation, offering a concise display in typeset and showing mathematical formulas with more clarity. You can enter vector- and matrix-based formulas as symbolic matrix functions in Symbolic Math Toolbox.

Create a 2-by-2 symbolic matrix variable A using the
syms command with the matrix syntax. Create a
symbolic matrix function f(A) that accepts A as an
input argument using the syms command with the matrix
keepargs syntax to keep the previous definition of
A.
syms A 2 matrix syms f(A) 2 matrix keepargs
f(A) = A^2 - 3*A + 2*eye(2)
f(A) = 2*symmatrix(eye(2)) - 3*A + A^2
A = [1 2; -2 -1]. When evaluating a
symbolic matrix function, you must substitute values that have the same size as the
defined input
arguments.fEval = f([1 2; -2 -1])
fEval = - 3*symmatrix([1,2;-2,-1]) + symmatrix([1,2;-2,-1])^2 + 2*symmatrix(eye(2))
symmatrix data type to the
sym data
type.fSym = symmatrix2sym(fEval)
fSym = [-4, -6] [ 6, 2]
Comparison of Symbolic Objects
This table compares the symbolic objects that are available in Symbolic Math Toolbox.
| Symbolic Object | Examples of MATLAB Command | Size of Symbolic Object | Data Type |
|---|---|---|---|
| Symbolic number |
a = 1/sqrt(sym(2)) theta = asin(a) a = 2^(1/2)/2 theta = pi/4 | 1-by-1 | sym |
| Symbolic scalar variable |
syms x y u v | 1-by-1 | sym |
| Symbolic function |
syms x f(x) = x^2 + x - 2 syms g(t) [1 3] g f(x) = x^2 + x - 2 g(t) = [g1(t), g2(t), g3(t)] |
|
|
| Symbolic expression |
syms x expr = x^2 + x - 2 expr2 = 2*sin(x)*cos(x) expr = x^2 + x - 2 expr2 = 2*cos(x)*sin(x) | 1-by-1 | sym |
| Symbolic equation |
syms u v x y eq1 = x + 2*y == u eq2 = 4*x + 5*y == v eq1 = x + 2*y == u eq2 = 4*x + 5*y == v | 1-by-1 | sym |
| Symbolic vector |
syms u v b = [u v] b = [u, v] | 1-by-n or
m-by-1, where
m is the row size and n is the
column size | sym |
| Symbolic matrix |
syms A x y A = [x y; x*y y^2] A = [ x, y] [x*y, y^2] | m-by-n, where
m is the row size and n is the
column size | sym |
| Symbolic multidimensional array |
syms A [2 1 2] A A(:,:,1) = A1_1 A2_1 A(:,:,2) = A1_2 A2_2 | sz1-by-sz2-...-szn,
where szn is the size of the nth
dimension | sym |
Symbolic matrix variable (since R2021a) |
syms A B [2 3] matrix A B A = A B = B | m-by-n, where
m is the row size and n is the
column size | symmatrix |
Symbolic matrix function (since R2022a) |
syms X Y [2 2] matrix syms f(X,Y) [2 2] matrix keepargs f(X,Y) = X*Y - Y*X f(X, Y) = X*Y - Y*X |
|
|
See Also
syms | sym | symfun | symmatrix | symfunmatrix | symfunmatrix2symfun | symmatrix2sym | str2sym