Solve a Second-Order Differential Equation Numerically
This example shows you how to convert a second-order differential equation into a system of differential equations that can be solved using the numerical solver ode45 of MATLAB®.
A typical approach to solving higher-order ordinary differential equations is to convert them to systems of first-order differential equations, and then solve those systems. The example uses Symbolic Math Toolbox™ to convert a second-order ODE to a system of first-order ODEs. Then it uses the MATLAB solver ode45 to solve the system.
Rewrite the Second-Order ODE as a System of First-Order ODEs
Use odeToVectorField to rewrite this second-order differential equation
using a change of variables. Let and such that differentiating both equations we obtain a system of first-order differential equations.
syms y(t)
[V] = odeToVectorField(diff(y, 2) == (1 - y^2)*diff(y) - y)V =
Generate MATLAB Function
The MATLAB ODE solvers do not accept symbolic expressions as an input. Therefore, before you can use a MATLAB ODE solver to solve the system, you must convert that system to a MATLAB function. Generate a MATLAB function from this system of first-order differential equations using matlabFunction with V as an input.
M = matlabFunction(V,'vars', {'t','Y'})
M = function_handle with value:
@(t,Y)[Y(2);-(Y(1).^2-1.0).*Y(2)-Y(1)]
Solve the System of First-Order ODEs
To solve this system, call the MATLAB ode45 numerical solver using the generated MATLAB function as an input.
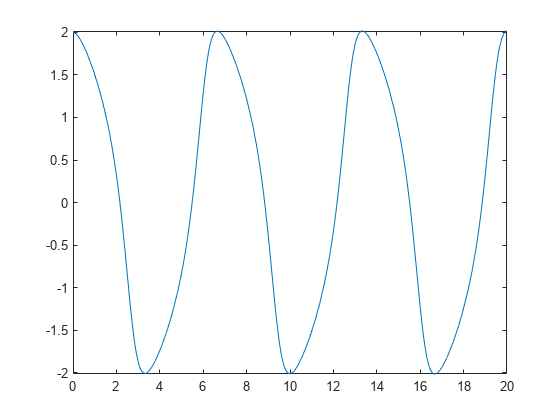
sol = ode45(M,[0 20],[2 0]);
Plot the Solution
Plot the solution using linspace to generate 100 points in the interval [0,20] and deval to evaluate the solution for each point.
fplot(@(x)deval(sol,x,1), [0, 20])