Limits
The fundamental idea in calculus is to make calculations on functions as a variable “gets close to” or approaches a certain value. Recall that the definition of the derivative is given by a limit
provided this limit exists. Symbolic Math Toolbox™ software enables you to calculate the limits of functions directly. The commands
syms h n x limit((cos(x+h) - cos(x))/h, h, 0)
which return
ans = -sin(x)
and
limit((1 + x/n)^n, n, inf)
which returns
ans = exp(x)
illustrate two of the most important limits in mathematics: the derivative (in this case of cos(x)) and the exponential function.
One-Sided Limits
You can also calculate one-sided limits with Symbolic Math Toolbox software. For example, you can calculate the limit of x/|x|, whose graph is shown in the following figure, as x approaches 0 from the left or from the right.
syms x fplot(x/abs(x), [-1 1], 'ShowPoles', 'off')
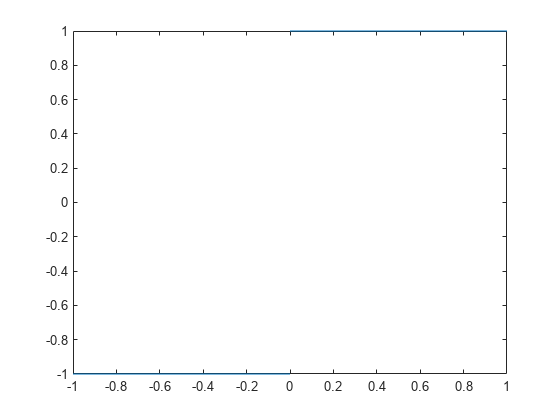
To calculate the limit as x approaches 0 from the left,
enter
syms x limit(x/abs(x), x, 0, 'left')
ans = -1
To calculate the limit as x approaches 0 from the right,
enter
syms x limit(x/abs(x), x, 0, 'right')
ans = 1
Since the limit from the left does not equal the limit from the right, the two- sided
limit does not exist. In the case of undefined limits, MATLAB® returns NaN (not a number). For example,
syms x limit(x/abs(x), x, 0)
returns
ans = NaN
Observe that the default case, limit(f) is the same as
limit(f,x,0). Explore the options for the
limit command in this table, where f is a
function of the symbolic object x.
Mathematical Operation | MATLAB Command |
|---|---|
| |
| |
| |
|