Interactive Calculus in Live Editor

Adding Interactive Controls to Your Script

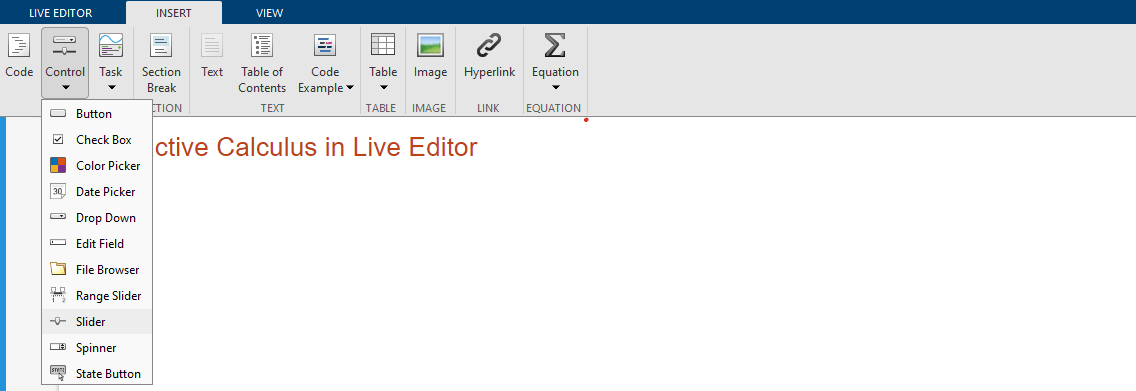
An interactive control can be used to change the values of variables in your live script. To add a numeric slider, go to the Insert tab, click the Control button, and select Slider. For more information, see Add Interactive Controls to a Live Script.

Initialize Variables and Function

Evaluate the integral

using Riemann sum approximation.

A Riemann sum is a numerical approximation of the analytical integration by a finite sum of rectangular areas. Use the interactive slider bars to set the upper bound of the integral, the number of rectangles, and the constant factor of the function.

syms x;
xMax = 4;
numRectangles = 30;
c = 2.5;
f(x) = c*x^2;
yMax = double(f(xMax));

Visualize the Area Under the Curve Using Riemann Sums

Plot the integrand f.

fplot(f);
xlim([0 xMax]); ylim([0 yMax]);
legend({},Location="north",FontSize=20);
title("Riemann Sum",FontSize=20);

Calculate the rectangular areas that approximate the area under the curve of the integral. Plot the rectangles.

width = xMax/numRectangles;
sum = 0;
for i = 0:numRectangles-1
    xval = i*width;
    height = double(f(xval));
    rectangle(Position=[xval 0 width height],EdgeColor="r");
    sum = sum + width*height;
end
text(xMax/10,yMax/3,["Area = " num2str(sum)],FontSize=20);

Calculate the Integral Analytically

Calculate the integral analytically. Use vpa to numerically approximate the exact symbolic result to 32 significant digits.

fInt = int(f,0,xMax)

fInt = 
$$\frac{160}{3}$$

vpa(fInt)

ans = $$53.333333333333333333333333333333$$