Integration
If f is a symbolic expression, then
int(f)
attempts to find another symbolic expression, F, so that
diff(F) = f. That is,
int(f) returns the indefinite integral or antiderivative of
f (provided one exists in closed form). Similar to
differentiation,
int(f,v)
uses the symbolic object v as the variable of integration, rather than
the variable determined by symvar. See how int works by
looking at this table.
Mathematical Operation | MATLAB® Command |
|---|---|
| |
| |
g = cos(at + b) |
|
|
In contrast to differentiation, symbolic integration is a more complicated task. A number of difficulties can arise in computing the integral:
The antiderivative,
F, may not exist in closed form.The antiderivative may define an unfamiliar function.
The antiderivative may exist, but the software can't find it.
The software could find the antiderivative on a larger computer, but runs out of time or memory on the available machine.
Nevertheless, in many cases, MATLAB can perform symbolic integration successfully. For example, create the symbolic variables
syms a b theta x y n u z
The following table illustrates integration of expressions containing those variables.
f | int(f) |
|---|---|
syms x n f = x^n; |
int(f) ans = piecewise(n == -1, log(x), n ~= -1,... x^(n + 1)/(n + 1)) |
syms y f = y^(-1); |
int(f) ans = log(y) |
syms x n f = n^x; |
int(f) ans = n^x/log(n) |
syms a b theta f = sin(a*theta+b); |
int(f) ans = -cos(b + a*theta)/a |
syms u f = 1/(1+u^2); |
int(f) ans = atan(u) |
syms x f = exp(-x^2); |
int(f) ans = (pi^(1/2)*erf(x))/2 |
In the last example, exp(-x^2), there is no formula for the integral
involving standard calculus expressions, such as trigonometric and exponential functions. In
this case, MATLAB returns an answer in terms of the error function erf.
If MATLAB is unable to find an answer to the integral of a function f,
it just returns int(f).
Definite integration is also possible.
Definite Integral | Command |
|---|---|
|
|
|
|
Here are some additional examples.
f | a, b | int(f, a, b) |
|---|---|---|
syms x f = x^7; |
a = 0; b = 1; |
int(f, a, b) ans = 1/8 |
syms x f = 1/x; |
a = 1; b = 2; |
int(f, a, b) ans = log(2) |
syms x f = log(x)*sqrt(x); |
a = 0; b = 1; |
int(f, a, b) ans = -4/9 |
syms x f = exp(-x^2); |
a = 0; b = inf; |
int(f, a, b) ans = pi^(1/2)/2 |
syms z f = besselj(1,z)^2; |
a = 0; b = 1; |
int(f, a, b) ans =
hypergeom([3/2, 3/2],...
[2, 5/2, 3], -1)/12 |
For the Bessel function (besselj) example, it is possible to compute a
numerical approximation to the value of the integral, using the double function. The commands
syms z a = int(besselj(1,z)^2,0,1)
return
a = hypergeom([3/2, 3/2], [2, 5/2, 3], -1)/12
and the command
a = double(a)
returns
a =
0.0717Integration with Real Parameters
One of the subtleties involved in symbolic integration is the “value” of various parameters. For example, if a is any positive real number, the expression
is the positive, bell shaped curve that tends to 0 as x tends to ±∞. You can create an example of this curve, for a = 1/2.
syms x
a = sym(1/2);
f = exp(-a*x^2);
fplot(f)
However, if you try to calculate the integral
without assigning a value to a, MATLAB assumes that a represents a complex number, and therefore
returns a piecewise answer that depends on the argument of a. If you are
only interested in the case when a is a positive real number, use
assume to set an assumption on a:
syms a assume(a > 0)
Now you can calculate the preceding integral using the commands
syms x f = exp(-a*x^2); int(f, x, -inf, inf)
This returns
ans = pi^(1/2)/a^(1/2)
Integration with Complex Parameters
To calculate the integral
for complex values of a, enter
syms a x f = 1/(a^2 + x^2); F = int(f, x, -inf, inf)
Use syms to clear all the assumptions on variables. For more
information about symbolic variables and assumptions on them, see Use Assumptions on Symbolic Variables.
The preceding commands produce the complex output
F = (pi*signIm(1i/a))/a
The function signIm is defined as:
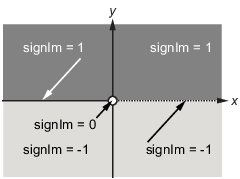
To evaluate F at a = 1 + i, enter
g = subs(F, 1 + i)
g = pi*(1/2 - 1i/2)
double(g)
ans = 1.5708 - 1.5708i
High-Precision Numerical Integration Using Variable-Precision Arithmetic
High-precision numerical integration is implemented in the vpaintegral function of the Symbolic Math Toolbox™. vpaintegral uses variable-precision arithmetic in
contrast to the MATLAB
integral function, which uses
double-precision arithmetic.
Integrate besseli(5,25*u).*exp(-u*25) by using both
integral and vpaintegral. The
integral function returns NaN and issues a
warning while vpaintegral returns the correct result.
syms u f = besseli(5,25*x).*exp(-x*25); fun = @(u)besseli(5,25*u).*exp(-u*25); usingIntegral = integral(fun, 0, 30) usingVpaintegral = vpaintegral(f, 0, 30)
Warning: Infinite or Not-a-Number value encountered. usingIntegral = NaN usingVpaintegral = 0.688424
For more information, see vpaintegral.
See Also
int | diff | vpaintegral