Hilbert Matrices and Their Inverses
This example shows how to compute the inverse of a Hilbert matrix using Symbolic Math Toolbox™.
Definition : A Hilbert matrix is a square matrix with entries being the unit fraction. . For example, the 3x3 Hilbert matrix is
Symbolic computations give accurate results for these ill-conditioned matrices, while purely numerical methods fail.
Create a 20-by-20 numeric Hilbert matrix.
H = hilb(20);
Find the condition number of this matrix. Hilbert matrices are ill-conditioned, meaning that they have large condition numbers indicating that such matrices are nearly singular. Note that computing condition numbers is also prone to numeric errors.
cond(H)
ans = 2.1065e+18
Therefore, inverting Hilbert matrices is numerically unstable. When you compute a matrix inverse, H*inv(H) must return an identity matrix or a matrix close to the identity matrix within some error margin.
First, compute the inverse of H by using the inv function. A warning is thrown due to the numerical instability.
H*inv(H)
Warning: Matrix is close to singular or badly scaled. Results may be inaccurate. RCOND = 9.542396e-20.
ans = 20×20
1.0000 -0.0000 -0.0003 0.0044 0.0212 -0.2436 0.4383 -0.6683 -0.4409 0.6464 -0.9986 -0.4477 8.3067 -0.2302 -0.4680 -0.4770 1.4327 -1.4875 8.0000 2.0000
0.4314 1.0000 -0.0002 0.0003 0.0528 -0.0284 0.9397 0.6603 -0.1158 1.3085 -0.5132 0.2835 0.5888 -1.7213 0.7195 -1.7957 0.6355 2.8214 -8.0000 2.0000
0.7987 -0.8048 0.9997 -0.0041 0.1027 0.1222 0.5629 -0.1333 0.5837 1.0126 -0.9596 0.1601 -0.3606 -2.5592 0.5373 -2.9668 -0.2067 3.8693 -8.0000 0
1.0486 -1.6648 0.4041 0.9885 0.0958 -0.1427 1.3149 0.2797 -0.1724 0.8018 -0.1066 0.3468 5.6058 -2.5304 2.5296 -3.6839 -0.4191 3.5598 -16.0000 1.0000
1.2164 -2.4406 1.0946 -0.1853 1.1204 -0.1147 1.2598 -0.9847 0.2424 -0.0230 0.5197 0.8731 3.8277 -4.7249 0.5983 -2.3525 -0.3189 3.4062 -4.0000 3.0000
1.3286 -3.1054 1.9447 -0.5911 0.1962 0.8550 1.2190 -1.0755 0.2927 1.1158 0.2254 0.9657 3.0420 -2.0190 1.2346 -1.7681 -0.4577 3.5038 0 0
1.4027 -3.6617 2.8529 -1.1814 0.3594 -0.2091 2.4910 -0.4949 0.6416 0.4732 0.2943 -0.5944 4.9283 -4.1578 1.6593 -3.0688 -0.1768 4.6058 0 2.0000
1.4501 -4.1206 3.7522 -1.8860 0.5367 0.0995 0.2101 1.4302 -1.0067 1.5837 -1.5936 3.3039 -0.4865 0.0223 0.9902 -1.7856 -0.3147 2.2500 0 0
1.4784 -4.4954 4.6045 -2.6478 0.8130 0.1115 0.0798 0.1202 1.1006 0.0361 -0.2599 3.4626 -0.4334 -0.7285 -0.3979 0.2157 0.6016 0.2411 0 -1.0000
1.4930 -4.7986 5.3893 -3.4322 1.1685 -0.0259 0.4050 -0.0399 1.2269 0.7081 0.0601 0.9479 3.7747 -2.1672 1.9212 -1.5514 0.2045 2.7134 -4.0000 0
1.4975 -5.0417 6.0972 -4.1834 1.4561 0.0771 0.5520 0.5281 -0.6765 -0.0921 0.7289 3.0746 -0.6345 0.4550 -0.3803 0.3295 0.9800 -1.4188 0 -2.0000
1.4946 -5.2346 6.7274 -4.9048 1.7749 -0.0877 0.2437 0.2317 -0.2408 0.4926 -0.4823 1.3380 0.1269 -0.8290 1.0542 -1.0679 0.4138 0.2460 4.0000 0
1.4863 -5.3854 7.2827 -5.5776 2.1172 -0.0469 0.6250 -0.6250 0.3750 0.4062 0.1250 -0.2500 3.5000 -2.5000 1.1250 -0.5000 -0.5312 2.7500 8.0000 0
1.4740 -5.5013 7.7675 -6.1883 2.4591 -0.2935 1.0419 -0.5056 0.8891 0.4459 0.1519 -2.2266 4.4263 -3.3728 2.6915 -2.1445 -0.8045 3.5795 0 0
1.4587 -5.5879 8.1875 -6.7353 2.6649 0.0763 -0.5718 0.7748 -0.3322 -0.2596 0.1983 1.3305 -3.3098 -0.4367 -0.3577 1.1951 0.2617 -0.9577 0 0
⋮
Now, use the MATLAB® invhilb function that offers better accuracy for Hilbert matrices. This function finds exact inverses of Hilbert matrices up to 15-by-15. For a 20-by-20 Hilbert matrix, invhilb finds the approximation of the matrix inverse.
H*invhilb(20)
ans = 20×20
1010 ×
0.0000 -0.0000 0.0000 -0.0000 0.0000 -0.0004 0.0013 -0.0037 0.0047 -0.2308 0.4019 0.2620 -0.4443 -7.5099 3.4753 3.2884 -1.1618 0.2301 0.4295 0.0537
-0.0000 0.0000 -0.0000 0.0000 -0.0000 -0.0001 -0.0009 0.0172 -0.0628 0.1251 -0.8975 2.7711 -2.8924 -1.4888 -2.5102 6.4897 -3.0581 0.7925 0 -0.0268
0.0000 0.0000 0.0000 -0.0000 -0.0000 -0.0001 0.0009 0.0042 -0.0303 0.0271 -0.1028 0.2862 -0.9267 -4.0597 1.8194 4.7727 -1.3255 0.4667 0.2147 -0.0268
0.0000 0.0000 -0.0000 -0.0000 0.0000 -0.0001 0.0004 0.0002 -0.0056 0.0526 -0.1136 0.3616 -1.6920 -3.7214 0.2709 4.4169 -1.1602 0.5541 0 -0.0268
-0.0000 0.0000 -0.0000 0.0000 -0.0000 -0.0000 -0.0006 0.0068 -0.0394 0.1449 -0.7818 1.9314 -2.1273 -1.0745 -2.2988 4.6349 -1.8923 0.3793 0.2147 0.0537
0.0000 -0.0000 0.0000 -0.0000 0.0000 -0.0002 0.0014 -0.0028 0.0304 -0.1053 -0.0724 -0.2073 -0.3769 -5.0729 2.7552 2.3488 -0.5046 0.2240 0 0
-0.0000 0.0000 -0.0000 0.0000 -0.0000 0.0000 -0.0013 0.0101 -0.0520 0.1307 -0.7715 2.9297 -3.3374 1.4084 -3.8703 7.1053 -2.7578 0.8815 -0.2147 0
0.0000 -0.0000 0.0000 -0.0000 -0.0000 -0.0002 0.0018 -0.0040 0.0231 -0.0892 0.2000 0.2766 -0.8262 -4.7229 1.6513 2.1857 -0.4749 -0.1747 0 0
-0.0000 0.0000 -0.0000 0.0000 -0.0000 0.0000 0.0004 0.0144 -0.0513 0.1165 -0.7063 1.9776 -2.0602 -1.0763 -3.2081 3.8539 -2.4580 0.5675 0 0.0268
0.0000 0.0000 0.0000 -0.0000 0.0000 -0.0002 0.0008 -0.0019 0.0027 -0.0167 -0.0497 0.8865 -0.6720 -1.2729 0.0571 2.3625 -1.2616 0.2443 0.2147 0
-0.0000 0.0000 -0.0000 0.0000 -0.0000 -0.0001 0.0004 0.0050 -0.0400 0.0368 -0.4875 1.2090 -1.1395 -0.8712 -0.3376 3.4449 -1.6401 0.3319 -0.2147 0.0268
0.0000 0.0000 0.0000 -0.0000 0.0000 -0.0001 0.0009 -0.0015 -0.0172 0.0267 -0.1909 0.1515 -0.2069 -2.4186 -0.1889 3.6202 -0.9900 0.3459 -0.2147 -0.0268
-0.0000 0.0000 -0.0000 0.0000 -0.0000 -0.0000 0.0007 0.0097 -0.0384 0.0201 -0.3053 1.3925 -2.2012 -1.1811 -0.7248 3.8588 -1.6106 0.5679 -0.2147 0
0.0000 -0.0000 -0.0000 -0.0000 -0.0000 -0.0001 0.0007 0.0020 -0.0014 -0.0255 -0.1178 0.7277 -0.7834 -2.9257 1.2532 2.2557 -0.7382 0.3044 0 -0.0134
-0.0000 0.0000 -0.0000 -0.0000 -0.0000 -0.0001 0.0000 0.0043 -0.0304 0.0353 -0.3375 0.7563 -1.3325 -2.0856 -1.4510 3.1561 -1.1128 0.4057 0.2147 0
⋮
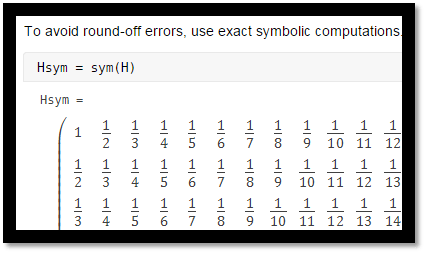
To avoid round-off errors, use exact symbolic computations. For this, create the symbolic Hilbert matrix.
Hsym = sym(H)
Hsym =
Get the value of the condition number. It has been derived by symbolic methods and is free of numerical errors.
vpa(cond(Hsym))
ans =
Although its condition number is large, you can compute the exact inverse of the matrix.
Hsym*inv(Hsym)
ans =