Handling Large Integers to Solve the 196 Problem
This example shows how to work with large integers and their decimal representation using the Symbolic Math Toolbox™.
Palindromes
A character string is called a palindrome if it is the same when read backward. A positive integer is called a palindrome if its decimal representation is a palindrome. For example, 191, 313 and 5885 are all palindromes.
Consider the following algorithm
Start with any positive integer and add it to its mirror image.
Repeat this step with the resulting number until you obtain a palindrome.
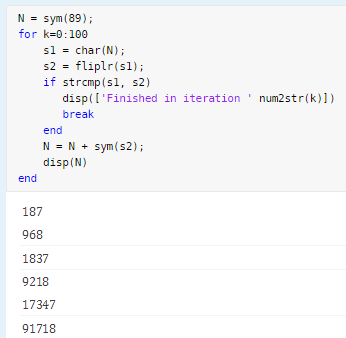
For example, choose N=89. The first 3 iterations of adding the number to its mirror image give
Eventually, after 24 iterations, you would arrive at the palindrome 8813200023188.
N = sym(89); for k=0:100 s1 = char(N); s2 = fliplr(s1); if strcmp(s1, s2) disp(['Finished in iteration ' num2str(k)]) break end N = N + sym(s2); disp(N) end
Finished in iteration 24
The 196-Problem
Does the algorithm terminate for every ?
The problem is still open, and palindrome aficionados have invested many CPU years into the case which gave the problem its name. In order to play with this problem in MATLAB®, symbolic integers are useful because their size is unlimited. Use the function sym to convert strings of decimal digits to symbolic integers, and char (not num2str) to convert back.
Investigating the famous case produces truly huge numbers. To see how many decimal digits an integer has, simply use log10.
N = sym(196); for k=0:1000 s1 = char(N); s2 = fliplr(s1); N = N + sym(s2); end disp(['Number of digits after ' num2str(k) ' iterations: ' char(ceil(log10(N)))]);
Number of digits after 1000 iterations: 411