Tune Regression Model Using Experiment Manager

This example shows how to use Experiment Manager to optimize a machine learning regression model. The goal is to create a regression model for the carbig data set that has minimal cross-validation loss. Begin by using the Regression Learner app to train all available regression models on the training data. Then, improve the best model by exporting it to Experiment Manager.

In Experiment Manager, use the default settings to minimize the cross-validation loss (that is, minimize the cross-validation root mean squared error). Investigate options that help improve the loss, and perform more detailed experiments. For example, fix some hyperparameters at their best values, add useful hyperparameters to the model tuning process, adjust hyperparameter search ranges, adjust the training data, and customize the visualizations. The final result is a model with better test set performance.

For more information on when to export models from Regression Learner to Experiment Manager, see Export Model from Regression Learner to Experiment Manager.

Load and Partition Data

In the MATLAB^® Command Window, load the carbig data set, which contains measurements of cars made in the 1970s and early 1980s.
```
load carbig
```
The goal is to create a regression model that predicts the miles per gallon value for a car, based on the car's other measurements.

Categorize the cars based on whether they were made in the USA.

Origin = categorical(cellstr(Origin));
Origin = mergecats(Origin,["France","Japan","Germany", ...
    "Sweden","Italy","England"],"NotUSA");

Create a table containing the predictor variables Acceleration, Displacement, and so on, as well as the response variable MPG (miles per gallon).
```
cars = table(Acceleration,Displacement,Horsepower, ...
    Model_Year,Origin,Weight,MPG);
```
Remove rows of cars where the table has missing values.
```
cars = rmmissing(cars);
```
Partition the data into two sets. Use approximately 80% of the observations for model training in Regression Learner, and reserve 20% of the observations for a final test set. Use cvpartition to partition the data.
```
rng("default") % For reproducibility
c = cvpartition(height(cars),"Holdout",0.2);
trainingIndices = training(c);
testIndices = test(c);
carsTrain = cars(trainingIndices,:);
carsTest = cars(testIndices,:);
```

Train Models in Regression Learner

If you have Parallel Computing Toolbox™, the Regression Learner app can train models in parallel. Training models in parallel is typically faster than training models in series. If you do not have Parallel Computing Toolbox, skip to the next step.
Before opening the app, start a parallel pool of process workers by using the parpool function.
```
parpool("Processes")
```
By starting a parallel pool of process workers rather than thread workers, you ensure that Experiment Manager can use the same parallel pool later.

Note
Parallel computations with a thread pool are not supported in Experiment Manager.
Open Regression Learner. Click the Apps tab, and then click the arrow at the right of the Apps section to open the apps gallery. In the Machine Learning and Deep Learning group, click Regression Learner.
On the Learn tab, in the File section, click New Session and select From Workspace.
In the New Session from Workspace dialog box, select the carsTrain table from the Data Set Variable list. The app selects the response and predictor variables. The default response variable is MPG.
In the Validation section, specify to use 3-fold cross-validation rather than the default 5-fold cross-validation.
In the Test section, click the check box to set aside a test data set. Specify 25 percent of the imported data as a test set.
To accept the options and continue, click Start Session.
Visually inspect the predictors in the open Response Plot. In the X-axis section, select each predictor from the X list. Note that some of the predictors, such as Displacement, Horsepower, and Weight, display similar trends.
Before training models, use principal component analysis (PCA) to reduce the dimensionality of the predictor space. PCA linearly transforms the numeric predictors to remove redundant dimensions. On the Learn tab, in the Options section, click PCA.
In the Default PCA Options dialog box, click the check box to enable PCA. Select Specify number of components as the component reduction criterion, and specify 4 as the number of numeric components. Click Save and Apply.
To obtain the best model, train all preset models. On the Learn tab, in the Models section, click the arrow to open the gallery. In the Get Started group, click All. In the Train section, click Train All and select Train All. The app trains one of each preset model type, along with the default fine tree model, and displays the models in the Models pane.
To find the best result, sort the trained models based on the validation root mean squared error (RMSE). In the Models pane, open the Sort by list and select RMSE (Validation).
Note
Validation introduces some randomness into the results. Your model validation results can vary from the results shown in this example.

Assess Best Model Performance

For the model with the lowest RMSE, plot the predicted response versus the true response to see how well the regression model makes predictions for different response values. Select the Matern 5/2 GPR model in the Models pane. On the Learn tab, in the Plots and Results section, click the arrow to open the gallery, and then click Predicted vs. Actual (Validation) in the Validation Results group.
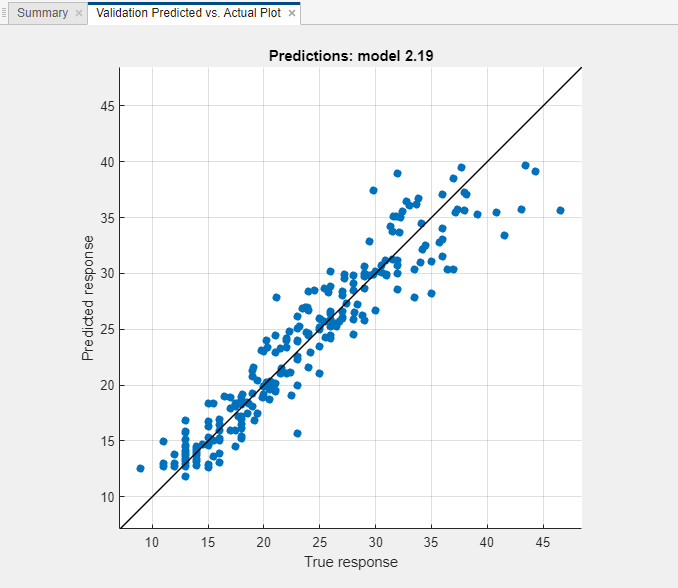
Overall, the GPR (Gaussian process regression) model performs well. Most predictions are near the diagonal line.
View the residuals plot. On the Learn tab, in the Plots and Results section, click the arrow to open the gallery, and then click Residuals (Validation) in the Validation Results group. The residuals plot displays the difference between the true and predicted responses.
The residuals are scattered roughly symmetrically around 0.
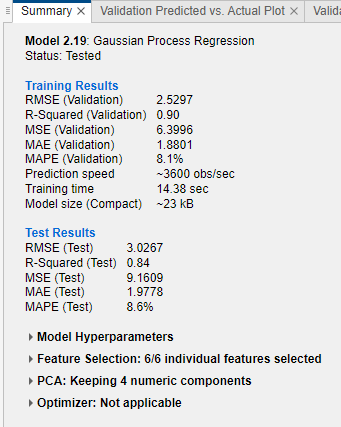
Check the test set performance of the model. On the Test tab, in the Test section, click Test Selected. The app computes the test set performance of the model trained on the full data set, including training and validation data.
Compare the validation and test RMSE for the model. On the model Summary tab, compare the RMSE (Validation) value under Training Results to the RMSE (Test) value under Test Results. In this example, the validation RMSE overestimates the performance of the model on the test set.

Export Model to Experiment Manager

To try to improve the predictive performance of the model, export it to Experiment Manager. On the Learn tab, in the Export section, click Export Model and select Create Experiment. The Create Experiment dialog box opens.
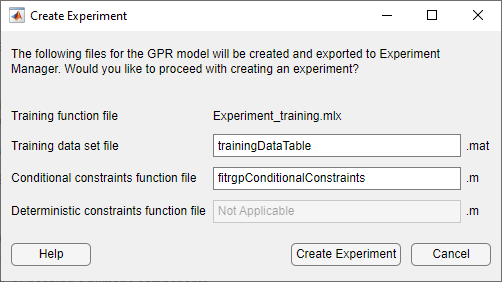
In the Create Experiment dialog box, click Create Experiment. The app opens Experiment Manager and a new dialog box.
In the dialog box, choose a new or existing project for your experiment. For this example, create a new project, and specify TrainGPRModelProject as the filename in the Specify Project Folder Name dialog box.

Run Experiment with Default Hyperparameters

Run the experiment either sequentially or in parallel.
Note
- If you have Parallel Computing Toolbox, save time by running the experiment in parallel. On the Experiment Manager tab, in the Execution section, select Simultaneous from the Mode list.
- Otherwise, use the default Mode option of Sequential.
On the Experiment Manager tab, in the Run section, click Run.
Experiment Manager opens a new tab that displays the results of the experiment. At each trial, the app trains a model with a different combination of hyperparameter values, as specified in the Hyperparameters table in the Experiment1 tab.
After the app runs the experiment, check the results. In the table of results, click the arrow for the ValidationRMSE column and select Sort in Ascending Order.
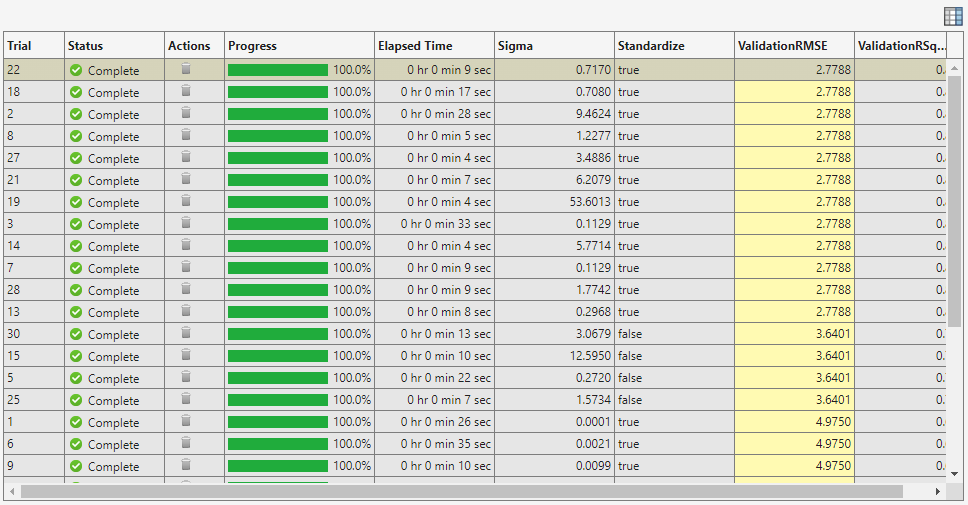
Notice that the app tunes the Sigma and Standardize hyperparameters by default.
Check the predicted vs. actual plot for the model with the lowest RMSE. On the Experiment Manager tab, in the Review Results section, click Predicted vs. Actual (Validation). In the Visualizations pane, the app displays the plot for the model.
To better see the plot, drag the Visualizations pane below the Experiment Browser pane.
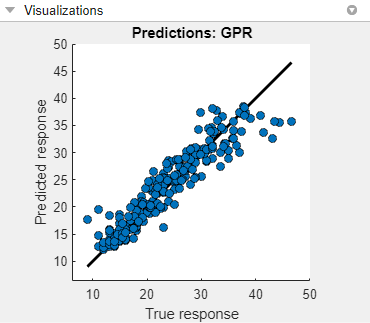
For this model, the predicted values are close to the true response values. However, the model tends to underestimate the true response for values between 40 and 50 miles per gallon.

Adjust Hyperparameters and Hyperparameter Values

Standardizing the numeric predictors before training seems best for this data set. To try to obtain a better model, specify the Standardize hyperparameter value as true and then rerun the experiment. Click the Experiment1 tab. In the Hyperparameters table, select the row for the Standardize hyperparameter. Then click Delete.
Open the training function file. In the Training Function section, click Edit. The app opens the Experiment1_training1.mlx file.

In the file, search for the lines of code that use the fitrgp function. This function is used to create GPR models. Standardize the predictor data by using a name-value argument. In this case, adjust the four calls to fitrgp by adding 'Standardize',true as follows.

regressionGP = fitrgp(predictors, response, ...
    paramNameValuePairs{:}, 'KernelParameters', kernelParameters, ...
    'Standardize', true);

regressionGP = fitrgp(predictors, response, ...
    paramNameValuePairs{:}, 'Standardize', true);

regressionGP = fitrgp(trainingPredictors, trainingResponse, ...
    paramNameValuePairs{:}, 'KernelParameters', kernelParameters, ...
    'Standardize', true);

regressionGP = fitrgp(trainingPredictors, trainingResponse, ...
    paramNameValuePairs{:}, 'Standardize', true);

Save the code changes, and close the file.

On the Experiment Manager tab, in the Run section, click Run.

To further vary the models evaluated during the experiment, add hyperparameters to the model tuning process. In the MATLAB Command Window, use the hyperparameters function to see which hyperparameters you can tune for your model. Specify the training data set to see the default hyperparameter ranges. Enter the following code.

load("trainingDataTable1.mat")
info = hyperparameters("fitrgp",dataTable,"MPG");
for i = 1:length(info)
    disp(i);disp(info(i))
end

     1

  optimizableVariable with properties:

         Name: 'Sigma'
        Range: [1.0000e-04 78.9730]
         Type: 'real'
    Transform: 'log'
     Optimize: 1

     2

  optimizableVariable with properties:

         Name: 'BasisFunction'
        Range: {'constant'  'none'  'linear'  'pureQuadratic'}
         Type: 'categorical'
    Transform: 'none'
     Optimize: 0

     3

  optimizableVariable with properties:

         Name: 'KernelFunction'
        Range: {1×10 cell}
         Type: 'categorical'
    Transform: 'none'
     Optimize: 0

     4

  optimizableVariable with properties:

         Name: 'KernelScale'
        Range: [1.0000e-03 1000]
         Type: 'real'
    Transform: 'log'
     Optimize: 0

     5

  optimizableVariable with properties:

         Name: 'Standardize'
        Range: {'true'  'false'}
         Type: 'categorical'
    Transform: 'none'
     Optimize: 1

Add the BasisFunction, KernelFunction, and KernelScale hyperparameters in Experiment Manager. For each hyperparameter, on the Experiment1 tab, in the Hyperparameters section, click Add. Edit the row entries to match the output of the hyperparameters function.
In particular, specify the BasisFunction range as ["constant","none","linear"] and the KernelFunction range as ["ardexponential","ardmatern32","ardmatern52","ardrationalquadratic","ardsquaredexponential","exponential","matern32","matern52","rationalquadratic","squaredexponential"]. Because the training data set includes a categorical predictor, omit the pureQuadratic value from the list of basis functions.
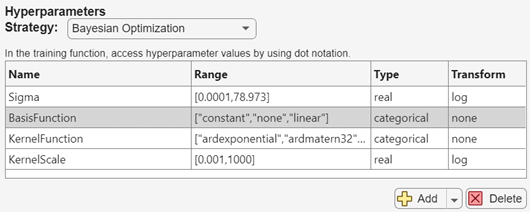
For more information on the hyperparameters you can tune for your model, see Export Model from Regression Learner to Experiment Manager.
For better results when tuning several hyperparameters, increase the number of trials. On the Experiment1 tab, in the Bayesian Optimization Options section, specify 60 as the maximum number of trials.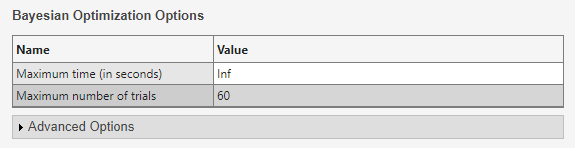
On the Experiment Manager tab, in the Run section, click Run.

Specify Training Data

Before running the experiment again, specify to use all the observations in carsTrain. Because you reserved some observations for testing when you imported the training data into Regression Learner, all experiments so far have used only 75% of the observations in the carsTrain data set.
Save the carsTrain data set as the file fullTrainingData.mat in the TrainGPRModelProject folder, which contains the experiment files. To do so, right-click the carsTrain variable name in the MATLAB workspace, and click Save As. In the dialog box, specify the filename and location, and then click Save.
On the Experiment1 tab, in the Training Function section, click Edit.
In the Experiment1_training1.mlx file, search for the load command. Specify to use the full carsTrain data set for model training by adjusting the code as follows.
```
% Load training data
fileData = load("fullTrainingData.mat");
trainingData = fileData.carsTrain;
```
On the Experiment1 tab, in the Description section, change the number of observations to 314, which is the number of rows in the carsTrain table.
On the Experiment Manager tab, in the Run section, click Run.

Add Residuals Plot

You can add visualizations for Experiment Manager to return at each trial. In this case, specify to create a residuals plot. On the Experiment1 tab, in the Training Function section, click Edit.
In the Experiment1_training1.mlx file, search for the plot function. The surrounding code creates the validation predicted vs. actual plot for each trained model. Enter the following code to create a residuals plot. Ensure that the residuals plot code is within the trainRegressionModel function definition.
```
% Create validation residuals plot
residuals = validationResponse - validationPredictions;
f = figure("Name","Residuals (Validation)");
resAxes = axes(f);
hold(resAxes,"on")
plot(resAxes,validationResponse,residuals,"ko", ...
    "MarkerFaceColor","#D95319")
yline(resAxes,0)
xlabel(resAxes,"True response")
ylabel(resAxes,"Residuals (MPG)")
title(resAxes,"Predictions: GPR")
```
On the Experiment Manager tab, in the Run section, click Run.
In the table of results, click the arrow for the ValidationRMSE column and select Sort in Ascending Order.
Check the predicted vs. actual plot and the residuals plot for the model with the lowest RMSE. On the Experiment Manager tab, in the Review Results section, click Predicted vs. Actual (Validation). In the Visualizations pane, the app displays the plot for the model.
On the Experiment Manager tab, in the Review Results section, click Residuals (Validation). In the Visualizations pane, the app displays the plot for the model.
Both plots indicate that the model generally performs well.

Export and Use Final Model

You can export a model trained in Experiment Manager to the MATLAB workspace. Select the best-performing model from the most recently run experiment. On the Experiment Manager tab, in the Export section, click Export and select Training Output.
In the Export dialog box, change the workspace variable name to finalGPRModel and click OK.
The new variable appears in your workspace.
Use the exported finalGPRModel structure to make predictions using new data. You can use the structure in the same way that you use any trained model exported from the Regression Learner app. For more information, see Make Predictions for New Data Using Exported Model.
In this case, predict the response values for the test data in carsTest.
```
testPredictedY = finalGPRModel.predictFcn(carsTest);
```
Compute the test RMSE using the predicted response values.
```
testRSME = sqrt((1/length(testPredictedY))* ...
    sum((carsTest.MPG - testPredictedY).^2))
```
```
testRSME =

    2.6647
```
The test RMSE is close to the validation RMSE computed in Experiment Manager (2.6894). Also, the test RMSE for this tuned model is smaller than the test RMSE for the Matern 5/2 GPR model in Regression Learner (3.0267). However, keep in mind that the tuned model uses observations in carsTest as test data and the Regression Learner model uses a subset of the observations in carsTrain as test data.

Create a predicted vs. actual plot and a residuals plot using the true test data response and the predicted response.

figure
line([min(carsTest.MPG) max(carsTest.MPG)], ...
    [min(carsTest.MPG) max(carsTest.MPG)], ...,
    "Color","black","LineWidth",2);
hold on
plot(carsTest.MPG,testPredictedY,"ko", ...
    "MarkerFaceColor","#0072BD");
hold off
xlabel("True response")
ylabel("Predicted response")

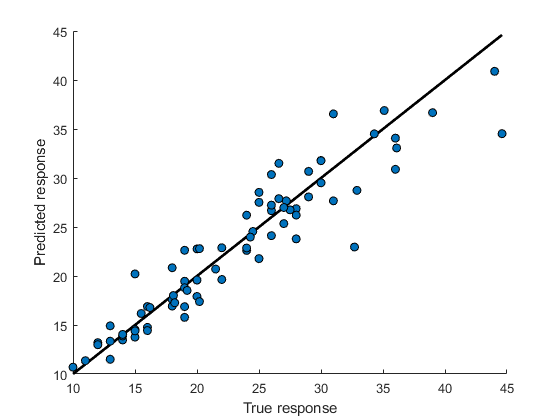
Test Predicted vs. Actual plot for the exported GPR model

figure
residuals = carsTest.MPG - testPredictedY;
plot(carsTest.MPG,residuals,"ko", ...
    "MarkerFaceColor","#D95319")
hold on
yline(0)
hold off
xlabel("True response")
ylabel("Residuals (MPG)")

Test residuals plot for the exported GPR model

Both plots indicate that the model performs well on the test set.