Regularize Logistic Regression
This example shows how to regularize binomial regression. The default (canonical) link function for binomial regression is the logistic function.
Step 1. Prepare the data.
Load the ionosphere data. The response Y is a cell array of 'g' or 'b' characters. Convert the cells to logical values, with true representing 'g'. Remove the first two columns of X because they have some awkward statistical properties, which are beyond the scope of this discussion.
load ionosphere Ybool = strcmp(Y,'g'); X = X(:,3:end);
Step 2. Create a cross-validated fit.
Construct a regularized binomial regression using 25 Lambda values and 10-fold cross validation. This process can take a few minutes.
rng('default') % for reproducibility [B,FitInfo] = lassoglm(X,Ybool,'binomial',... 'NumLambda',25,'CV',10);
Step 3. Examine plots to find appropriate regularization.
lassoPlot can give both a standard trace plot and a cross-validated deviance plot. Examine both plots.
lassoPlot(B,FitInfo,'PlotType','CV'); legend('Location','best') % show legend
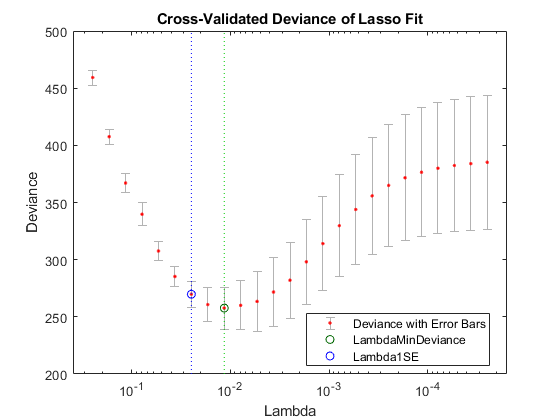
The plot identifies the minimum-deviance point with a green circle and dashed line as a function of the regularization parameter Lambda. The blue circled point has minimum deviance plus no more than one standard deviation.
lassoPlot(B,FitInfo,'PlotType','Lambda','XScale','log');
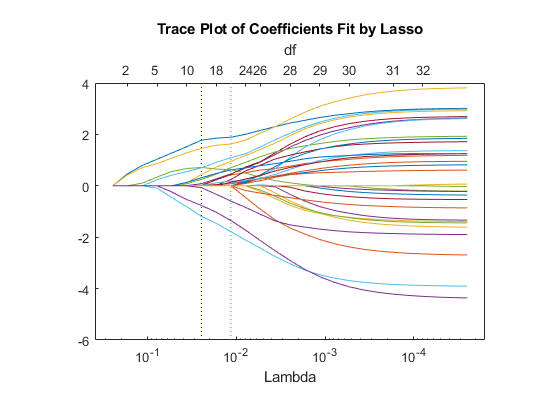
The trace plot shows nonzero model coefficients as a function of the regularization parameter Lambda. Because there are 32 predictors and a linear model, there are 32 curves. As Lambda increases to the left, lassoglm sets various coefficients to zero, removing them from the model.
The trace plot is somewhat compressed. Zoom in to see more detail.
xlim([.01 .1]) ylim([-3 3])
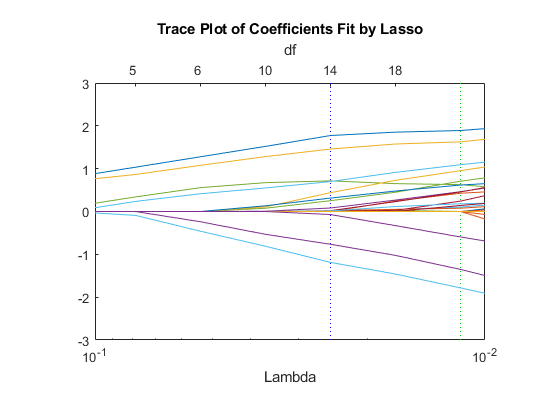
As Lambda increases toward the left side of the plot, fewer nonzero coefficients remain.
Find the number of nonzero model coefficients at the Lambda value with minimum deviance plus one standard deviation point. The regularized model coefficients are in column FitInfo.Index1SE of the B matrix.
indx = FitInfo.Index1SE; B0 = B(:,indx); nonzeros = sum(B0 ~= 0)
nonzeros = 14
When you set Lambda to FitInfo.Index1SE, lassoglm removes over half of the 32 original predictors.
Step 4. Create a regularized model.
The constant term is in the FitInfo.Index1SE entry of the FitInfo.Intercept vector. Call that value cnst.
The model is logit(mu) = log(mu/(1 - mu)) = X*B0 + cnst. Therefore, for predictions, mu = exp(X*B0 + cnst)/(1+exp(x*B0 + cnst)).
The glmval function evaluates model predictions. It assumes that the first model coefficient relates to the constant term. Therefore, create a coefficient vector with the constant term first.
cnst = FitInfo.Intercept(indx); B1 = [cnst;B0];
Step 5. Examine residuals.
Plot the training data against the model predictions for the regularized lassoglm model.
preds = glmval(B1,X,'logit'); histogram(Ybool - preds) % plot residuals title('Residuals from lassoglm model')
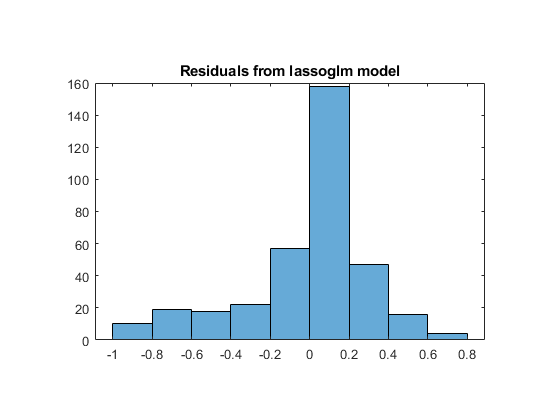
Step 6. Alternative: Use identified predictors in a least-squares generalized linear model.
Instead of using the biased predictions from the model, you can make an unbiased model using just the identified predictors.
predictors = find(B0); % indices of nonzero predictors mdl = fitglm(X,Ybool,'linear',... 'Distribution','binomial','PredictorVars',predictors)
mdl =
Generalized linear regression model:
logit(y) ~ 1 + x1 + x3 + x4 + x5 + x6 + x7 + x12 + x16 + x20 + x24 + x25 + x27 + x29 + x32
Distribution = Binomial
Estimated Coefficients:
Estimate SE tStat pValue
_________ _______ ________ __________
(Intercept) -2.9367 0.50926 -5.7666 8.0893e-09
x1 2.492 0.60795 4.099 4.1502e-05
x3 2.5501 0.63304 4.0284 5.616e-05
x4 0.48816 0.50336 0.9698 0.33215
x5 0.6158 0.62192 0.99015 0.3221
x6 2.294 0.5421 4.2317 2.3198e-05
x7 0.77842 0.57765 1.3476 0.1778
x12 1.7808 0.54316 3.2786 0.0010432
x16 -0.070993 0.50515 -0.14054 0.88823
x20 -2.7767 0.55131 -5.0365 4.7402e-07
x24 2.0212 0.57639 3.5067 0.00045372
x25 -2.3796 0.58274 -4.0835 4.4363e-05
x27 0.79564 0.55904 1.4232 0.15467
x29 1.2689 0.55468 2.2876 0.022162
x32 -1.5681 0.54336 -2.8859 0.0039035
351 observations, 336 error degrees of freedom
Dispersion: 1
Chi^2-statistic vs. constant model: 262, p-value = 1e-47
Plot the residuals of the model.
plotResiduals(mdl)
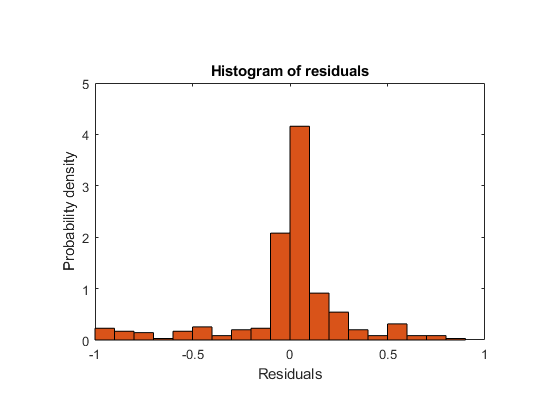
As expected, residuals from the least-squares model are slightly smaller than those of the regularized model. However, this does not mean that mdl is a better predictor for new data.