Linear Regression with Categorical Covariates
This example shows how to perform a regression with categorical
covariates using categorical arrays and fitlm.
Load sample data.
load carsmallThe variable MPG contains measurements on the miles per
gallon of 100 sample cars. The model year of each car is in the variable
Model_Year, and Weight contains the
weight of each car.
Plot grouped data.
Draw a scatter plot of MPG against
Weight, grouped by model year.
figure() gscatter(Weight,MPG,Model_Year,'bgr','x.o') title('MPG vs. Weight, Grouped by Model Year')
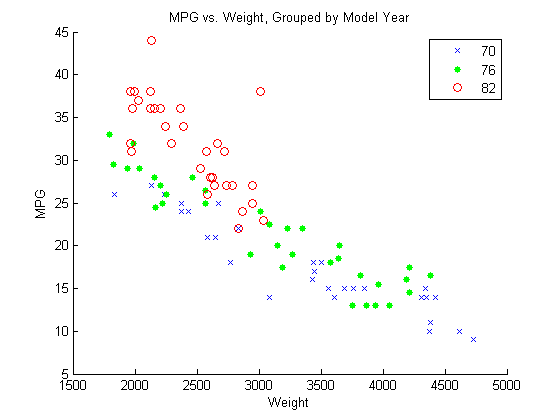
The grouping variable, Model_Year, has three
unique values, 70, 76, and
82, corresponding to model years 1970, 1976, and
1982.
Create table and categorical array.
Create a table that contains the variables MPG,
Weight, and Model_Year. Convert the
variable Model_Year to a categorical array.
cars = table(MPG,Weight,Model_Year); cars.Model_Year = categorical(cars.Model_Year);
Fit a regression model.
Fit a regression model using fitlm with
MPG as the dependent variable, and
Weight and Model_Year as the
independent variables. Because Model_Year is a categorical
covariate with three levels, it should enter the model as two indicator
variables.
The scatter plot suggests that the slope of MPG against
Weight might differ for each model year. To assess this,
include weight-year interaction terms.
The proposed model is
where I[1976] and I[1982] are dummy variables indicating the model years 1976 and 1982, respectively. I[1976] takes the value 1 if model year is 1976 and takes the value 0 if it is not. I[1982] takes the value 1 if model year is 1982 and takes the value 0 if it is not. In this model, 1970 is the reference year.
fit = fitlm(cars,'MPG~Weight*Model_Year')fit =
Linear regression model:
MPG ~ 1 + Weight*Model_Year
Estimated Coefficients:
Estimate SE
___________ __________
(Intercept) 37.399 2.1466
Weight -0.0058437 0.00061765
Model_Year_76 4.6903 2.8538
Model_Year_82 21.051 4.157
Weight:Model_Year_76 -0.00082009 0.00085468
Weight:Model_Year_82 -0.0050551 0.0015636
tStat pValue
________ __________
(Intercept) 17.423 2.8607e-30
Weight -9.4612 4.6077e-15
Model_Year_76 1.6435 0.10384
Model_Year_82 5.0641 2.2364e-06
Weight:Model_Year_76 -0.95953 0.33992
Weight:Model_Year_82 -3.2329 0.0017256
Number of observations: 94, Error degrees of freedom: 88
Root Mean Squared Error: 2.79
R-squared: 0.886, Adjusted R-Squared: 0.88
F-statistic vs. constant model: 137, p-value = 5.79e-40The regression output shows:
fitlmrecognizesModel_Yearas a categorical variable, and constructs the required indicator (dummy) variables. By default, the first level,70, is the reference group (usereordercatsto change the reference group).The model specification,
MPG~Weight*Model_Year, specifies the first-order terms forWeightandModel_Year, and all interactions.The model R2 = 0.886, meaning the variation in miles per gallon is reduced by 88.6% when you consider weight, model year, and their interactions.
The fitted model is
Thus, the estimated regression equations for the model years are as follows.
Model Year Predicted MPG Against Weight 1970 1976 1982
The relationship between MPG and Weight
has an increasingly negative slope as the model year increases.
Plot fitted regression lines.
Plot the data and fitted regression lines.
w = linspace(min(Weight),max(Weight)); figure() gscatter(Weight,MPG,Model_Year,'bgr','x.o') line(w,feval(fit,w,'70'),'Color','b','LineWidth',2) line(w,feval(fit,w,'76'),'Color','g','LineWidth',2) line(w,feval(fit,w,'82'),'Color','r','LineWidth',2) title('Fitted Regression Lines by Model Year')

Test for different slopes.
Test for significant differences between the slopes. This is equivalent to testing the hypothesis
anova(fit)
ans =
SumSq DF MeanSq F pValue
Weight 2050.2 1 2050.2 263.87 3.2055e-28
Model_Year 807.69 2 403.84 51.976 1.2494e-15
Weight:Model_Year 81.219 2 40.609 5.2266 0.0071637
Error 683.74 88 7.7698 0.0072 (from the interaction row,
Weight:Model_Year), so the null hypothesis is rejected at
the 0.05 significance level. The value of the test statistic is
5.2266. The numerator degrees of freedom for the test is
2, which is the number of coefficients in the null
hypothesis.There is sufficient evidence that the slopes are not equal for all three model years.
See Also
fitlm | categorical | reordercats | anova