Noncentral F Distribution
Definition
Similar to the noncentral χ2 distribution, the toolbox calculates noncentral F distribution probabilities as a weighted sum of incomplete beta functions using Poisson probabilities as the weights.
I(x|a,b) is the incomplete beta function with parameters a and b, and δ is the noncentrality parameter.
Background
As with the χ2 distribution, the F distribution is a special case of the noncentral F distribution. The F distribution is the result of taking the ratio of χ2 random variables each divided by its degrees of freedom.
If the numerator of the ratio is a noncentral chi-square random variable divided by its degrees of freedom, the resulting distribution is the noncentral F distribution.
The main application of the noncentral F distribution is to calculate the power of a hypothesis test relative to a particular alternative.
Examples
Compute Noncentral F Distribution pdf
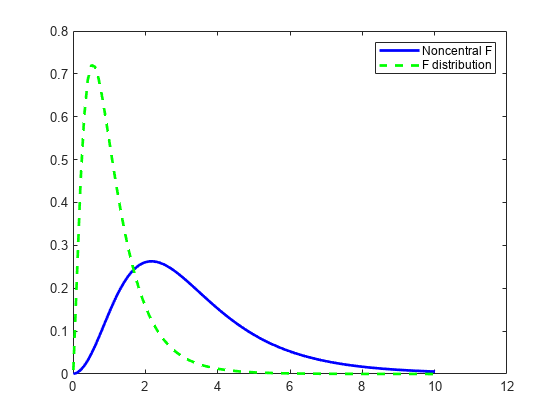
Compute the pdf of a noncentral F distribution with degrees of freedom NU1 = 5 and NU2 = 20, and noncentrality parameter DELTA = 10. For comparison, also compute the pdf of an F distribution with the same degrees of freedom.
x = (0.01:0.1:10.01)'; p1 = ncfpdf(x,5,20,10); p = fpdf(x,5,20);
Plot the pdf of the noncentral F distribution and the pdf of the F distribution on the same figure.
figure; plot(x,p1,'b-','LineWidth',2) hold on plot(x,p,'g--','LineWidth',2) legend('Noncentral F','F distribution')
See Also
ncfcdf | ncfpdf | ncfinv | ncfstat | ncfrnd | random