Half-Normal Distribution
Overview
The half-normal distribution is a special case of the folded normal and truncated normal distributions. Some applications of the half-normal distribution include modeling measurement data and lifetime data.
Parameters
The half-normal distribution uses the following parameters:
| Parameter | Description |
|---|---|
| Location parameter | |
| Scale parameter |
The support for the half-normal distribution is x ≥ μ.
Use makedist with specified parameter
values to create a half-normal probability distribution object HalfNormalDistribution. Use fitdist to fit a half-normal probability distribution object to
sample data. Use mle to estimate the half-normal
distribution parameter values from sample data without creating a probability
distribution object. For more information about working with probability
distributions, see Working with Probability Distributions.
The Statistics and Machine Learning Toolbox™ implementation of the half-normal distribution assumes a fixed value
for the location parameter μ. Therefore, neither
fitdist nor mle estimates the value of
the parameter μ when fitting a half-normal distribution to sample
data. You can specify a value for the μ parameter by using the
name-value pair argument 'mu'. The default value for the
'mu' argument is 0 in both fitdist and
mle.
Probability Density Function
The probability density function (pdf) of the half-normal distribution is
where μ is the location parameter and σ is the scale parameter. If x ≤ μ, then the pdf is undefined.
To compute the pdf of the half-normal distribution, create a HalfNormalDistribution probability distribution object using fitdist or makedist, then use the pdf method to work with the object.
pdf of Half-Normal Probability Distribution
This example shows how changing the values of the mu and sigma parameters alters the shape of the pdf.
Create four probability distribution objects with different parameters.
pd1 = makedist('HalfNormal'); pd2 = makedist('HalfNormal','mu',0,'sigma',2); pd3 = makedist('HalfNormal','mu',0,'sigma',3); pd4 = makedist('HalfNormal','mu',0,'sigma',5);
Compute the probability density functions (pdfs) of each distribution.
x = 0:0.1:10; pdf1 = pdf(pd1,x); pdf2 = pdf(pd2,x); pdf3 = pdf(pd3,x); pdf4 = pdf(pd4,x);
Plot the pdfs on the same figure.
figure; plot(x,pdf1,'r','LineWidth',2) hold on; plot(x,pdf2,'k:','LineWidth',2); plot(x,pdf3,'b-.','LineWidth',2); plot(x,pdf4,'g--','LineWidth',2); legend({'mu = 0, sigma = 1','mu = 0, sigma = 2',... 'mu = 0, sigma = 3','mu = 0, sigma = 5'},'Location','NE'); hold off;

As sigma increases, the curve flattens and the peak value becomes smaller.
Cumulative Distribution Function
The cumulative distribution function (cdf) of the half-normal distribution is
where μ is the location parameter, σ is the scale parameter, erf(•) is the error function, and Φ(•) is the cdf of the standard normal distribution. If x ≤ μ, then the cdf is undefined.
To compute the cdf of the half-normal distribution, create a HalfNormalDistribution probability distribution object using fitdist or makedist, then use the cdf method to work with the object.
CDF of Half-Normal Probability Distribution
This example shows how changing the values of the mu and sigma parameters alters the shape of the cdf.
Create four probability distribution objects with different parameters.
pd1 = makedist('HalfNormal'); pd2 = makedist('HalfNormal','mu',0,'sigma',2); pd3 = makedist('HalfNormal','mu',0,'sigma',3); pd4 = makedist('HalfNormal','mu',0,'sigma',5);
Compute the cumulative distribution functions (cdfs) for each probability distribution.
x = 0:0.1:10; cdf1 = cdf(pd1,x); cdf2 = cdf(pd2,x); cdf3 = cdf(pd3,x); cdf4 = cdf(pd4,x);
Plot all four cdfs on the same figure.
figure; plot(x,cdf1,'r','LineWidth',2) hold on; plot(x,cdf2,'k:','LineWidth',2); plot(x,cdf3,'b-.','LineWidth',2); plot(x,cdf4,'g--','LineWidth',2); legend({'mu = 0, sigma = 1','mu = 0, sigma = 2',... 'mu = 0, sigma = 3','mu = 0, sigma = 5'},'Location','SE'); hold off;
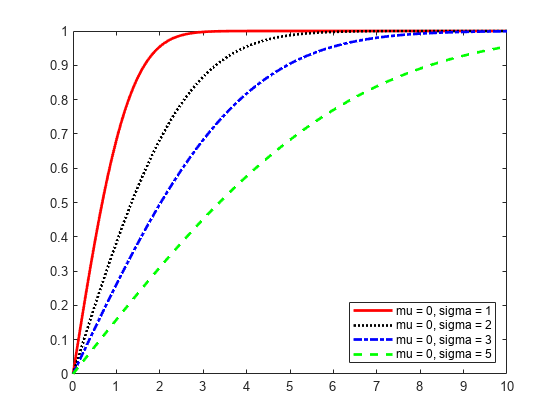
As sigma increases, the curve of the cdf flattens.
Descriptive Statistics
The mean of the half-normal distribution is
where μ is the location parameter and σ is the scale parameter.
The variance of the half-normal distribution is
where σ is the scale parameter.
Relationship to Other Distributions
If a random variable Z has a standard normal distribution with
a mean μ equal to zero and standard deviation
σ equal to one, then has a half-normal distribution with parameters
μ and σ.
References
[1] Cooray, K. and M.M.A. Ananda. “A Generalization of the Half-Normal Distribution with Applications to Lifetime Data.” Communications in Statistics – Theory and Methods. Vol. 37, Number 9, 2008, pp. 1323–1337.
[2] Pewsey, A. “Large-Sample Inference for the General Half-Normal Distribution.” Communications in Statistics – Theory and Methods. Vol. 31, Number 7, 2002, pp. 1045–1054.