Transmission Line
Delay-based or lumped parameter transmission line
Libraries:
Simscape /
Electrical /
Passive /
Lines
Description
The Transmission Line block lets you choose between the following models of a transmission line:
Delay-based and lossless
Delay-based and lossy
Lumped parameter L-section
Lumped parameter pi-section
Distributed parameter line
The first option provides the best simulation performance, with options 2, 3 and 4 requiring progressively more computing power.
Delay-Based and Lossless
This first option, Delay-based and lossless, models the
transmission line as a fixed impedance, irrespective of frequency, plus a delay
term. The defining equations are:
| v1( t ) – i1( t ) Z0 = v2( t – τ ) + i( t – τ ) Z0 | (1) |
2
| v2( t ) – i2( t ) Z0 = v1( t – τ ) + i1( t – τ ) Z0 | (2) |
where:
v1 is the voltage across the left-hand end of the transmission line.
i1 is the current into the left-hand end of the transmission line.
v2 is the voltage across the right-hand end of the transmission line.
i2 is the current into the right-hand end of the transmission line.
τ is the transmission line delay.
Z0 is the line characteristic impedance.
Delay-Based and Lossy
To introduce losses, the second option, Delay-based and
lossy, connects N delay-based components, each
defined by the above equations, in series via a set of resistors, as shown in the
following illustration.

N is an integer greater than or equal to 1. r = R · LEN / N, where R is the line resistance per unit length and LEN is the line length.
Lumped Parameter L-Section
The following block diagram shows the model of one L-line segment.

The lumped parameter parameterization uses N copies of the above segment model connected in series.
Parameters are as follows:
R is line resistance per unit length.
L is the line inductance per unit length.
C is the line capacitance per unit length.
G is the line conductance per unit length.
LEN is the length of the line.
N is the number of series segments.
Lumped Parameter Pi-Section
The following block diagram shows the model of one pi-line segment.

The lumped parameter parameterization uses N copies of the above segment model connected in series. The parameters are as defined for the L-section transmission line model. Unlike the L-section model, the pi-section model is symmetric.
Lumped Parameter Line Model Parameterization
The lumped-parameter models (L-section or pi-section) are the most challenging to simulate, typically needing many more segments (greater N) than for the delay-based and lossy model [1].
Cable manufacturers do not typically quote an inductance value per unit length, but instead give the characteristic impedance. The inductance, capacitance, and characteristic impedance are related by:
| L = C · Z02 | (3) |
The block lets you specify either L or Z0 when using the lumped parameter model.
Distributed parameter line
A distributed parameter line gives more accurate simulation at particular frequency compared to the other options provided by this block. However, this is not a frequency-dependent model. The accuracy of the model will drop outside the frequency point specified in the Frequency used for rlcg specification parameter.
For a frequency-dependent transmission line model, see Frequency-Dependent Overhead Line (Three-Phase).
The electromagnetic behavior of a multiconductor transmission line is described by the telegrapher's equation.
| (4) |
| (5) |
Define:
— Shunt current vector produced at terminal 1 by injected voltages V1
— Shunt current vector produced at terminal 2 by injected voltages V2
— Reflected currents of terminal 1
— Reflected currents of terminal 2
You can then rewrite and solve equations 4 and 5:
The following block diagram shows the equivalent circuit for a distributed parameter line.
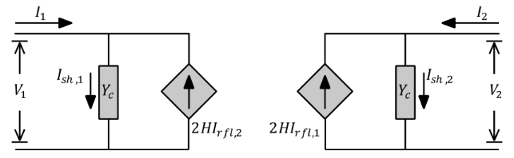
Assumptions and Limitations
For the lumped parameter options, MathWorks recommends that you use a trapezoidal solver such as
ode23t. This is because lumped parameter transmission models have very lightly damped internal dynamics, which are best suited to trapezoidal solvers for numerical accuracy.The lumped parameter pi-section model has a parallel capacitor at both ends. This means that you should not connect it directly to an ideal voltage source, that is, a source with no internal resistance. The lumped parameter L-section model, however, has a series input resistor, and therefore you can connect it directly to an ideal voltage source.
Ports
Refer to the figure for port locations.

Conserving
Parameters
References
[1] Sussman-Fort, S.E. and J.C. Hantgan. “SPICE Implementation of Lossy Transmission Line and Schottky Diode Models.” IEEE Transactions on Microwave Theory and Techniques. Vol. 36, No. 1, January, 1988.
Extended Capabilities
Version History
Introduced in R2012a


