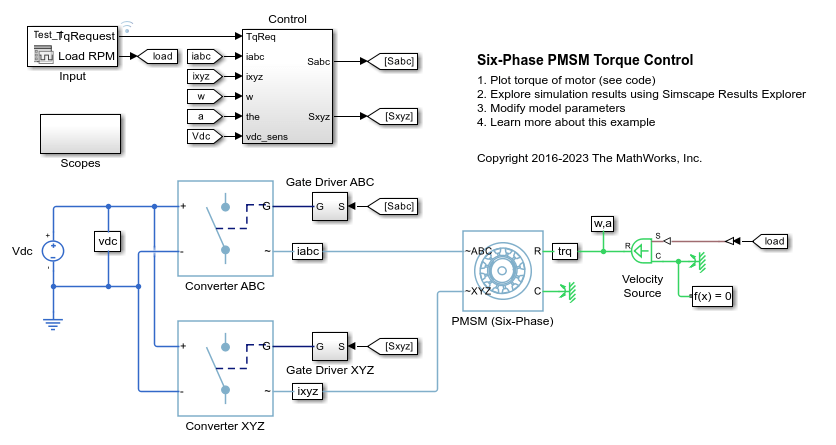
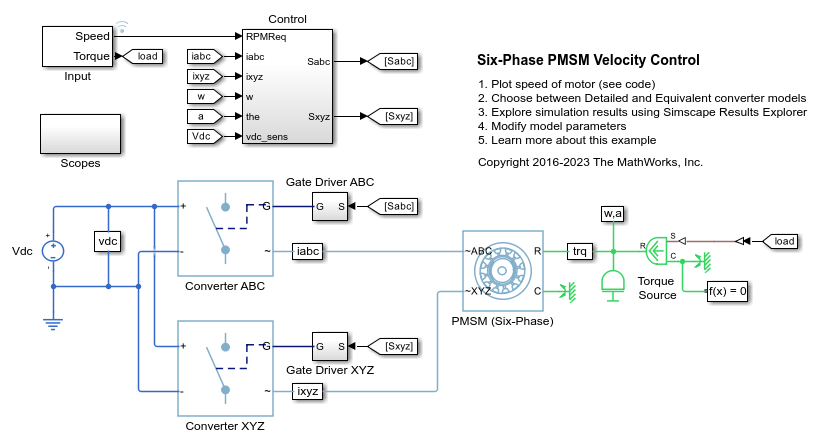
PMSM (Six-Phase)

Six-phase permanent magnet synchronous motor with sinusoidal flux distribution

Since R2020b

• 

Libraries:
Simscape / Electrical / Electromechanical / Permanent Magnet

Description

The PMSM (Six-Phase) block models a permanent magnet synchronous machine (PMSM) with a six-phase star-wound stator. Use this block to model these types of motor if the motor has six stator windings: an interior permanent magnet synchronous machine (IPMSM), surface permanent magnet synchronous machine (SPMSM), axial flux (pancake) motor, or PMSM servomotor.

A six-phase PMSM has two groups of three-phase stator windings: the ABC group and the XYZ group. These two groups have a 30 degree phase shift.

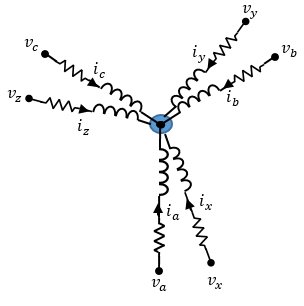
The figure shows the equivalent electrical circuit for the stator windings.

Equations

The voltages across the stator windings are

$$\left[\begin{array}{l}{v}_a\\ v_b\\ v_c\\ v_x\\ v_y\\ v_z\end{array}\right]=\left[\begin{array}{cccccc}{R}_s& 0& 0& 0& 0& 0\\ 0& R_s& 0& 0& 0& 0\\ 0& 0& R_s& 0& 0& 0\\ 0& 0& 0& R_s& 0& 0\\ 0& 0& 0& 0& R_s& 0\\ 0& 0& 0& 0& 0& R_s\end{array}\right]\left[\begin{array}{l}{i}_a\\ i_b\\ i_c\\ i_x\\ i_y\\ i_z\end{array}\right]+\left[\begin{array}{l}\frac{d{\psi }_a}{dt}\\ \frac{d{\psi }_b}{dt}\\ \frac{d{\psi }_c}{dt}\\ \frac{d{\psi }_x}{dt}\\ \frac{d{\psi }_y}{dt}\\ \frac{d{\psi }_z}{dt}\end{array}\right],$$

where:

• v_a, v_b, and v_c are the individual phase voltages from port ~ABC to neutral port n1.

• v_x, v_y, and v_z are the individual phase voltages from port ~XYZ to neutral port n2.

• R_s is the equivalent resistance of each stator winding.

• i_a, i_b, and i_c are the currents flowing from port ~ABC to port n1.

• i_x, i_y, and i_z are the currents flowing from port ~XYZ to port n2.

• $$\frac{d{\psi }_a}{dt},$$$$\frac{d{\psi }_b}{dt},$$$$\frac{d{\psi }_c}{dt}$$ $$\frac{d{\psi }_x}{dt},$$ $$\frac{d{\psi }_y}{dt},$$ and $$\frac{d{\psi }_z}{dt}$$ are the rates of change for the magnetic flux in each stator winding.

The permanent magnet and the six windings contribute to the total flux linking each winding. The total flux is

$$\left[\begin{array}{l}{\psi }_a\\ {\psi }_b\\ {\psi }_c\\ {\psi }_x\\ {\psi }_y\\ {\psi }_z\end{array}\right]=\left[\begin{array}{cccccc}{L}_{aa}& L_{ab}& L_{ac}& L_{ax}& L_{ay}& L_{az}\\ L_{ba}& L_{bb}& L_{bc}& L_{bx}& L_{by}& L_{bz}\\ L_{ca}& L_{cb}& L_{cc}& L_{cx}& L_{cy}& L_{cz}\\ L_{xa}& L_{xb}& L_{xc}& L_{xx}& L_{xy}& L_{xz}\\ L_{ya}& L_{yb}& L_{yc}& L_{yx}& L_{yy}& L_{yz}\\ L_{za}& L_{zb}& L_{zc}& L_{zx}& L_{zy}& L_{zz}\end{array}\right]\left[\begin{array}{l}{i}_a\\ i_b\\ i_c\\ i_x\\ i_y\\ i_z\end{array}\right]+\left[\begin{array}{l}{\psi }_{am}\\ {\psi }_{bm}\\ {\psi }_{cm}\\ {\psi }_{xm}\\ {\psi }_{ym}\\ {\psi }_{zm}\end{array}\right],$$

where:

• ψ_a, ψ_b, ψ_c, ψ_x, ψ_y, and ψ_z are the total fluxes that link each stator winding.

• L_aa, L_bb, L_cc, L_xx, L_yy, and L_zz are the self-inductances of the stator windings. These self-inductances are a function of the rotor electrical angle, θ_e, and depend on the stator per-phase self-inductance, L_s, and the stator inductance fluctuation, L_m.

  • ${\theta }_e=N{\theta }_r+rotoroffset$ where θ_r is the rotor mechanical angle.

  • rotor offset is 0 if you define the rotor electrical angle with respect to the d-axis, or -pi/2 if you define the rotor electrical angle with respect to the q-axis.

  • L_s is the stator per-phase self-inductance. This value is the average self-inductance of each of the stator windings.

  • L_m is the stator inductance fluctuation. This value is the amount the self-inductance and mutual inductance fluctuate with the changing of the rotor angle.

• L_ab, L_ac, L_ba, and so on, are the mutual inductances of the stator windings. These mutual inductances are a function of the rotor electrical angle, θ_e, and depend on the stator mutual inductance, M_s, and the stator per-phase self-inductance, L_s.

  • M_s is the stator mutual inductance. This value is the average mutual inductance between the stator windings.

• ψ_am, ψ_bm, ψ_cm, ψ_xm, ψ_ym, and ψ_zm are the permanent magnet fluxes linking the stator windings.

The permanent magnet flux linking winding a-a' is at maximum when θ_e = 0° and zero when θ_e = 90°. Therefore, the linked motor flux is defined by:

$$\left[\begin{array}{l}{\psi }_{am}\\ {\psi }_{bm}\\ {\psi }_{cm}\\ {\psi }_{xm}\\ {\psi }_{ym}\\ {\psi }_{zm}\end{array}\right]=\left[\begin{array}{l}{\psi }_m\cos {\theta }_e\\ {\psi }_m\cos ({\theta }_e-2\pi /3)\\ {\psi }_m\cos ({\theta }_e+2\pi /3)\\ {\psi }_m\cos ({\theta }_e-\pi /6)\\ {\psi }_m\cos ({\theta }_e-5\pi /6)\\ {\psi }_{m}cos({\theta }_e+\pi /2)\end{array}\right],$$

where ψ_m is the permanent magnet flux linkage.

Simplified Electrical Equations

Applying a decoupled transformation to the block electrical equations produces an expression for torque that is independent of the rotor angle.

The decoupled transformation is defined by:

$$P({\theta }_e)=\frac{1}{3}\left[\begin{array}{cccccc}\cos {\theta }_e& \cos \left({\theta }_e-2\frac{\pi }{3}\right)& \cos \left({\theta }_e+2\frac{\pi }{3}\right)& cos\left({\theta }_e-\frac{\pi }{6}\right)& \cos \left({\theta }_e-5\frac{\pi }{6}\right)& \cos \left({\theta }_e+\frac{\pi }{2}\right)\\ -\sin {\theta }_e& -\sin \left({\theta }_e-2\frac{\pi }{3}\right)& -\sin \left({\theta }_e+2\frac{\pi }{3}\right)& -\sin \left({\theta }_e-\frac{\pi }{6}\right)& -\sin \left({\theta }_e-5\frac{\pi }{6}\right)& -\sin \left({\theta }_e+\frac{\pi }{2}\right)\\ 1& -\frac{1}{2}& -\frac{1}{2}& -\frac{\sqrt{3}}{2}& \frac{\sqrt{3}}{2}& 0\\ 0& -\frac{\sqrt{3}}{2}& \frac{\sqrt{3}}{2}& \frac{1}{2}& \frac{1}{2}& -1\\ 1& 1& 1& 0& 0& 0\\ 0& 0& 0& 1& 1& 1\end{array}\right].$$

The transformation matrix, P, has this pseudo-orthogonal property:

$$P^{-1}({\theta }_e)=3P^T({\theta }_e).$$

Using the decoupled transformation on the stator winding voltages and currents transforms them to the dq0 frame, which is independent of the rotor angle.

To obtain the d-axis, q-axis, and zero-sequence stator voltages and flux linkages for the ABC and XYZ groups, apply the transformation to the voltage and flux linkage equations:

$$\left[\begin{array}{l}{v}_d\\ v_q\\ v_{z1}\\ v_{z2}\\ v_{01}\\ v_{02}\end{array}\right]=\left[\begin{array}{cccccc}{R}_s& 0& 0& 0& 0& 0\\ 0& R_s& 0& 0& 0& 0\\ 0& 0& R_s& 0& 0& 0\\ 0& 0& 0& R_s& 0& 0\\ 0& 0& 0& 0& R_s& 0\\ 0& 0& 0& 0& 0& R_s\end{array}\right]\left[\begin{array}{l}{i}_d\\ i_q\\ i_{z1}\\ i_{z2}\\ i_{01}\\ i_{02}\end{array}\right]+\left[\begin{array}{c}-{\psi }_q\\ {\psi }_d\\ 0\\ 0\\ 0\\ 0\end{array}\right]N\omega +\frac{d}{dt}\left[\begin{array}{c}{\psi }_d\\ {\psi }_q\\ {\psi }_{z1}\\ {\psi }_{z2}\\ {\psi }_{01}\\ {\psi }_{02}\end{array}\right]$$

$$\left[\begin{array}{c}{\psi }_d\\ {\psi }_q\\ {\psi }_{z1}\\ {\psi }_{z2}\\ {\psi }_{01}\\ {\psi }_{02}\end{array}\right]=\left[\begin{array}{cccccc}{L}_d& 0& 0& 0& 0& 0\\ 0& L_q& 0& 0& 0& 0\\ 0& 0& L_0& 0& 0& 0\\ 0& 0& 0& L_0& 0& 0\\ 0& 0& 0& 0& L_0& 0\\ 0& 0& 0& 0& 0& L_0\end{array}\right]\left[\begin{array}{l}{i}_d\\ i_q\\ i_{z1}\\ i_{z2}\\ i_{01}\\ i_{02}\end{array}\right]+\left[\begin{array}{c}{\psi }_m\\ 0\\ 0\\ 0\\ 0\\ 0\end{array}\right]$$

where:

• v_d, v_q, v_z1, v_z2, v₀₁, and v₀₂ are the d, q, z1, and z2 components and zero-sequence stator voltages for the ABC and XYZ groups, defined by:

  $$\left[\begin{array}{l}{v}_d\\ v_q\\ v_{z1}\\ v_{z2}\\ v_{01}\\ v_{02}\end{array}\right]=P\left[\begin{array}{l}{v}_a\\ v_b\\ v_c\\ v_x\\ v_y\\ v_z\end{array}\right].$$

• i_d, i_q, i_z1, i_z2, i₀₁, and i₀₂ are the d-axis, q-axis, and zero-sequence stator currents for the ABC and XYZ groups, defined by:

  $$\left[\begin{array}{l}{i}_d\\ i_q\\ i_{z1}\\ i_{z2}\\ i_{01}\\ i_{02}\end{array}\right]=P\left[\begin{array}{l}{i}_a\\ i_b\\ i_c\\ i_x\\ i_y\\ i_z\end{array}\right].$$

• $$L_d=L_s+4M_s+3L_m$$ is the stator d-axis inductance.

• $$L_q=L_s+4M_s-3L_m$$ is the stator q-axis inductance.

• $$L_0=L_s-2M_s$$ is the stator zero-sequence inductance.

• ω is the rotor mechanical rotational speed.

• N is the number of rotor permanent magnet pole pairs.

The torque equation is defined by:

$$T=3N\left[i_q\left(i_d{L}_d+{\psi }_m\right)-i_d{i}_q{L}_q\right].$$

Model Thermal Effects

You can expose thermal ports to model the effects of losses that convert power to heat. To expose the thermal ports, set the Modeling option parameter to either:

• No thermal port — The block contains expanded electrical conserving ports associated with the stator windings, but does not contain thermal ports.

• Show thermal port — The block contains expanded electrical conserving ports associated with the stator windings and thermal conserving ports for each of the windings and for the rotor.

For more information about using thermal ports in actuator blocks, see Simulating Thermal Effects in Rotational and Translational Actuators.

Variables

To set the priority and initial target values for the block variables before simulation, use the Initial Targets section in the block dialog box or Property Inspector. For more information, see Set Priority and Initial Target for Block Variables.

Nominal values provide a way to specify the expected magnitude of a variable in a model. Using system scaling based on nominal values increases the simulation robustness. You can specify nominal values using different sources, including the Nominal Values section in the block dialog box or Property Inspector. For more information, see System Scaling by Nominal Values.

Examples

Six-Phase PMSM Torque Control

Control the torque in an electrical-traction drive based on a six-phase permanent magnet synchronous machine (PMSM). A DC voltage source feeds the PMSM through two controlled three-phase converters. The PMSM operates in both motoring and generating modes according to the load. An ideal angular velocity source provides the load. The Control subsystem uses an open-loop approach to control the torque and a closed-loop approach to control the current. At each sample instant, the torque request is converted to a relevant q-axis current reference. The current control is PI-based. The simulation uses several torque steps in both motor and generator modes. The Scopes subsystem contains scopes that allow you to see the simulation results.

• Open Model

Six-Phase PMSM Velocity Control

Control the rotor angular velocity in an electrical-traction drive based on a six-phase permanent magnet synchronous machine (PMSM). A DC voltage source feeds the PMSM through two controlled three-phase converters. The PMSM operates in both motoring and generating modes according to the load. An ideal torque source provides the load. The Scopes subsystem contains scopes that allow you to see the simulation results. The Control subsystem includes a PI-based cascade control structure that has an outer angular-velocity-control loop and four inner current-control loops. During the one second simulation, the angular velocity demand is 0 rpm, 500 rpm, 2000 rpm, and then 3000 rpm.

• Open Model

Ports

Conserving

~ABC — Stator ABC windings

electrical

Three-phase electrical port associated with the stator ABC windings.

~XYZ — Stator XYZ windings

electrical

Three-phase electrical port associated with the stator XYZ windings.

n1 — ABC winding neutral point

electrical

Electrical conserving port associated with the neutral point of the ABC winding configuration.

Dependencies

To enable this port, set Zero sequence to Include.

n2 — XYZ winding neutral point

electrical

Electrical conserving port associated with the neutral point of the XYZ winding configuration.

Dependencies

To enable this port, set Zero sequence to Include.

R — Motor rotor

mechanical rotational

Mechanical rotational conserving port associated with the motor rotor.

C — Motor case

mechanical rotational

Mechanical rotational conserving port associated with the motor case.

HA — a-phase terminal thermal port

thermal

Thermal conserving port associated with stator winding a.

Dependencies

To enable this port, set Modeling option to Show thermal port.

HB — b-phase terminal thermal port

thermal

Thermal conserving port associated with stator winding b.

Dependencies

To enable this port, set Modeling option to Show thermal port.

HC — c-phase terminal thermal port

thermal

Thermal conserving port associated with stator winding c.

Dependencies

To enable this port, set Modeling option to Show thermal port.

HX — x-phase terminal thermal port

thermal

Thermal conserving port associated with stator winding x.

Dependencies

To enable this port, set Modeling option to Show thermal port.

HY — y-phase terminal thermal port

thermal

Thermal conserving port associated with stator winding y.

Dependencies

To enable this port, set Modeling option to Show thermal port.

HZ — z-phase terminal thermal port

thermal

Thermal conserving port associated with stator winding z.

Dependencies

To enable this port, set Modeling option to Show thermal port.

HR — Rotor thermal port

thermal

Thermal conserving port associated with the rotor.

Dependencies

To enable this port, set Modeling option to Show thermal port.

Parameters

Modeling option — Whether to enable thermal ports

No thermal port (default) | Show thermal port

Whether to enable the thermal ports of the block and model the effects of losses that convert power to heat.

Main

Number of pole pairs — Number of pole pairs

6 (default) | scalar

Number of permanent magnet pole pairs on the rotor.

Permanent magnet flux linkage parameterization — Permanent magnet flux linkage parameterization

Specify flux linkage (default) | Specify torque constant | Specify back EMF constant

Permanent magnet flux linkage, specified as Specify flux linkage, Specify torque constant, or Specify back EMF constant.

Permanent magnet flux linkage — Permanent magnet flux linkage

0.03 Wb (default) | scalar

Peak permanent magnet flux linkage for any of the stator windings.

Dependencies

To enable this parameter, set Permanent magnet flux linkage parameterization to Specify flux linkage.

Torque constant — Torque constant

0.18 N*m/A (default) | scalar

Torque constant for any of the stator windings.

Dependencies

To enable this parameter, set Permanent magnet flux linkage parameterization to Specify torque constant.

Back EMF constant — Back EMF constant

0.18 V/(rad/s) (default) | scalar

Back EMF constant for any of the stator windings.

Dependencies

To enable this parameter, set Permanent magnet flux linkage parameterization to Specify back EMF constant.

Stator parameterization — Stator parameterization

Specify Ld, Lq, and L0 (default) | Specify Ls, Lm, and Ms

Stator parameterization, specified as Specify Ld, Lq, and L0 or Specify Ls, Lm, and Ms.

Stator d-axis inductance, Ld — Stator d-axis inductance

0.00019 H (default) | scalar

d-axis inductance.

Dependencies

To enable this parameter, set Stator parameterization to Specify Ld, Lq, and L0.

Stator q-axis inductance, Lq — Stator q-axis inductance

0.00025 H (default) | scalar

q-axis inductance.

Dependencies

To enable this parameter, set Stator parameterization to Specify Ld, Lq, and L0.

Stator zero-sequence inductance, L0 — Stator zero-sequence inductance

0.00016 H (default) | scalar

Zero-sequence inductance.

Dependencies

To enable this parameter, set Stator parameterization to Specify Ld, Lq, and L0.

Stator self-inductance per phase, Ls — Stator self-inductance per phase

0.0002 H (default) | scalar

Average self-inductance of each of the five stator windings.

Dependencies

To enable this parameter, set Stator parameterization to Specify Ls, Lm, and Ms.

Stator inductance fluctuation, Lm — Stator inductance fluctuation

-0.00002 H (default) | scalar

Amount that the self-inductance and mutual inductance of the stator windings fluctuate with the rotor angle.

Dependencies

To enable this parameter, set Stator parameterization to Specify Ls, Lm, and Ms.

Stator mutual inductance, Ms — Stator mutual inductance

0.00002 H (default) | scalar

Average mutual inductance between the stator windings.

Dependencies

To enable this parameter, set Stator parameterization to Specify Ls, Lm, and Ms.

Stator resistance per phase, Rs — Stator resistance per phase

0.013 Ohm (default) | scalar

Resistance of each of the stator windings.

Zero sequence — Zero sequence option

Include (default) | Exclude

Whether to include or exclude zero-sequence terms.

• Include — Include zero-sequence terms. Select this option to prioritize model fidelity. Using this option results in an error for simulations that use the Partitioning solver. For more information, see Increase Simulation Speed Using the Partitioning Solver.

• Exclude — Exclude zero-sequence terms. Select this option to prioritize simulation speed for desktop simulation or real-time deployment, select this option.

Rotor angle definition — Reference point for the rotor angle measurement

Angle between the a-phase magnetic axis and the d-axis (default) | Angle between the a-phase magnetic axis and the q-axis

Reference point for the rotor angle measurement. Motor Construction figure shows the default value, Angle between the a-phase magnetic axis and the d-axis. When you select this value, the rotor and a-phase fluxes aligns when the rotor angle is zero.

When you select Angle between the a-phase magnetic axis and the q-axis, the a-phase current generates maximum torque when the rotor angle is zero.

Mechanical

Rotor inertia — Rotor inertia

0.01 kg*m^2 (default) | nonnegative scalar

Inertia of the rotor attached to the mechanical translational port R. The value can be zero.

Rotor damping — Rotor damping

0 N*m/(rad/s) (default) | nonnegative scalar

Rotary damping.

Thermal

To enable these parameters, set Modeling option to Show thermal port.

Measurement temperature — Rated temperature

298.15 k (default) | real scalar

Temperature for which motor parameters are quoted.

Resistance temperature coefficient — Temperature coefficient

3.93e-3 1/K (default) | positive scalar

Coefficient α in the equation relating resistance to temperature for all three windings, as described in Thermal Model for Actuator Blocks. The default value, 3.93e-3 1/K, is for copper.

Permanent magnet flux temperature coefficient — Permanent magnet flux temperature coefficient

-0.001 1/K (default) | scalar

Fractional rate at which the permanent magnet flux density changes with temperature. Use this parameter to linearly reduce the torque and the induced back EMF as temperature rises.

Thermal mass for each stator winding — Winding thermal mass

100 J/K (default) | positive scalar

Thermal mass value for each stator winding. The thermal mass is the energy required to raise the temperature by one degree.

Rotor thermal mass — Rotor thermal mass

200 J/K (default) | positive scalar

Thermal mass of the rotor. The thermal mass is the energy required to raise the temperature of the rotor by one degree.

References

[1] Krause, Paul, Oleg Wasynczuk, Scott Sudhoff, and Steven Pekarek, eds. Analysis of electric machinery and drive systems. Hoboken, NJ, USA: John Wiley & Sons, Inc., 2013. https://doi.org/10.1002/9781118524336.

[2] Su, Jian Yong, Jin Bo Yang, and Gui Jie Yang. Research on Vector Control and PWM Technique of Six-Phase PMSM. Advanced Materials Research 516–517 (May 2012): 1626–31. https://doi.org/10.4028/www.scientific.net/AMR.516-517.1626.

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.

Version History

Introduced in R2020b