Piezo Bender

Piezoelectric bimorph beam of rectangular cross-section

Since R2021a

• 

Libraries:
Simscape / Electrical / Electromechanical / Mechatronic Actuators

Description

The Piezo Bender block models a piezoeletric bimorph beam of rectangular cross-section.

A piezo bender is a piezoelectric device that bends when you apply an electrical potential between its plates. Conversely, when a piezo bender bends, it generates an electrical potential.

A piezo bender comprises different rectangular layers of piezoelectic material with a polarization perpendicular to the stack. This polarization is alternated in each layer.

Equations

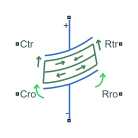
This figure shows the cartesian reference frame

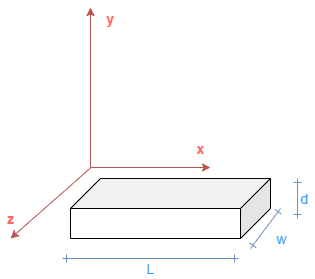
where:

• L is the beam length.

• w is the beam width.

• d is the beam thickness.

These are the constitutive equations for a piezoelectric material in the stress-charge formulation,

$$T=\left[c\right]S-{\left[e\right]}^{T}E$$

(1)

$$D=\left[e\right]S-\left[{ϵ}^S\right]E$$

(2)

where:

• T is the stress field.

• [c] is the compliance tensor.

• S is the strain field.

• [e] is the piezo stress coefficient tensor.

• E is the electric field.

• D is the electric displacement field.

• [ϵ^S] is the permittivity tensor at constant or zero strain.

To model the flexibility, the block uses the Euler-Bernoulli finite-element beam equations. The translation and rotation of each beam cross-section in function of the x-axis determine the beam kinematics.

This block considers only the forces applied in the y direction and the piezoelectric material is polarized to bend only in the x-y plane. For this reason, to describe the kinematics, you only need to specify the vertical displacement in the y direction of the center of gravity of each cross-section, y(x), and the rotation around the z-axis of each cross-section, φ_z(x).

From the previous assumptions, the strain field in an Euler-Bernoulli beam subject to bending is equal to:

$$S_{xx}\left(x,y\right)=-y\frac{d{\phi }_z}{dx}\left(x\right).$$

(3)

Because the electric field is constant between the positive and negative plates, $$E_y=\frac{v}{d}$$, the block substitutes equation 3 into equation 1:

$$T_{xx}\left(x,y\right)=-Ey\frac{d{\phi }_z}{dx}\left(x\right)-e_{31}\frac{v}{d}.$$

In this equation, E = c₁₁ is the Young modulus of the material and e₃₁ is the (3,1) piezoelectric stress-charge coupling coefficient, $${\sigma }_{xx}=-e_{31}{E}_y$$.

This equation defines the bending moment from the stress field:

$$M_z\left(x\right)=-{\displaystyle \iint y{T}_{xx}\left(x,y\right)dS={\displaystyle \iint E{y}^2\frac{d{\phi }_z}{dx}\left(x\right)+e_{31}\frac{v}{d}}}ydS.$$

Because the polarization of the material for $$y=\left[-\frac{d}{2},0\right]$$ is the opposite than the polarization for $$y=\left[0,\frac{d}{2}\right]$$, the (3,1) piezoelectric stress-charge coupling coefficient changes sign and the bending moment is defined by

$$M_z\left(x\right)=\frac{E}{12}w{d}^3\frac{d{\phi }_z}{dx}\left(x\right)+wd{e}_{31}v=EI\frac{d{\phi }_z}{dx}\left(x\right)+wd{e}_{31}v,$$

where $$I=\frac{1}{12}w{d}^3$$ is the second moment of area of the rectangular cross-section.

In this equation, the first term is the classical equation of a beam subject to bending, and the second term is the electromechanical coupling due to the presence of a voltage across the piezoelectric material. This voltage produces a uniform electrical bending moment loaded along the beam.

The block then substitutes equation 3 into equation 2:

$$D_y\left(x,y\right)=-e_{31}y\frac{d{\phi }_z}{dx}\left(x\right)+\frac{ϵv}{d}.$$

The electric charge inside a volume is equal to the Gauss integral of the electric displacement:

$$dq\left(x\right)={\displaystyle ∯D_{y}dS=e_{31}dwdx\frac{d{\phi }_z}{dx}}=e_{31}dwd{\phi }_z.$$

Then, this equation defines the charge accumulated between the two sections of the beam due to the piezoelectric effect:

$$q=e_{31}dw\left({\phi }_z\left(x_2\right)-{\phi }_z\left(x_1\right)\right).$$

Finally, from the mechanical perspective, you can model a piezo bender as an Euler-Bernoulli beam loaded with a uniform torque that is proportional to the voltage:

$$M_z\left(x\right)=EI\frac{d{\phi }_z}{dx}\left(x\right)+wd{e}_{31}v$$

From the electrical perspective, you can model a piezo bender as a capacitor with a charge source proportional to the bending angle:

$$q=e_{31}dw\left({\phi }_{zR}-{\phi }_{zC}\right)+\frac{ϵwl}{d}v.$$

Finite Element Formulation

To discretize and solve the Euler-Bernoulli equations with the piezoelectric coupling, the Piezo Bender block uses a Finite Element method.

The block discretizes the piezo bender beam into a number of slices in the length direction with the same width, w, and thickness, d. The length of each element is equal to the total length of the beam divided by the number of elements, $$l=\frac{L}{N_{elements}}$$.

This stiffness matrix of a finite element of an Euler-Bernoulli beam defines the relationship between the vertical displacement and rotational angle of each end of the beam element, and the corresponding forces and moments due to the beam elasticity:

$$\left[\begin{array}{c}{F}_C\\ T_C\\ F_R\\ T_R\end{array}\right]=\left[\begin{array}{cccc}\frac{12EI}{l^3}& \frac{6EI}{l^2}& -\frac{12EI}{l^3}& \frac{6EI}{l^2}\\ \frac{6EI}{l^2}& \frac{4EI}{l}& -\frac{6EI}{l^2}& \frac{2EI}{l}\\ -\frac{12EI}{l^3}& -\frac{6EI}{l^2}& \frac{12EI}{l^3}& -\frac{6EI}{l^2}\\ \frac{6EI}{l^2}& \frac{2EI}{l}& -\frac{6EI}{l^2}& \frac{4EI}{l}\end{array}\right]\left[\begin{array}{c}{y}_C\\ {\phi }_C\\ y_R\\ {\phi }_R\end{array}\right].$$

Then, to obtain the equations for a piezo bender beam element, add the coupling terms and the mass matrix for the inertia:

$$\frac{\rho lwd}{420}\left[\begin{array}{cccc}156& 22l& 54& -13l\\ 22l& 4l^2& 13l& -3l^2\\ 54& 13l& 156& -22l\\ -13l& -3l^2& -22l& 4l^2\end{array}\right]\left[\begin{array}{c}\frac{d^2{y}_C}{d{t}^2}\\ \frac{d^2{\phi }_C}{d{t}^2}\\ \frac{d^2{y}_R}{d{t}^2}\\ \frac{d^2{\phi }_R}{d{t}^2}\\ 0\end{array}\right]+\left[\begin{array}{ccccc}\frac{12EI}{l^3}& \frac{6EI}{l^2}& -\frac{12EI}{l^3}& \frac{6EI}{l^2}& 0\\ \frac{6EI}{l^2}& \frac{4EI}{l}& -\frac{6EI}{l^2}& \frac{2EI}{l}& e_{31}wd\\ -\frac{12EI}{l^3}& -\frac{6EI}{l^2}& \frac{12EI}{l^3}& -\frac{6EI}{l^2}& 0\\ \frac{6EI}{l^2}& \frac{2EI}{l}& -\frac{6EI}{l^2}& \frac{4EI}{l}& -e_{31}wd\\ 0& -e_{31}wd& 0& e_{31}wd& \frac{ϵwl}{d}\end{array}\right]\left[\begin{array}{c}{y}_C\\ {\phi }_C\\ y_R\\ {\phi }_R\\ v\end{array}\right]=\left[\begin{array}{c}{F}_C\\ T_C\\ F_R\\ T_R\\ q\end{array}\right].$$

Finally, this is the equation for a piezo bender beam element with damping:

$$\frac{\rho lwd}{420}\left[\begin{array}{cccc}156& 22l& 54& -13l\\ 22l& 4l^2& 13l& -3l^2\\ 54& 13l& 156& -22l\\ -13l& -3l^2& -22l& 4l^2\end{array}\right]\left[\begin{array}{c}\frac{d^2{y}_C}{d{t}^2}\\ \frac{d^2{\phi }_C}{d{t}^2}\\ \frac{d^2{y}_R}{d{t}^2}\\ \frac{d^2{\phi }_R}{d{t}^2}\\ 0\end{array}\right]+\left[\begin{array}{ccc}[B]& \cdots & 0\\ ⋮& \ddots & ⋮\\ 0& \cdots & 0\end{array}\right]\left[\begin{array}{c}\frac{d{y}_C}{dt}\\ \frac{d{\phi }_C}{dt}\\ \frac{d{y}_R}{dt}\\ \frac{d{\phi }_R}{dt}\\ 0\end{array}\right]+\left[\begin{array}{ccccc}\frac{12EI}{l^3}& \frac{6EI}{l^2}& -\frac{12EI}{l^3}& \frac{6EI}{l^2}& 0\\ \frac{6EI}{l^2}& \frac{4EI}{l}& -\frac{6EI}{l^2}& \frac{2EI}{l}& e_{31}wd\\ -\frac{12EI}{l^3}& -\frac{6EI}{l^2}& \frac{12EI}{l^3}& -\frac{6EI}{l^2}& 0\\ \frac{6EI}{l^2}& \frac{2EI}{l}& -\frac{6EI}{l^2}& \frac{4EI}{l}& -e_{31}wd\\ 0& -e_{31}wd& 0& e_{31}wd& \frac{ϵwl}{d}\end{array}\right]\left[\begin{array}{c}{y}_C\\ {\phi }_C\\ y_R\\ {\phi }_R\\ v\end{array}\right]=\left[\begin{array}{c}{F}_C\\ T_C\\ F_R\\ T_R\\ q\end{array}\right]$$

where:

• l is the element length.

• w is the element width.

• d is the element thickness.

• $$I=\frac{1}{12}w{t}^3$$ is the second moment of area.

• E is the Young modulus.

• m = ρlwd is the element mass, where ρ is the mass density.

• e₃₁ is the (3,1) piezoelectric stress-charge coupling coefficient, $${\sigma }_{xx}=-e_{31}{E}_y$$.

• ε is the electrical permittivity.

• $$B=b_{k}K+b_{m}M$$ is the damping matrix.

• b_m is the Rayleigh damping coefficient proportional to mass.

• b_k is the Rayleigh damping coefficient proportional to stiffness.

• $$K=\left[\begin{array}{cccc}\frac{12EI}{l^3}& \frac{6EI}{l^2}& -\frac{12EI}{l^3}& \frac{6EI}{l^2}\\ \frac{6EI}{l^2}& \frac{4EI}{l}& -\frac{6EI}{l^2}& \frac{2EI}{l}\\ -\frac{12EI}{l^3}& -\frac{6EI}{l^2}& \frac{12EI}{l^3}& -\frac{6EI}{l^2}\\ \frac{6EI}{l^2}& \frac{2EI}{l}& -\frac{6EI}{l^2}& \frac{4EI}{l}\end{array}\right]$$ is the stiffness finite element matrix.

• $$M=\frac{\rho lwd}{420}\left[\begin{array}{cccc}156& 22l& 54& -13l\\ 22l& 4l^2& 13l& -3l^2\\ 54& 13l& 156& -22l\\ -13l& -3l^2& -22l& 4l^2\end{array}\right]$$ is the mass matrix.

• y_C is the deflection along the y-axis of the left-end of the element.

• y_R is the deflection along the y-axis of the right-end of the element.

• φ_C is the rotation around the z-axis of the left-end of the element.

• φ_R is the rotation around the z-axis of the right-end of the element.

• F_C is the force along the y-axis of the left-end of the element.

• F_R is the force along the y-axis of the right-end of the element.

• T_C is the torque in the z-axis of the left-end of the element.

• T_R is the torque in the z-axis of the right-end of the element.

• v is the voltage across the top and bottom electrodes.

• q is the accumulated charge between the electrodes and the piezoelectric material.

Datasheet Parameterization

A datasheet of a piezo bender usually provides this data:

• Dimensions (l, w, d)

• Mass, m

• Rated voltage, v_rated

• Free deflection at rated voltage, y_free

• Blocking force at rated voltage, F_block

• Capacitance, C_piezo

• First resonant frequency, f₁

It is possible to calculate the fundamental material parameters of a piezo bender by using the datasheet parameters.

First, the block solves the voltage-force deflection relationships from the steady-state equations with no torque applied and clamped-free configuration:

$$\left[\begin{array}{ccc}\frac{12EI}{l^3}& -\frac{6EI}{l^2}& 0\\ -\frac{6EI}{l^2}& \frac{4EI}{l}& -e_{31}wd\\ 0& e_{31}wd& \frac{\epsilon wl}{d}\end{array}\right]\left[\begin{array}{c}{y}_R\\ {\phi }_R\\ v\end{array}\right]=\left[\begin{array}{c}{F}_R\\ 0\\ q\end{array}\right].$$

These equations define the relationship between the tip deflection, voltage and tip force:

$$\begin{array}{l}{y}_R=\frac{l^2(4F_{R}l+6dw{e}_{31}v)}{12EI}=\frac{l^2(4F_{R}l+6dw{e}_{31}v)}{Ew{d}^3}=F_R\frac{4l^3}{Ew{d}^3}+v\frac{6e_{31}{l}^2}{E{d}^2}\\ y_{free}=\frac{6l^{2}dw{e}_{31}{v}_{rated}}{12EI}=\frac{6e_{31}{l}^2{v}_{rated}}{E{d}^2}\\ F_{block}=-\frac{3dw{e}_{31}{v}_{rated}}{2l}\end{array}$$

The block computes the capacitance by assuming zero applied force:

$$C_{piezo}=\epsilon \frac{lw}{d}+e_{31}^2\frac{l{d}^2{w}^2}{EI}=\epsilon \frac{lw}{d}+e_{31}^2\frac{12lw}{Ed}=\left(\epsilon +12\frac{e_{31}^2}{E}\right)\frac{lw}{d}.$$

Finally, this equation shows the relationship between density and mass:

$$m=\rho lwd.$$

Once you have defined all the relationships between the fundamental and datasheet parameters, you can calculate the fundamental parameters with these equations:

$$\begin{array}{l}{e}_{31}=-\frac{2l{F}_{block}}{3dw{v}_{rated}}\\ E=-\frac{4F_{block}{l}^3}{y_{free}{d}^{3}w}\\ \epsilon =\frac{d}{lw}\left(C_{piezo}+\frac{4F_{block}{y}_{free}}{v_{rated}^2}\right)\end{array}$$

Then substitute these equations in the constitutive equations:

$$\begin{array}{l}\frac{v}{v_{rated}}=\frac{F_R}{F_{block}}+\frac{y_R}{y_{free}}\\ q=C_{piezo}v+\frac{y_{free}}{v_{rated}}{F}_R\end{array}$$

Dynamics Datasheet Parameterization

You can calculate the first resonance frequency of a clamped-free beam of uniform cross section by using this equation:

$$2\pi f_0={1.855}^2\sqrt{\frac{EI}{m{l}^3}}.$$

The block then parameterizes the dynamics directly by specifying the desired natural frequency.

Boundary Conditions

Beams have different boundary conditions at their left and right ends:

• Free — Both the displacement and rotation are equal to any value.

• Simply supported — The displacement is equal to 0.

• Clamped — Both the displacement and rotation are equal to 0.

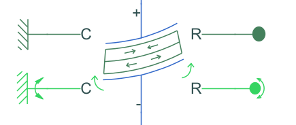
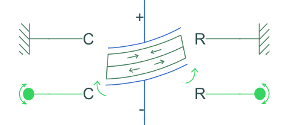
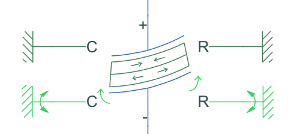
This table shows the possible boundary configurations for a piezo bender beam.

Configuration	Model
Clamped-free
Supported-supported
Clamped-clamped

Examples

Piezo Bender Energy Harvester

Model a device that harvests energy from a vibrating object by using a piezo bender. The device uses this energy to charge a battery and power a load.

Open Model

Ports

Conserving

+ — Positive terminal

electrical

Electrical conserving port associated with the piezo bender positive terminal.

- — Negative terminal

electrical

Electrical conserving port associated with the piezo bender negative terminal.

Ctr — Translational case

mechanical

Mechanical translational conserving port associated with the case.

Cro — Rotational case

mechanical

Mechanical rotational conserving port associated with the case.

Rtr — Translational rotor

mechanical

Mechanical translational conserving port associated with the rotor.

Rro — Rotational rotor

mechanical

Mechanical rotational conserving port associated with the rotor.

Parameters

Dimensions

Number of elements — Number of elements

1 (default) | positive integer greater than or equal to 1

Number of elements in which the piezo bender beam is discretized using the Euler-Bernoulli finite elements equations.

Total beam length — Total beam length

3.175E-2 m (default) | positive scalar

Total length of the beam.

Beam width — Beam width

1.27E-2 m (default) | positive scalar

Width of the beam.

Beam thickness — Beam thickness

5.08E-4 m (default) | positive scalar

Thickness of the beam.

Steady-State

Parameterization — Steady-state parameterization

Specify from a datasheet for clamped-free configuration (default) | Specify from material properties

Whether to parameterize the steady state parameters from a datasheet or from material properties.

Capacitance — Piezo bender capacitance

15 nF (default) | positive scalar

Capacitance of the piezo bender.

Dependencies

To enable this parameter, set Parameterization to Specify from a datasheet for clamped-free configuration.

Rated drive voltage, Vrated — Rated drive voltage

180 V (default) | positive scalar

Rated drive voltage.

Dependencies

To enable this parameter, set Parameterization to Specify from a datasheet for clamped-free configuration.

Free deflection at Vrated — Free deflection at Vrated

+0.233 mm (default) | nonzero value

Tip deflection when no force is applied. The sign of this parameter must be different from the sign of the Blocking force at Vrated parameter.

Dependencies

To enable this parameter, set Parameterization to Specify from a datasheet for clamped-free configuration.

Blocking force at Vrated — Blocking force at Vrated

-0.414 N (default) | scalar

Force that nullifies the tip deflection. The sign of this parameter must be different from the sign of the Free deflection at Vrated parameter.

Dependencies

To enable this parameter, set Parameterization to Specify from a datasheet for clamped-free configuration.

Young modulus, E — Young modulus

1.36628e11 N/m^2 (default) | positive scalar

Young modulus, or the modulus of elasticity in tension.

Dependencies

To enable this parameter, set Parameterization to Specify from material properties.

Piezoelectric stress coefficient, e31 — Piezoelectric stress coefficient

7.5459 C/m^2 (default) | nonzero scalar

(3,1) piezoelectric stress-charge coupling coefficient.

Dependencies

To enable this parameter, set Parameterization to Specify from material properties.

Dielectric constant — Dielectric constant

1.38965e-08 F/m (default) | positive scalar

Dielectric constant that represents the relative permittivity of the material. This parameter must be bigger than the vacuum permittivity.

Dependencies

To enable this parameter, set Parameterization to Specify from material properties.

Dynamics

Inertial effects — Inertial effects modeling option

On (default) | Off

Whether to model inertial effects.

Parameterization — Inertia parameterization

Specify from a datasheet for clamped-free configuration (default) | Specify from material properties

Whether to parameterize the inertia parameters from a datasheet or from material properties.

Dependencies

To enable this parameter, set Inertial effects to On.

Beam mass — Beam mass

1.6 g (default) | positive scalar

Mass of the beam.

Dependencies

To enable this parameter, set Inertial effects to On and Parameterization to Specify from material properties.

First natural frequency — First natural frequency

391 Hz (default) | positive scalar

First natural frequency.

Dependencies

To enable this parameter, set Inertial effects to On and Parameterization to Specify from a datasheet for clamped-free configuration.

Rayleigh damping constant proportional to stiffness — Rayleigh damping constant proportional to stiffness

1e-5 s (default) | nonnegative scalar

Damping coefficient proportional to stiffness, for Rayleigh damping.

Rayleigh damping constant proportional to mass — Rayleigh damping constant proportional to mass

0 1/s (default) | nonnegative scalar

Damping coefficient proportional to mass, for Rayleigh damping.

Dependencies

To enable this parameter, set Inertial effects to On.

References

[1] Tadmor, E. B., and G. Kosa. "Electromechanical Coupling Correction for Piezoelectric Layered Beams." Journal of Microelectromechanical Systems, vol. 12, no. 6, Dec. 2003, pp. 899–906. DOI.org (Crossref), doi:10.1109/JMEMS.2003.820286.

[2] Benjeddou A, Trindade MA, Ohayon R. "A Unified Beam Finite Element Model for Extension and Shear Piezoelectric Actuation Mechanisms." Journal of Intelligent Material Systems and Structures. 1997;8(12):1012-1025. doi:10.1177/1045389X9700801202

[3] Gavin, Henri P. "Beam Element Stiffness Matrices." CEE 421L. Matrix Structural Analysis. Duke University, 2014.

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.

Version History

Introduced in R2021a