Model Reference Adaptive Controller
Discrete-time PID-based model reference adaptive control
Libraries:
Simscape /
Electrical /
Control /
General Control
Description
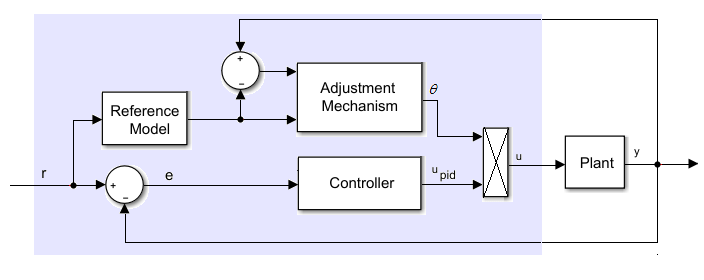
The Model Reference Adaptive Controller block implements discrete-time proportional-integral-derivative (PID) model reference adaptive control (MRAC). The three main components of an MRAC system are the reference model, the adjustment mechanism, and the controller.
Equations
The control equation is
where:
upid is the controller output.
Kp is the proportional gain.
Ki is the integral gain.
Kd is the differential gain.
Ts is the sample time.
e is the error.
The reference model is the transfer function for the closed-loop system. This model captures the desired behavior of the closed-loop system. It is implemented as the discrete-time transfer function
The adaptation mechanism adjusts the control action based on the error between the plant output and the reference model output as
where:
θ is the adaptation parameter.
y is the plant output.
ym is the reference model output.
γ is the learning rate.
Increasing the value of γ results in faster adaptation to plant changes.
The adjusted control signal, u, is
Ports
Input
Output
Parameters
References
[1] Butler, H. Model-Reference Adaptive Control-From Theory to Practice. Upper Saddle River, NJ: Prentice Hall, 1992.
Extended Capabilities
Version History
Introduced in R2018a