Simplified Synchronous Machine
(To be removed) Model the dynamics of simplified three-phase synchronous machine
The Specialized Power Systems library will be removed in R2026a. Use the Simscape™ Electrical™ blocks and functions instead. For more information on updating your models, see Upgrade Specialized Power System Models to use Simscape Electrical Blocks.
Libraries:
Simscape /
Electrical /
Electromechanical /
Synchronous
Description
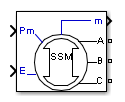
The Simplified Synchronous Machine block models both the electrical and mechanical characteristics of a simple synchronous machine.
The electrical system for each phase consists of a voltage source in series with an RL impedance, which implements the internal impedance of the machine. The value of R can be zero but the value of L must be positive.
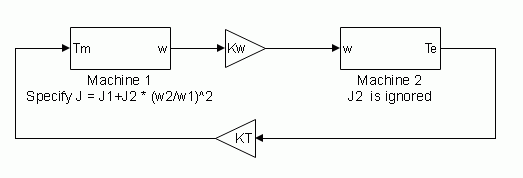
The Simplified Synchronous Machine block implements the mechanical system described by
where
| Δω = Speed variation with respect to speed of
operation H = constant of inertia Tm = mechanical torque Te = electromagnetic torque Kd = damping factor representing the effect of damper windings ω(t) = mechanical speed of the rotor ω0 = speed of operation (1 p.u.) | (1) |
Although the parameters can be entered in either SI units or per unit in the dialog box, the internal calculations are done in per unit. The following block diagram illustrates how the mechanical part of the model is implemented. The model computes a deviation with respect to the speed of operation; not the absolute speed itself.

The Kd damping coefficient simulates the effect of damper windings normally used in synchronous machines. When the machine is connected to an infinite network (zero impedance), the variation of machine power angle delta (δ) resulting from a change of mechanical power (Pm) can be approximated by the following second-order transfer function:
where
δ | Power angle delta: angle of internal voltage E with respect to terminal voltage, in radians |
Pm | Mechanical power in pu |
ωn | Frequency of electromechanical oscillations = in rad/s |
ζ | Damping ratio = |
ωs | Electrical frequency in rad/s |
Pmax | Maximum power in pu transmitted through reactance X at terminal voltage Vt and internal voltage E. Pmax = VtE/X, where Vt, E, and X are in pu |
H | Inertia constant(s) |
Kd | Damping factor (pu_of_torque / pu_of_speed) |
This approximate transfer function, which has been derived by assuming sin(δ) = δ, is valid for small power angles (δ < 30 degrees). It follows from the preceding ζ expression that the Kd value required to obtain a given ζ damping ratio:
Assumptions and Limitations
The electrical system of the Simplified Synchronous Machine block consists solely of a voltage source behind a synchronous reactance and resistance. All the other self- and magnetizing inductances of the armature, field, and damping windings are neglected. The effect of damper windings is approximated by the damping factor Kd. The three voltage sources and RL impedance branches are Y-connected (three wires or four wires). The load might or might not be balanced.
When you use Simplified Synchronous Machine blocks in discrete systems, you might have to use a small parasitic resistive load, connected at the machine terminals, to avoid numerical oscillations. Large sample times require larger loads. The minimum resistive load is proportional to the sample time. Remember that with a 25 μs time step on a 60 Hz system, the minimum load is approximately 2.5% of the machine nominal power. For example, a 200 MVA simplified synchronous machine in a power system discretized with a 50 μs sample time requires approximately 5% of resistive load or 10 MW. If the sample time is reduced to 20 μs, a resistive load of 4 MW should be sufficient.
Ports
Input
Output
Conserving
Parameters
Extended Capabilities
Version History
Introduced before R2006a