Model Gain-Scheduled Control Systems in Simulink
In Simulink®, you can model gain-scheduled control systems in which controller gains or coefficients depend on scheduling variables such as time, operating conditions, or model parameters. The library of linear parameter-varying blocks in Control System Toolbox™ lets you implement common control-system elements with variable gains. Use blocks such as lookup tables or MATLAB Function blocks to implement the gain schedule, which gives the dependence of these gains on the scheduling variables.
To model a gain-scheduled control system in Simulink:
Identify the scheduling variables and the signals that represent them in your model. For instance, if your system is a cruising aircraft, then the scheduling variables might be the incidence angle and the airspeed of the aircraft.
Use a lookup table block or a MATLAB Function block to implement a gain or coefficient that depends on the scheduling variables. If you do not have lookup table values or MATLAB® expressions for gain schedules that meet your performance requirements, you can use
systuneto tune them. See Tune Gain Schedules in Simulink.Replace ordinary control elements with gain-scheduled elements. For instance, instead of a fixed-coefficient PID controller, use a Varying PID Controller block, in which the gain schedules determine the PID gains.
Add scheduling logic and safeguards to your model as needed.
Model Scheduled Gains
A gain schedule converts the current values of the scheduling variables into controller gains. There are several ways to implement a gain schedule in Simulink.
Available blocks for implementing lookup tables include:
Lookup tables — A lookup table is a list of breakpoints and corresponding gain values. When the scheduling variables fall between breakpoints, the lookup table interpolates between the corresponding gains. Use the following blocks to implement gain schedules as lookup tables.
1-D Lookup Table, 2-D Lookup Table, n-D Lookup Table — For a scalar gain that depends on one, two, or more scheduling variables.
Matrix Interpolation — For a matrix-valued gain that depends on one, two, or three scheduling variables. (This block is in the Simulink Extras library.)
MATLAB Function block — When you have a functional expression relating the gains to the scheduling variables, use a MATLAB Function block. If the expression is a smooth function, using a MATLAB function can result in smoother gain variations than a lookup table. Also, if you use a code-generation product such as Simulink Coder™ to implement the controller in hardware, a MATLAB function can result in a more memory-efficient implementation than a lookup table.
You can use
systune to tune gain schedules implement as either lookup tables or
MATLAB functions. See Tune Gain Schedules in Simulink.
Scheduled Gain in Controller
As an example, the model rct_CSTR includes a PI controller and a
lead compensator in which the controller gains are implemented as lookup tables using
1-D Lookup Table blocks. For more
information on this model, see Gain-Scheduled Control of a Chemical Reactor.
Copy the example files and open the rct_CSTR model.
openExample("control/GainScheduledProcessExample",... supportingFile="rct_CSTR.slx")

Both the Concentration controller and Temperature
controller blocks take the CSTR plant output,
Cr, as an input. This value is both the controlled variable of the
system and the scheduling variable on which the controller action depends. Double-click
the Concentration controller block.
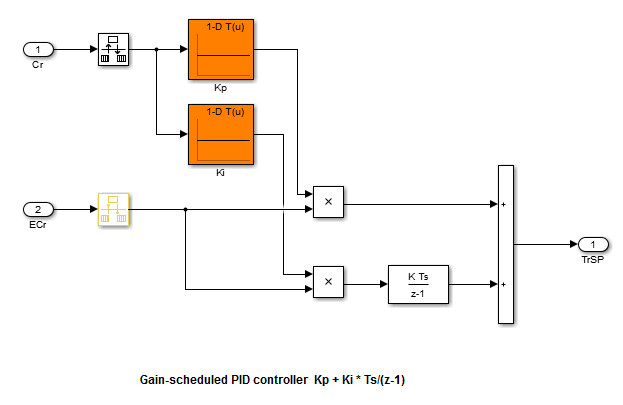
This block is a PI controller in which the proportional gain Kp and
integrator gain Ki are determined by feeding the scheduling parameter
Cr into a 1-D Lookup Table block. Similarly, the
Temperature controller block contains three gains implemented as
lookup tables.
Gain-Scheduled Equivalents for Commonly Used Control Elements
Use the Linear Parameter Varying block library of Control System Toolbox to implement common control elements with variable parameters or coefficients. These blocks provide common elements in which the gains or parameters are available as external inputs. The following table lists some applications of these blocks.
| Block | Application |
|---|---|
| Use these blocks to implement a Butterworth lowpass filter in which the cutoff frequency varies with scheduling variables. | |
| Use these blocks to implement a notch filter in which the notch frequency, width, and depth vary with scheduling variables. | |
| These blocks are preconfigured versions of the PID Controller and PID Controller (2DOF) blocks. Use them to implement PID controllers in which the PID gains vary with scheduling variables. |
| Use these blocks to implement a transfer function of any order in which the polynomial coefficients of the numerator and denominator vary with scheduling variables. | |
| Use these blocks to implement a state-space controller in which the A, B, C, and D matrices vary with the scheduling variables. | |
| Use these blocks to implement a gain-scheduled observer-form state-space controller, such as an LQG controller. In such a controller, the A, B, C, D matrices and the state-feedback and state-observer gain matrices vary with the scheduling variables. |
Gain-Scheduled Notch Filter
For example, the subsystem in the following illustration uses a Varying Notch Filter block to implement a filter whose notch frequency varies as a function of two scheduling variables. The relationship between the notch frequency and the scheduling variables is implemented in a MATLAB function.

Gain-Scheduled PI Controller
As another example, the following subsystem is a gain-scheduled discrete-time PI controller in which both the proportional and integral gains depend on the same scheduling variable. This controller uses 1-D Lookup Table blocks to implement the gain schedules.

Matrix-Valued Gain Schedules
You can also implement matrix-valued gain schedules Simulink. A matrix-valued gain schedule takes one or more scheduling variables and returns a matrix rather than a scalar value. For instance, suppose that you want to implement a time-varying LQG controller of the form:
where, in general, the state-space matrices A, B, C, and D, the state-feedback matrix K, and the observer-gain matrix L all vary with time. In this case, time is the scheduling variable, and the gain schedule determines the values of the matrices at a given time.
In your Simulink model, you can implement matrix-valued gain schedules using:
MATLAB Function block — Specify a MATLAB function that takes scheduling variables and returns matrix values.
Matrix Interpolation block — Specify a lookup table to associate a matrix value with each scheduling-variable breakpoint. Between breakpoints, the block interpolates the matrix elements. (This block is in the Simulink Extras library.)
For the LQG controller, use either MATLAB Function blocks or Matrix Interpolation blocks to implement the time-varying matrices as inputs to a Varying Observer Form block. For example:

In this implementation, the time-varying matrices are each implemented as a MATLAB Function block in which the associated function takes the simulation time and returns a matrix of appropriate dimensions.
You can tune
matrix-valued gain schedules implemented as either MATLAB Function blocks
or as Matrix Interpolation blocks. However, to tune a Matrix
Interpolation block, you must set Simulate using to
Interpreted execution. See the Matrix Interpolation block reference
page for information about simulation modes.
Avoiding Algebraic Loops
When using these parameter-varying blocks, avoid scheduling the system coefficients or state-space matrices based on the system output y (or control signal u for the observer-form blocks). If you have such dependence, the resulting system creates an algebraic loop, because computing the block output value y (or u) requires knowing the output value. This algebraic loop is prone to instability and divergence. Instead, try expressing the coefficients or matrices in terms of the time t, the block input u, and state outputs x.
For similar reasons, when using the varying state-space block, avoid scheduling A and B based on the dx or xk+1 outputs. Note that it is safe to for A and B to depend on y when y is a fixed combination of states and inputs, (in other words, when y = Cx + Du where C and D are constant matrices).
Similarly, in the discrete-time varying state-space block, avoid using xk+1 to schedule A and B. You can use yk to schedule A and B when yk is a fixed combination of states and inputs.
For more information about algebraic loops, see Algebraic Loop Concepts.
Custom Gain-Scheduled Control Structures
You can also use the scheduled gains to build your own control elements. For example,
the model rct_CSTR includes a gain-scheduled lead compensator with three
coefficients that depend on the scheduling variable, CR. To see how this
compensator is implemented, open the model and examine the Temperature
controller subsystem.

Here, the overall gain Kt, the zero location a,
and the pole location b are each implemented as a 1-D lookup table that
takes the scheduling variable as input. The lookup tables feed directly into product blocks.
Tunability of Gain Schedules
For a lookup table or MATLAB Function block that implements a gain
schedule to be tunable with systune, it must ultimately feed into
either:
A block in the Linear Parameter Varying block library.
A Product block that applies the gain to a given signal. For instance, if the Product block takes as inputs a scheduled gain g(α) and a signal u(t), then the output signal of the block is y(t) = g(α)u(t).
There can be one or more of the following blocks between the lookup table or MATLAB Function block and the Product block or parameter-varying block:
Gain
Bias
Blocks that are equivalent to a unit gain in the linear domain, including:
Transport Delay, Variable Transport Delay
Saturate, Deadzone
Rate Limiter, Rate Transition
Quantizer, Memory, Zero-Order Hold
MinMax
Data Type Conversion
Signal Specification
Switch blocks, including:
Switch
Multiport Switch
Manual Switch
Inserting such blocks can be useful, for example, to constrain the gain value to a certain range, or to specify how often the gain schedule is updated.