OptimResults
Estimation results object for any supported algorithm except
nlinfit
Description
The OptimResults object contains estimation results from
fitting a SimBiology® model to data using the sbiofit function with any supported
algorithm except nlinfit. See the sbiofit function for a list of supported algorithms.
Creation
Use sbiofit with any supported estimation algorithm
except nlinfit to create an OptimResults object.
Properties
Name of the group associated with the results, specified as a categorical. If the
'Pooled' name-value pair argument was set to
true when you ran sbiofit, then
GroupName is returned as an empty array or
[].
Table of estimated parameters, specified as a table. The jth
row of the table represents the jth estimated parameter
βj. It contains transformed values of
parameter estimates if any parameter transform is specified. Standard errors of these
parameter estimates (StandardError) are calculated as:
sqrt(diag(COVB)).
It can also contain the following variables:
Bounds— the values of transformed parameter bounds that you specified during fittingCategoryVariableName— the names of categories or groups that you specified during fittingCategoryValue— the values of category variables specified byCategoryVariableName
This table contains one row per distinct parameter value.
Table of estimated parameters, specified as a table. The jth
row of the table represents the jth estimated parameter
βj. This table contains untransformed
values of parameter estimates. Standard errors of these parameter estimates
(StandardError) are calculated as:
sqrt(diag(CovarianceMatrix)).
It can also contain the following variables:
Bounds— the values of transformed parameter bounds that you specified during fittingCategoryVariableName— the names of categories or groups that you specified during fittingCategoryValue— the values of category variables specified byCategoryVariableName
This table contains sets of parameter values that are identified for each individual or group.
Jacobian matrix of the model, specified as an array. The Jacobian matrix with respect to an estimated parameter is
where ti is the ith time point, βj is the jth estimated parameter in the transformed space, and yk is the kth response in the group of data.
Estimated covariance matrix for Beta, specified as a matrix. This
matrix is calculated as: COVB = inv(J'*J)*MSE.
Estimated covariance matrix for ParameterEstimates, specified as
a matrix. This matrix is calculated as: CovarianceMatrix = T'*COVB*T,
where T = diag(JInvT(Beta)). JInvT(Beta) returns a
Jacobian matrix of Beta which is inverse transformed accordingly if
you specified any transform to estimated parameters.
For instance, suppose you specified the log-transform for an estimated parameter
x when you ran sbiofit. The inverse transform is: InvT = exp(x), and
its Jacobian is: JInvT = exp(x) since the derivative of
exp is also exp.
Residuals matrix, specified as a matrix. Rij is the residual for the ith time point and the jth response in the group of data.
Maximized loglikelihood for the fitted model, specified as a scalar.
Akaike Information Criterion (AIC), specified as a scalar. The AIC is calculated as
AIC = 2*(-LogLikelihood + P), where P is the
number of parameters.
Bayes Information Criterion (BIC), specified as a scalar. The BIC is calculated as
BIC = -2*LogLikelihood + P*log(N), where N is
the number of observations, and P is the number of parameters.
Degrees of freedom for error (DFE), specified as a scalar. The DFE is calculated as
DFE = N-P, where N is the number of observations
and P is the number of parameters.
Mean squared error, specified as a scalar.
Sum of squared (weighted) errors or residuals, specified as a scalar.
Matrix of weights, specified as a matrix with one column per response and one row per observation.
Data used for fitting, specified as a groupedData object.
In most cases, this Data property contains
a copy of groupedData specified as the input data in the
sbiofit call or the Data property of
a fitproblem object.
One exception is that the Data property of unpooled fit results objects
contain only the subset of data for the individual group used for fitting.
Estimated parameter names, specified as a cell array of character vectors.
Error models and estimated error model parameters, specified as a table.
The table has one row per error model.
The
ErrorModelInfo.Properties.RowsNamesproperty identifies which responses the row applies to.The table contains three variables:
ErrorModel,a, andb. TheErrorModelvariable is categorical. The variablesaandbcan beNaNwhen they do not apply to a particular error model.
There are four built-in error models. Each model defines the error using a standard mean-zero and unit-variance (Gaussian) variable e, the function value f, and one or two parameters a and b. In SimBiology, the function f represents simulation results from a SimBiology model.
'constant':'proportional':'combined':'exponential':
Name of the estimation function, specified as a character vector.
File names to include for deployment, specified as a cell array of character vectors.
Exit flag specific to the estimation function, specified as a scalar. See the
reference page of the specific algorithm to get more information on the value of
ExitFlag.
Additional outputs specific to the estimation function, specified as a structure
array. See the reference page of the specific algorithm to get more information on the
values of the Output structure array.
Object Functions
boxplot | Create box plot showing the variation of estimated SimBiology model parameters |
fitted | Return simulation results of SimBiology model fitted using least-squares regression |
plot | Compare simulation results to the training data, creating a time-course subplot for each group |
plotActualVersusPredicted | Compare predictions to actual data, creating a subplot for each response |
plotResidualDistribution | Plot the distribution of the residuals |
plotResiduals | Plot residuals for each response, using time, group, or prediction as x-axis |
predict | Simulate and evaluate fitted SimBiology model |
random | Simulate SimBiology model, adding variations by sampling error model |
summary | Return structure array that contains estimated values and fit quality statistics |
Examples
Background
This example shows how to fit an individual's PK profile data to one-compartment model and estimate pharmacokinetic parameters.
Suppose you have drug plasma concentration data from an individual and want to estimate the volume of the central compartment and the clearance. Assume the drug concentration versus the time profile follows the monoexponential decline , where is the drug concentration at time t, is the initial concentration, and is the elimination rate constant that depends on the clearance and volume of the central compartment .
The synthetic data in this example was generated using the following model, parameters, and dose:
One-compartment model with bolus dosing and first-order elimination
Volume of the central compartment (
Central) = 1.70 literClearance parameter (
Cl_Central) = 0.55 liter/hourConstant error model
Bolus dose of 10 mg
Load Data and Visualize
The data is stored as a table with variables Time and Conc that represent the time course of the plasma concentration of an individual after an intravenous bolus administration measured at 13 different time points. The variable units for Time and Conc are hour and milligram/liter, respectively.
load('data15.mat') plot(data.Time,data.Conc,'b+') xlabel('Time (hour)'); ylabel('Drug Concentration (milligram/liter)');

Convert to groupedData Format
Convert the data set to a groupedData object, which is the required data format for the fitting function sbiofit for later use. A groupedData object also lets you set independent variable and group variable names (if they exist). Set the units of the Time and Conc variables. The units are optional and only required for the UnitConversion feature, which automatically converts matching physical quantities to one consistent unit system.
gData = groupedData(data);
gData.Properties.VariableUnits = {'hour','milligram/liter'};
gData.Propertiesans = struct with fields:
Description: ''
UserData: []
DimensionNames: {'Row' 'Variables'}
VariableNames: {'Time' 'Conc'}
VariableTypes: ["double" "double"]
VariableDescriptions: {}
VariableUnits: {'hour' 'milligram/liter'}
VariableContinuity: []
RowNames: {}
CustomProperties: [1×1 matlab.tabular.CustomProperties]
GroupVariableName: ''
IndependentVariableName: 'Time'
groupedData automatically set the name of the IndependentVariableName property to the Time variable of the data.
Construct a One-Compartment Model
Use the built-in PK library to construct a one-compartment model with bolus dosing and first-order elimination where the elimination rate depends on the clearance and volume of the central compartment. Use the configset object to turn on unit conversion.
pkmd = PKModelDesign; pkc1 = addCompartment(pkmd,'Central'); pkc1.DosingType = 'Bolus'; pkc1.EliminationType = 'linear-clearance'; pkc1.HasResponseVariable = true; model = construct(pkmd); configset = getconfigset(model); configset.CompileOptions.UnitConversion = true;
For details on creating compartmental PK models using the SimBiology® built-in library, see Create Pharmacokinetic Models.
Define Dosing
Define a single bolus dose of 10 milligram given at time = 0. For details on setting up different dosing schedules, see Doses in SimBiology Models.
dose = sbiodose('dose'); dose.TargetName = 'Drug_Central'; dose.StartTime = 0; dose.Amount = 10; dose.AmountUnits = 'milligram'; dose.TimeUnits = 'hour';
Map Response Data to the Corresponding Model Component
The data contains drug concentration data stored in the Conc variable. This data corresponds to the Drug_Central species in the model. Therefore, map the data to Drug_Central as follows.
responseMap = {'Drug_Central = Conc'};Specify Parameters to Estimate
The parameters to fit in this model are the volume of the central compartment (Central) and the clearance rate (Cl_Central). In this case, specify log-transformation for these biological parameters since they are constrained to be positive. The estimatedInfo object lets you specify parameter transforms, initial values, and parameter bounds if needed.
paramsToEstimate = {'log(Central)','log(Cl_Central)'};
estimatedParams = estimatedInfo(paramsToEstimate,'InitialValue',[1 1],'Bounds',[1 5;0.5 2]);Estimate Parameters
Now that you have defined one-compartment model, data to fit, mapped response data, parameters to estimate, and dosing, use sbiofit to estimate parameters. The default estimation function that sbiofit uses will change depending on which toolboxes are available. To see which function was used during fitting, check the EstimationFunction property of the corresponding results object.
fitConst = sbiofit(model,gData,responseMap,estimatedParams,dose);
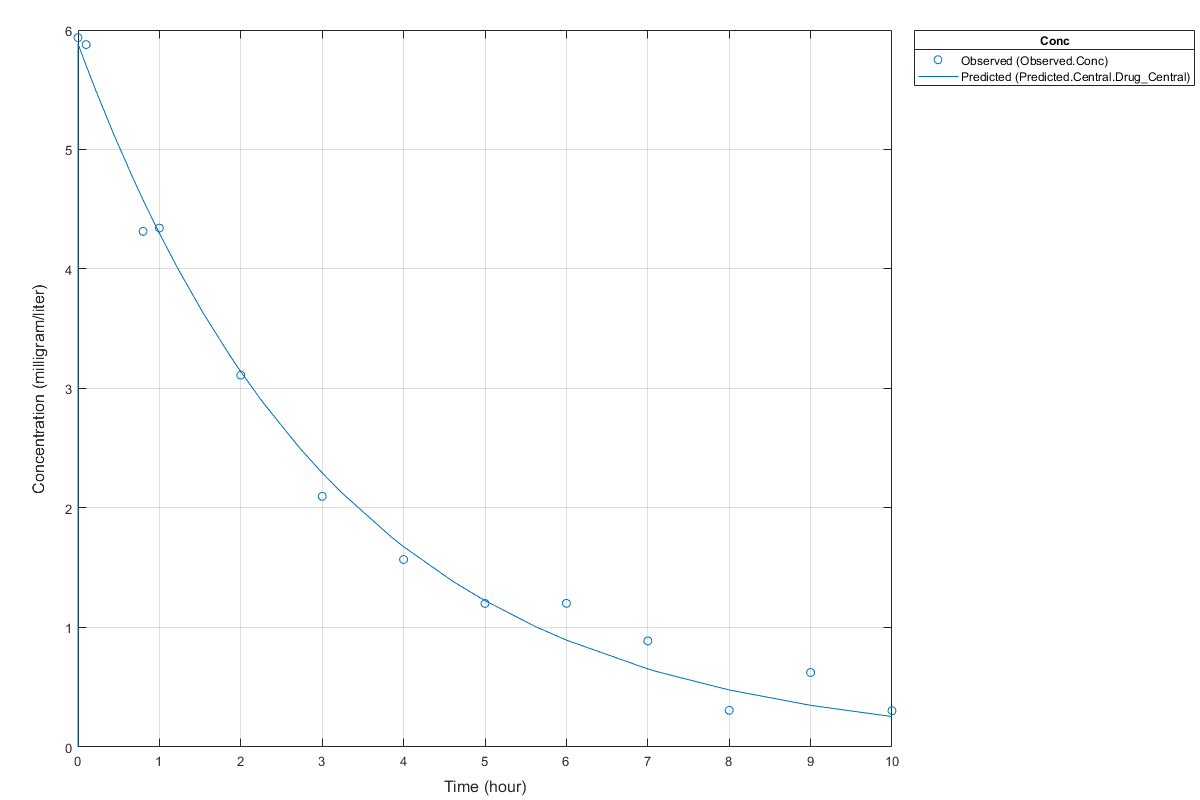
Display Estimated Parameters and Plot Results
Notice the parameter estimates were not far off from the true values (1.70 and 0.55) that were used to generate the data. You may also try different error models to see if they could further improve the parameter estimates.
fitConst.ParameterEstimates
ans=2×4 table
Name Estimate StandardError Bounds
______________ ________ _____________ __________
{'Central' } 1.6993 0.034821 1 5
{'Cl_Central'} 0.53358 0.01968 0.5 2
s.Labels.XLabel = 'Time (hour)'; s.Labels.YLabel = 'Concentration (milligram/liter)'; plot(fitConst,'AxesStyle',s);
Use Different Error Models
Try three other supported error models (proportional, combination of constant and proportional error models, and exponential).
fitProp = sbiofit(model,gData,responseMap,estimatedParams,dose,... 'ErrorModel','proportional'); fitExp = sbiofit(model,gData,responseMap,estimatedParams,dose,... 'ErrorModel','exponential'); fitComb = sbiofit(model,gData,responseMap,estimatedParams,dose,... 'ErrorModel','combined');
Use Weights Instead of an Error Model
You can specify weights as a numeric matrix, where the number of columns corresponds to the number of responses. Setting all weights to 1 is equivalent to the constant error model.
weightsNumeric = ones(size(gData.Conc));
fitWeightsNumeric = sbiofit(model,gData,responseMap,estimatedParams,dose,'Weights',weightsNumeric);Alternatively, you can use a function handle that accepts a vector of predicted response values and returns a vector of weights. In this example, use a function handle that is equivalent to the proportional error model.
weightsFunction = @(y) 1./y.^2;
fitWeightsFunction = sbiofit(model,gData,responseMap,estimatedParams,dose,'Weights',weightsFunction);Compare Information Criteria for Model Selection
Compare the loglikelihood, AIC, and BIC values of each model to see which error model best fits the data. A larger likelihood value indicates the corresponding model fits the model better. For AIC and BIC, the smaller values are better.
allResults = [fitConst,fitWeightsNumeric,fitWeightsFunction,fitProp,fitExp,fitComb];
errorModelNames = {'constant error model','equal weights','proportional weights', ...
'proportional error model','exponential error model',...
'combined error model'};
LogLikelihood = [allResults.LogLikelihood]';
AIC = [allResults.AIC]';
BIC = [allResults.BIC]';
t = table(LogLikelihood,AIC,BIC);
t.Properties.RowNames = errorModelNames;
tt=6×3 table
LogLikelihood AIC BIC
_____________ _______ _______
constant error model 3.9866 -3.9732 -2.8433
equal weights 3.9866 -3.9732 -2.8433
proportional weights -3.8472 11.694 12.824
proportional error model -3.8257 11.651 12.781
exponential error model 1.1984 1.6032 2.7331
combined error model 3.9163 -3.8326 -2.7027
Based on the information criteria, the constant error model (or equal weights) fits the data best since it has the largest loglikelihood value and the smallest AIC and BIC.
Display Estimated Parameter Values
Show the estimated parameter values of each model.
Estimated_Central = zeros(6,1); Estimated_Cl_Central = zeros(6,1); t2 = table(Estimated_Central,Estimated_Cl_Central); t2.Properties.RowNames = errorModelNames; for i = 1:height(t2) t2{i,1} = allResults(i).ParameterEstimates.Estimate(1); t2{i,2} = allResults(i).ParameterEstimates.Estimate(2); end t2
t2=6×2 table
Estimated_Central Estimated_Cl_Central
_________________ ____________________
constant error model 1.6993 0.53358
equal weights 1.6993 0.53358
proportional weights 1.9045 0.51734
proportional error model 1.8777 0.51147
exponential error model 1.7872 0.51701
combined error model 1.7008 0.53271
Conclusion
This example showed how to estimate PK parameters, namely the volume of the central compartment and clearance parameter of an individual, by fitting the PK profile data to one-compartment model. You compared the information criteria of each model and estimated parameter values of different error models to see which model best explained the data. Final fitted results suggested both the constant and combined error models provided the closest estimates to the parameter values used to generate the data. However, the constant error model is a better model as indicated by the loglikelihood, AIC, and BIC information criteria.
Version History
Introduced in R2014a
See Also
LeastSquaresResults object | NLINResults object | sbiofit | sbiofitmixed
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)