Access the tf Transformation Tree in ROS
The tf system in ROS keeps track of multiple coordinate frames and maintains the relationship between them in a tree structure. tf is distributed, so that all coordinate frame information is available to every node in the ROS network. MATLAB® enables you to access this transformation tree. This example familiarizes you with accessing the available coordinate frames, retrieving transformations between them, and transform points, vectors, and other entities between any two coordinate frames.
Prerequisites: Get Started with ROS, Connect to a ROS Network
Start up
Initialize the ROS system.
rosinit
To create a realistic environment for this example, use exampleHelperROSStartTfPublisher to broadcast several transformations. The transformations represent a camera that is mounted on a robot.
There are three coordinate frames that are defined in this transformation tree:
the robot base frame (
robot_base)the camera's mounting point (
mounting_point)the optical center of the camera (
camera_center)
Two transforms are being published:
the transformation from the robot base to the camera's mounting point
the transformation from the mounting point to the center of the camera
exampleHelperROSStartTfPublisher
A visual representation of the three coordinate frames looks as follows.
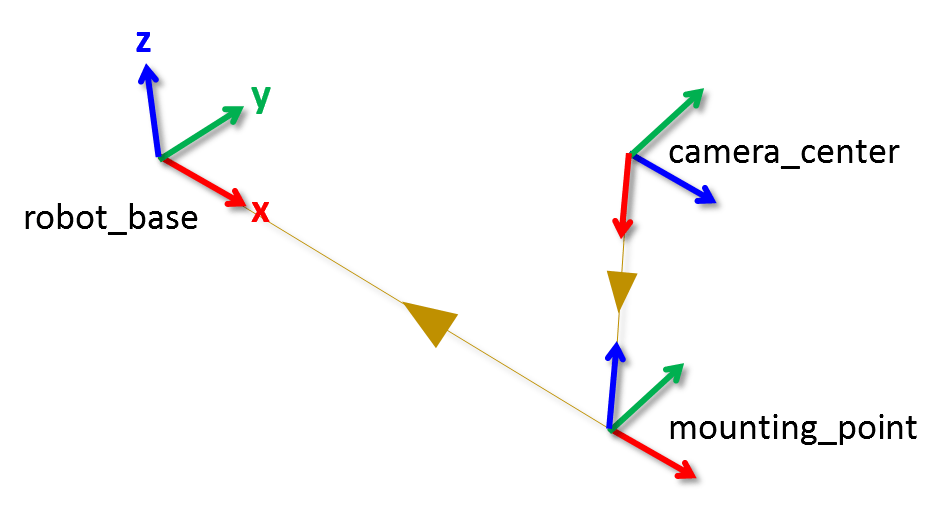
Here, the x, y, and z axes of each frame are represented by red, green, and blue lines respectively. The parent-child relationship between the coordinate frames is shown through a brown arrow pointing from the child to its parent frame.
Create a new transformation tree object with the rostf function. You can use this object to access all available transformations and apply them to different entities.
tftree = rostf
tftree =
TransformationTree with properties:
AvailableFrames: {0×1 cell}
LastUpdateTime: [0×1 Time]
BufferTime: 10
Once the object is created, it starts receiving tf transformations and buffers them internally. Keep the tftree variable in the workspace so that it continues to receive data.
Pause for a little bit to make sure that all transformations are received.
pause(2);
You can see the names of all the available coordinate frames by accessing the AvailableFrames property.
tftree.AvailableFrames
ans = 3×1 cell
{'camera_center' }
{'mounting_point'}
{'robot_base' }
This should show the three coordinate frames that describe the relationship between the camera, its mounting point, and the robot.
Receive Transformations
Now that the transformations are available, you can inspect them. Any transformation is described by a ROS geometry_msgs/TransformStamped message and has a translational and rotational component.
Retrieve the transformation that describes the relationship between the mounting point and the camera center. Use the getTransform function to do that.
mountToCamera = getTransform(tftree, 'mounting_point', 'camera_center'); mountToCameraTranslation = mountToCamera.Transform.Translation
mountToCameraTranslation =
ROS Vector3 message with properties:
MessageType: 'geometry_msgs/Vector3'
X: 0
Y: 0
Z: 0.5000
Use showdetails to show the contents of the message
quat = mountToCamera.Transform.Rotation
quat =
ROS Quaternion message with properties:
MessageType: 'geometry_msgs/Quaternion'
X: 0
Y: 0.7071
Z: 0
W: 0.7071
Use showdetails to show the contents of the message
mountToCameraRotationAngles = rad2deg(quat2eul([quat.W quat.X quat.Y quat.Z]))
mountToCameraRotationAngles = 1×3
0 90 0
Relative to the mounting point, the camera center is located 0.5 meters along the z-axis and is rotated by 90 degrees around the y-axis.
To inspect the relationship between the robot base and the camera's mounting point, call getTransform again.
baseToMount = getTransform(tftree, 'robot_base', 'mounting_point'); baseToMountTranslation = baseToMount.Transform.Translation
baseToMountTranslation =
ROS Vector3 message with properties:
MessageType: 'geometry_msgs/Vector3'
X: 1
Y: 0
Z: 0
Use showdetails to show the contents of the message
baseToMountRotation = baseToMount.Transform.Rotation
baseToMountRotation =
ROS Quaternion message with properties:
MessageType: 'geometry_msgs/Quaternion'
X: 0
Y: 0
Z: 0
W: 1
Use showdetails to show the contents of the message
The mounting point is located at 1 meter along the robot base's x-axis.
Apply Transformations
Assume now that you have a 3D point that is defined in the camera_center coordinate frame and you want to calculate what the point coordinates in the robot_base frame are.
Use the waitForTransform function to wait until the transformation between the camera_center and robot_base coordinate frames becomes available. This call blocks until the transform that takes data from camera_center to robot_base is valid and available in the transformation tree.
waitForTransform(tftree, 'robot_base', 'camera_center');
Now define a point at position [3 1.5 0.2] in the camera center's coordinate frame. You will subsequently transform this point into robot_base coordinates.
pt = rosmessage('geometry_msgs/PointStamped'); pt.Header.FrameId = 'camera_center'; pt.Point.X = 3; pt.Point.Y = 1.5; pt.Point.Z = 0.2;
You can transform the point coordinates by calling the transform function on the transformation tree object. Specify what the target coordinate frame of this transformation is. In this example, use robot_base.
tfpt = transform(tftree, 'robot_base', pt)tfpt =
ROS PointStamped message with properties:
MessageType: 'geometry_msgs/PointStamped'
Header: [1×1 Header]
Point: [1×1 Point]
Use showdetails to show the contents of the message
The transformed point tfpt has the following 3D coordinates.
tfpt.Point
ans =
ROS Point message with properties:
MessageType: 'geometry_msgs/Point'
X: 1.2000
Y: 1.5000
Z: -2.5000
Use showdetails to show the contents of the message
Besides PointStamped messages, the transform function allows you to transform other entities like poses (geometry_msgs/PoseStamped), quaternions (geometry_msgs/QuaternionStamped), and point clouds (sensor_msgs/PointCloud2).
If you want to store a transformation, you can retrieve it with the getTransform function.
robotToCamera = getTransform(tftree, 'robot_base', 'camera_center')
robotToCamera =
ROS TransformStamped message with properties:
MessageType: 'geometry_msgs/TransformStamped'
Header: [1×1 Header]
ChildFrameId: 'camera_center'
Transform: [1×1 Transform]
Use showdetails to show the contents of the message
This transformation can be used to transform coordinates in the camera_center frame into coordinates in the robot_base frame.
robotToCamera.Transform.Translation
ans =
ROS Vector3 message with properties:
MessageType: 'geometry_msgs/Vector3'
X: 1
Y: 0
Z: 0.5000
Use showdetails to show the contents of the message
robotToCamera.Transform.Rotation
ans =
ROS Quaternion message with properties:
MessageType: 'geometry_msgs/Quaternion'
X: 0
Y: 0.7071
Z: 0
W: 0.7071
Use showdetails to show the contents of the message
Send Transformations
You can also broadcast a new transformation to the ROS network.
Assume that you have a simple transformation that describes the offset of the wheel coordinate frame relative to the robot_base coordinate frame. The wheel is mounted -0.2 meters along the y-axis and -0.3 along the z-axis. The wheel has a relative rotation of 30 degrees around the y-axis.
Create the corresponding geometry_msgs/TransformStamped message that describes this transformation. The source coordinate frame, wheel, is placed to the ChildFrameId property. The target coordinate frame, robot_base, is added to the Header.FrameId property.
tfStampedMsg = rosmessage('geometry_msgs/TransformStamped'); tfStampedMsg.ChildFrameId = 'wheel'; tfStampedMsg.Header.FrameId = 'robot_base';
The transformation itself is described in the Transform property. It contains a Translation and a Rotation. Fill in the values that are listed above.
The Rotation is described as a quaternion. To convert the 30 degree rotation around the y-axis to a quaternion, you can use the axang2quat (Navigation Toolbox) function. The y-axis is described by the [0 1 0] vector and 30 degrees can be converted to radians with the deg2rad function.
tfStampedMsg.Transform.Translation.X = 0; tfStampedMsg.Transform.Translation.Y = -0.2; tfStampedMsg.Transform.Translation.Z = -0.3; quatrot = axang2quat([0 1 0 deg2rad(30)])
quatrot = 1×4
0.9659 0 0.2588 0
tfStampedMsg.Transform.Rotation.W = quatrot(1); tfStampedMsg.Transform.Rotation.X = quatrot(2); tfStampedMsg.Transform.Rotation.Y = quatrot(3); tfStampedMsg.Transform.Rotation.Z = quatrot(4);
Use rostime to retrieve the current system time and use that to timestamp the transformation. This lets the recipients know at which point in time this transformation was valid.
tfStampedMsg.Header.Stamp = rostime('now');Use the sendTransform function to broadcast this transformation.
sendTransform(tftree, tfStampedMsg)
The new wheel coordinate frame is now also in the list of available coordinate frames.
tftree.AvailableFrames
ans = 4×1 cell
{'camera_center' }
{'mounting_point'}
{'robot_base' }
{'wheel' }
The final visual representation of all four coordinate frames looks as follows.

You can see that the wheel coordinate frame has the translation and rotation that you specified in sending the transformation.
Stop Example Publisher and Shut Down ROS Network
Stop the example transformation publisher.
exampleHelperROSStopTfPublisher
Shut down the ROS master and delete the global node.
rosshutdown