wcdiskmarginplot
Syntax
Description
wcdiskmarginplot( plots the nominal and
worst-case disk-based gain and phase margins for the SISO or MIMO negative feedback loop
Lunc)feedback(Lunc,eye(N)), where N is the number of
inputs and outputs in the uncertain open-loop response Lunc.

For MIMO responses, diskmarginplot uses multiloop disk margins.
(For details about disk-based gain and phase margins, see diskmargin.)
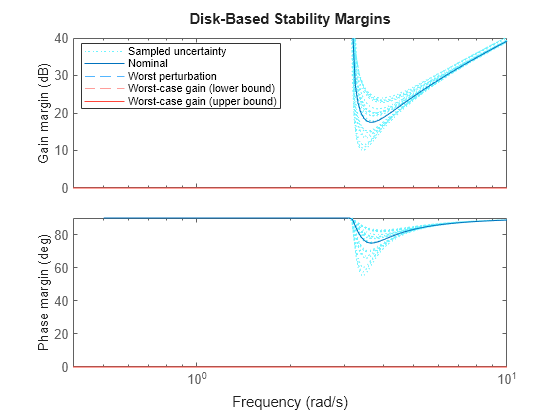
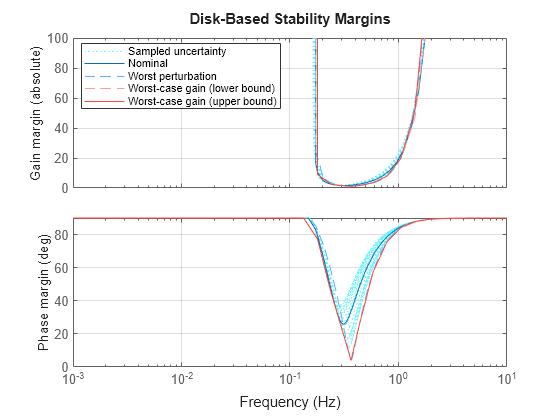
The plot includes:
Nominal — Nominal gain and phase margins of
Lunc. The disk-based gain margin at each frequency is ±GM, where GM is the value shown in the plot in dB. Similarly, the disk-based phase margin is ±PM degrees, where PM is the value shown on the plot.Worst perturbation — The disk-based gain and phase margins for the worst perturbation within the uncertainty range
Lunc.Uncertainty. The worst perturbation corresponds to thewcuoutput argument ofwcdiskmargin. It is the perturbation that yields the smallest disk margin.Worst-case margin (lower bound) — Lower bound on the worst-case margins at each frequency. This curve represents the envelope produced by finding the smallest disk margin possible at each frequency, within the uncertainty of
Lunc.Worst-case margin (upper bound) — Upper bound on the worst-case margins at each frequency.
Sampled Uncertainty — Margins of responses randomly sampled from
Lunc.
wcdiskmarginplot(
plots the disk-based gain and phase margins computed using the skew
Lunc,sigma)sigma to bias the gain variation toward gain increase
(sigma > 0) or gain decrease (sigma < 0). If
you have used wc to obtain worst-case disk-based margins with some
particular sigma, you can use this syntax to see the frequency
dependence of the margins at that sigma value. For
sigma ≠ 0, the plotted value is GM =
min(gmax,1/max(0,gmin)). In other words, the plot shows the largest amount of
gain change [1/GM,GM] that fits within the disk-based gain margin
[gmin,gmax] of the system at the specified sigma.
wcdiskmarginplot(___, plots the
worst-case margins at the frequencies specified by w)w.
If
wis a cell array of the form{wmin,wmax}, then the plot shows the margins at frequencies ranging betweenwminandwmax.If
wis a vector of frequencies, then the plot shows the margins at each specified frequency.
wcdiskmarginplot(___, uses
specified options to customize plot elements, aspects of the worst-case margin computation,
or both. Use opts)diskmarginoptions to specify customizations for the plot.
Use wcOptions to specify customizations for the computation. You can
use this argument with any of the previous syntaxes.
Examples
Input Arguments
Version History
Introduced in R2020a
See Also
diskmarginplot | diskmargin | diskmarginoptions | wcdiskmargin | wcOptions