actual2normalized
Transform actual values to normalized values
Syntax
NV = actual2normalized(uElement,AV)
[NV,ndist]
= actual2normalized(uElement,AV)
Description
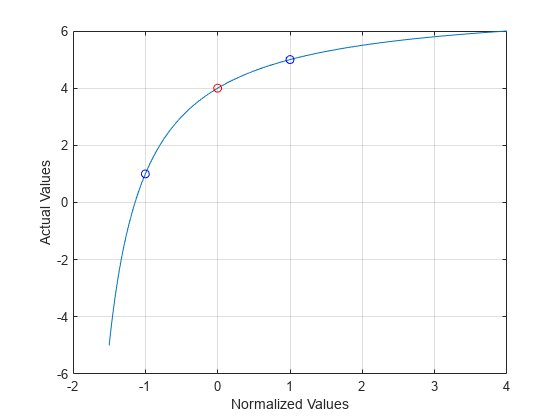
NV = actual2normalized(uElement,AV)AV of the uncertain element uElement into normalized values NV. If AV is the nominal value of uElement, NV is 0. Otherwise, AV values inside the uncertainty range of uElement map to the unit ball ||NV|| <= 1, and values outside the uncertainty range map to ||NV|| > 1. The argument AV can contain a single value or an array of values. NV has the same dimensions as AV.
[ also returns the normalized distance NV,ndist]
= actual2normalized(uElement,AV)ndist between the values AV and the nominal value of uElement. This distance is the norm of NV. Therefore, ndist <= 1 for values inside the uncertainty range of uElement, and ndist > 1 for values outside the range. If AV is an array of values, then ndist is an array of normalized distances.
The robustness margins computed byrobstab and robgain serve as bounds for the normalized distances in ndist. For example, if an uncertain system has a stability margin of 1.4, this system is stable for all uncertain element values whose normalized distance from the nominal is less than 1.4.
Examples
Algorithms
For details on the normalize distance, see Normalizing Functions for Uncertain Elements.
Version History
Introduced before R2006a
See Also
normalized2actual | robstab | robgain | getLimits | uscale