sdhinfnorm
Compute L2 norm of continuous-time system in feedback with discrete-time system
Syntax
[gaml,gamu] = sdhinfnorm(sdsys,k) [gaml,gamu] = sdhinfnorm(sdsys,k,delay) [gaml,gamu] = sdhinfnorm(sdsys,k,delay,tol)
Description
[gaml,gamu] = sdhinfnorm(sdsys,k) computes the L2 induced norm of a continuous-time LTI plant, sdsys, in feedback with a discrete-time controller, k, connected through an ideal sampler and a zero-order hold (see figure below). sdsys must be strictly proper, such that the constant feedback gain must be zero. The outputs, gamu and gaml, are upper and lower bounds on the induced L2 norm of the sampled-data closed-loop system.
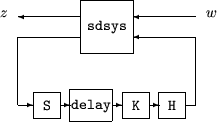
[gaml,gamu] = sdhinfnorm(sdsys,k,h,delay) includes the input argument delay. delay is a nonnegative integer associated with the number of computational delays of the controller. The default value of the delay is 0.
[gaml,gamu] = sdhinfnorm(sdsys,k,h,delay,tol) includes the input argument, tol, which defines the difference between upper and lower bounds when search terminates. The default value of tol is 0.001.
Examples
Consider an open-loop, continuous-time transfer function p = 30/s(s+30) and a continuous-time controller k = 4/(s+4). The closed-loop continuous-time system has a peak magnitude across frequency of 1.
p = ss(tf(30,[1 30])*tf([1],[1 0]));
k = ss(tf(4,[1 4]));
cl = feedback(p,k);
norm(cl,'inf')
ans =
1
Initially the controller is to be implemented at a sample rate of 1.5 Hz. The sample-data norm of the closed-loop system with the discrete-time controller is 1.0.
kd = c2d(k,0.75,'zoh');
[gu,gl] = sdhinfnorm([1; 1]*p*[1 1],-kd);
[gu gl]
ans =
3.7908 3.7929
Because of the large difference in norm between the continuous-time and sampled-data closed-loop system, the sample rate of the controller is increased from 1.5 Hz to 5 Hz. The sample-data norm of the new closed-loop system is 3.79.
kd = c2d(k,0.2,'zoh');
[gu,gl] = sdhinfnorm([1; 1]*p*[1 1],-kd);
[gu gl]
ans =
1.0044 1.0049
Algorithms
sdhinfnorm uses variations of the formulas described in the Bamieh and Pearson paper to obtain an equivalent discrete-time system. (These variations are done to improve the numerical conditioning of the algorithms.) A preliminary step is to determine whether the norm of the continuous-time system over one sampling period without control is less than the given value. This requires a search and is, computationally, a relatively expensive step.
References
Bamieh, B.A., and J.B. Pearson, “A General Framework for Linear Periodic Systems with Applications to Sampled-Data Control,” IEEE Transactions on Automatic Control, Vol. AC–37, 1992, pp. 418-435.
Version History
Introduced before R2006a
