mixsyn
Mixed-sensitivity H∞ synthesis method for robust control loop-shaping design
Syntax
Description
[
computes a controller that minimizes the H∞
norm of the weighted closed-loop transfer function K,CL,gamma,info] = mixsyn(G,W1,W2,W3)
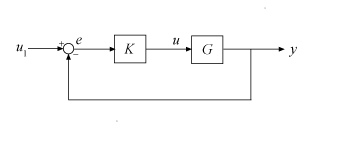
where S = (I + GK)–1 and T = (I – S) is the complementary sensitivity of the following control system.
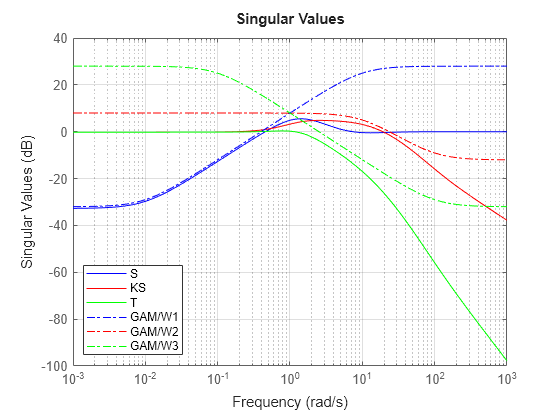
You choose the weighting functions W1,W2,W3 to shape the frequency
responses for tracking and disturbance rejection, controller effort, and noise reduction and
robustness, respectively. For details about how to choose weighting functions, see Mixed-Sensitivity Loop Shaping.
mixsyn computes the controller K that yields
the minimum ||M(s)||∞, which is
returned as gamma. For the returned controller
K,
[
calculates a controller for the target performance level K,CL,gamma] = mixsyn(G,W1,W2,W3,gamTry)gamTry.
Specifying gamTry can be useful when the optimal controller performance
is better than you need for your application. In that case, a less-than-optimal controller
can have smaller gains and be better conditioned numerically. When
W1,W2,W3 capture the desired limits on the gains of
S, KS, and T, use
gamtry = 1 to just enforce those limits.
If gamTry is not achievable, mixsyn returns
[] for K and CL, and
Inf for gamma.
[
searches the range K,CL,gamma] = mixsyn(G,W1,W2,W3,gamRange)gamRange for the best achievable performance.
Specify the range with a vector of the form [gmin,gmax]. Limiting the
search range can speed up computation by reducing the number of iterations performed by
mixsyn to test different performance levels.
[
specifies additional computation options. To create K,CL,gamma] = mixsyn(___,opts)opts, use hinfsynOptions.
Specify opts after all other input arguments.
Examples
Input Arguments
Output Arguments
Algorithms
mixsyn uses your weighting functions to generate an augmented plant
P = augw(G,W1,W2,W3). It then invokes hinfsyn to
find a controller that minimizes the H∞ norm of the
closed-loop transfer function M(s) =
LFT(P,K). For details, see Mixed-Sensitivity Loop Shaping.