Simulate a Maritime Radar PPI
This example shows how to simulate a plan position indicator (PPI) radar image for a rotating antenna array in a maritime environment. You will configure a radar scenario and spectral sea surface model, emulate a cargo ship with a cuboid extended target, generate return signals, and plot a PPI image of the result.
Configure the Radar Scenario
Set the RNG seed for repeatable results.
rng defaultThe scenario will consist of a large rotating uniform linear array (ULA) mounted in a fixed position above a sea surface. A large cuboid target will be placed on the sea surface.
Define the radar system parameters. Use an X-band radar at 10 GHz with a 1 degree azimuth beamwidth and 14 meter range resolution.
freq = 10e9; % Hz azbw = 1; % deg rngres = 14; % m
Calculate the number of uniformly-spaced elements required to achieve the desired beamwidth, and create a phased.ULA. Set the BackBaffled property of the array element to true so that only returns from the pointing direction are included.
sinc3db = 0.8859; numelems = round(2*sinc3db/deg2rad(azbw)); lambda = freq2wavelen(freq); array = phased.ULA(numelems,lambda/2); array.Element.BackBaffled = true;
Let the radar rotate at 50 rpm and express this in deg/sec. Calculate the rotation period from this rate.
rotrate = 50/60*360; % deg/sec rotperiod = 360/rotrate; % sec
Calculate the whole number of pulses required to minimally cover 360 degrees with the specified azimuth beamwidth. Use the rotation period to find the required pulse repetition frequency (PRF).
npulses = ceil(360/azbw);
prf = npulses/rotperiod; % HzThe fast-time sampling rate must be a whole multiple of the PRF. Use the desired range resolution to find the required sampling rate then adjust to match this constraint with the PRF. The radar will use a short pulse with one sample per resolution cell.
sampleRate = 1/range2time(rngres); % Hz sampleRate = prf*round(sampleRate/prf); rngres = time2range(1/sampleRate); % m sampleTime = 1/sampleRate; % s
Now create the radarTransceiver, and set the required parameters. Assume the radar is 24 meters above sea level. Returns will only be considered from a minimum ground range of 200 meters out to the maximum ground range of the sea surface. The sea surface will be defined on a square region of size 2 km-by-2 km.
% Radar height and ground range limits rdrHeight = 24; % Radar height (m) seaLength = 2e3; % Sea surface length (m) minGndRng = 200; % Minimum ground range (m) maxGndRng = seaLength/2; % Maximum ground range (m) % Slant range limits minRange = sqrt(minGndRng^2 + rdrHeight^2); % Minimum slant range (m) maxRange = sqrt(maxGndRng^2 + rdrHeight^2); % Maximum slant range (m) % Radar transceiver rdr = radarTransceiver('RangeLimits',[minRange maxRange]); rdr.TransmitAntenna.OperatingFrequency = freq; rdr.ReceiveAntenna.OperatingFrequency = freq; rdr.TransmitAntenna.Sensor = array; rdr.ReceiveAntenna.Sensor = array; rdr.Waveform.PRF = prf; rdr.Receiver.SampleRate = sampleRate; rdr.Waveform.SampleRate = sampleRate; rdr.Waveform.PulseWidth = 1/sampleRate;
Create a radarScenario and set the UpdateRate to 0 to let the update rate be derived from the radarTransceiver configuration.
scenario = radarScenario('UpdateRate',0);Now configure the sea surface. The seaSpectrum object is used to define the spectral model for the surface. The Resolution property defines the spacing of the underlying grid in the spatial domain. The resolution must be a factor of the length of the surface, so specify a desired surface resolution of 1/4th of the radar's range resolution, which is sufficient to capture the shape of the waves.
seaRes = rngres/4; % m seaRes = seaLength/round(seaLength/seaRes); spec = seaSpectrum('Resolution',seaRes);
The surfaceReflectivitySea object is used to specify the reflectivity model that will be associated with the surface. Use the NRL reflectivity model with a sea state of 5. Assume horizontal polarization.
refl = surfaceReflectivitySea('Model','NRL','SeaState',5,'Polarization','H');
Create the 2 km-by-2 km sea surface using the reflectivity and spectral models. Specify the wind speed as 10 m/s and the wind direction as 0 degrees so the wind is blowing in the +X direction.
windSpeed = 10; % m/s windDir = 0; % deg bdry = [-1 1;-1 1]*seaLength/2; % m seaSurface(scenario,'Boundary',bdry,'RadarReflectivity',refl,'SpectralModel',spec,'WindSpeed',windSpeed,'WindDirection',windDir);
Create the radar platform. Use the kinematicTrajectory object to mount the radar 24 meters above sea level, and use the AngularVelocity parameter to specify the rotation rate about the Z axis in radians per second.
traj = kinematicTrajectory('Position',[0 0 rdrHeight],'AngularVelocitySource','Property','AngularVelocity',[0 0 deg2rad(rotrate)]); platform(scenario,'Sensors',rdr,'Trajectory',traj);
Now define the cuboid target. Specify the target dimensions, total RCS, position, heading, and speed.
tgtdims = struct('Length',120,'Width',18,'Height',22,'OriginOffset',[0 0 0]); % m tgtrcs = 40; % dBsm tgtpos = [seaLength/3 seaLength/16 5]; tgthdg = -30; % deg tgtspd = 8; % m/s
Form the target velocity vector, create a kinematic trajectory, and add the target platform to the scene.
tgtvel = tgtspd*[cosd(tgthdg) sind(tgthdg) 0]; tgttraj = kinematicTrajectory('Position',tgtpos,'Velocity',tgtvel,'Orientation',rotz(tgthdg).'); platform(scenario,'Trajectory',tgttraj,'Signatures',rcsSignature('Pattern',tgtrcs),'Dimensions',tgtdims);
Finally, enable clutter generation for the radar by calling the clutterGenerator method on the scenario. The 3 dB beamwidth of the beam is used for clutter generation by default. In order to capture more of the surface return, disable this by setting UseBeam to false, and instead use a RingClutterRegion with an azimuth coverage 16 times that of the beam to encompass some sidelobes. Set the clutter resolution to half the range resolution. The azimuth center can be 0 to indicate that the region is centered about the +X direction. The ringClutterRegion method returns a handle to this region so that the parameters can be modified during the simulation.
clut = clutterGenerator(scenario,rdr,'UseBeam',false,'Resolution',rngres/2); azCov = 16*azbw; azCen = 0; reg = ringClutterRegion(clut,minGndRng,maxGndRng,azCov,azCen);
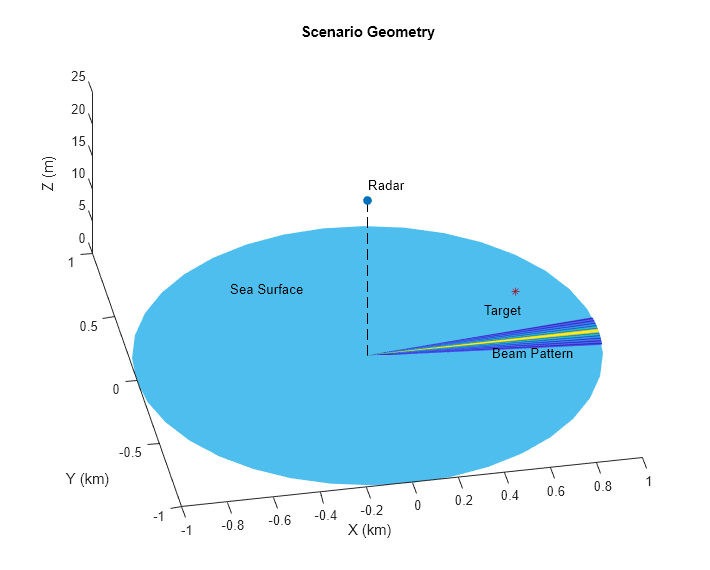
Use the provided helper function to create a visualization of the scenario.
helperPlotScenarioGeometry(rdrHeight,seaLength,array,freq,tgtpos)
Run the Simulation and Collect Returns
Each frame of the simulation will generate a range profile for one azimuth pointing direction. After receiving the raw IQ data on each frame, a phased.RangeResponse object will be used to perform matched filtering. Create the response object now, specifying the sample rate used, and get the required matched filter coefficients from the radar's waveform object.
resp = phased.RangeResponse('RangeMethod','Matched filter','SampleRate',sampleRate); mfc = getMatchedFilter(rdr.Waveform);
Specify how much of the full 360 degrees you would like to simulate. The scan starts at 0 degrees azimuth, and 20 degrees of coverage is enough to see the target.
azcov =  20;
20;Set the scenario stop time based on the desired azimuth coverage.
scenario.StopTime = azcov/360*npulses/prf;
Run the simulation. Keep track of the frame number of each loop, and get the vector of range bins from the range response object. The matrix ppi will contain the signal data formatted as range-by-azimuth. Trim the data to the ranges of interest. Use the min and max ground range defined earlier, and then find the range gate indices that correspond to those ranges.
frame = 0; nrng = floor(time2range(1/prf)/rngres); rngbins = [0 time2range((1:(nrng-1))*sampleTime)].'; minGate = max(find(rngbins >= minRange,1,'first') - 1,1); maxGate = min(find(rngbins <= maxRange,1,'last') + 2,numel(rngbins)); rngbins = rngbins(minGate:maxGate); nrng = numel(rngbins); nframes = scenario.StopTime*prf + 1; ppi = zeros(nrng,nframes); while advance(scenario) % Advance frame frame = frame + 1; reg.AzimuthCenter = (frame-1)*rotrate/prf; % Collect IQ data iqsig = receive(scenario); % Pulse compress and add to PPI ppi(:,frame) = resp(sum(iqsig{1},2),mfc); end
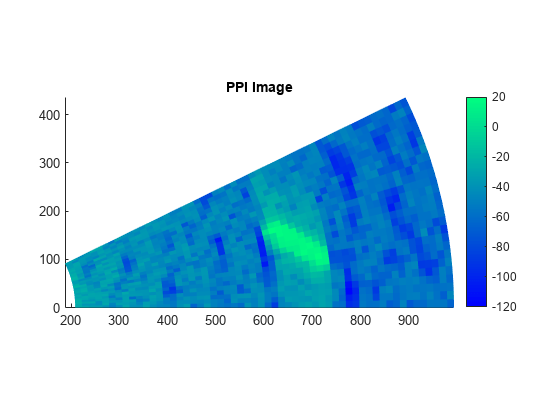
Create a PPI Image
A PPI image consists of a set of range profiles arranged in radial lines to form a circular image of the scene in Cartesian space.
Convert the azimuth pointing angles and range bins to rectangular coordinates, and then use the surface function to plot the image. When specifying the azimuth domain for the image, use one more point than the number of pulses so that the image fully encompasses all azimuth angles.
az = rotrate*(0:frame)/prf; gndrng = sqrt(rngbins.^2-rdrHeight^2); x = gndrng.*cosd(az); y = gndrng.*sind(az); figure() surface(x,y,zeros(size(x)),mag2db(abs(ppi))) shading flat view(0,90) colorbar clim([-120 20]) axis equal axis tight colormap winter title('PPI Image')
The gif below shows an example recording of this scenario over about 24 seconds.
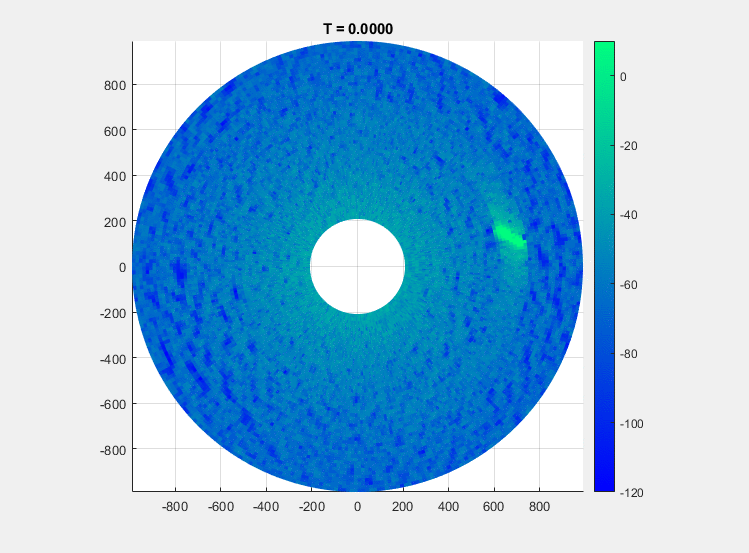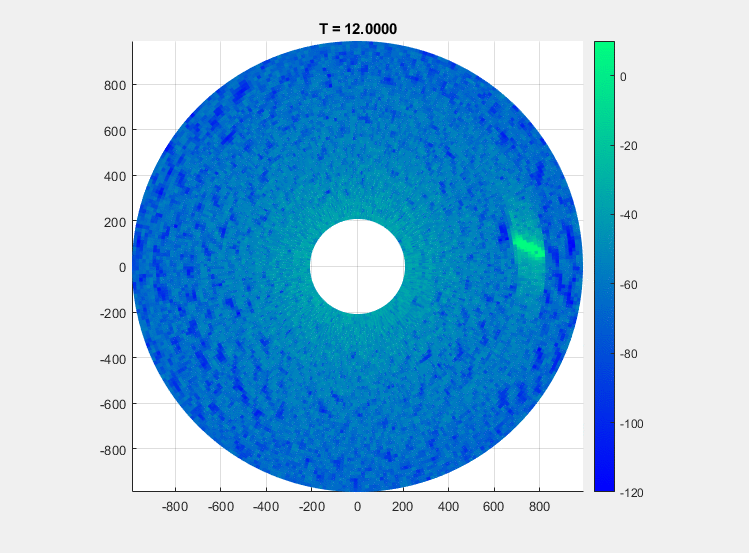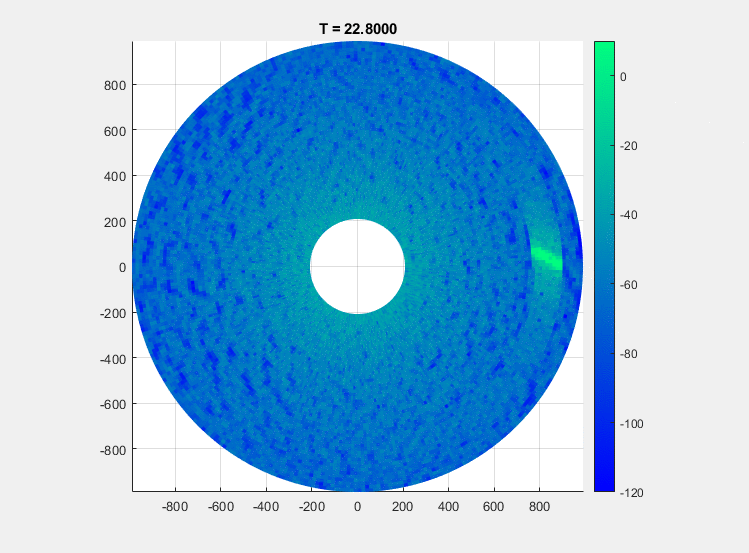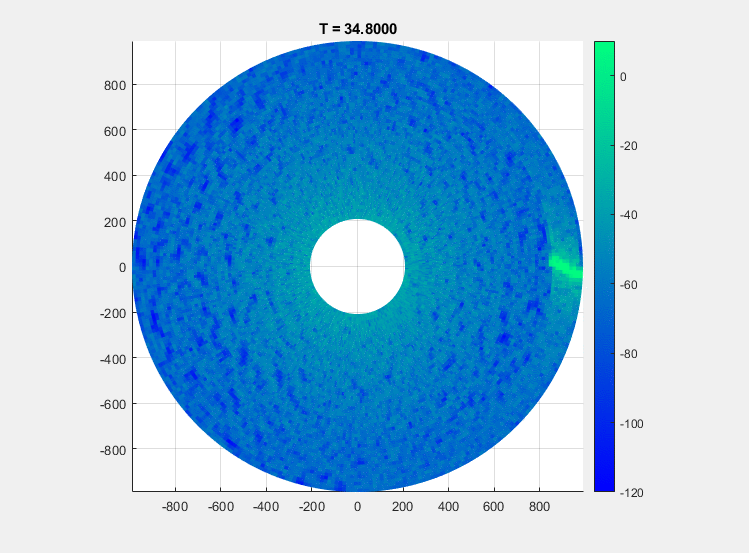
Conclusion
In this example, you saw how to generate clutter and target returns with a rotating radar in a maritime environment. You saw how to use a spectral model to get realistic sea heights and surface shadowing, and how to emulate an extended target, which allows for partial occlusion of the target by the surface. The IQ data was converted from polar format to Cartesian and plotted the surface function to create a simple PPI image.
Supporting Functions
helperPlotScenarioGeometry
function helperPlotScenarioGeometry(rdrHeight,seaLength,array,freq,tgtpos) % Plot a visualization of the scenario fh = figure; % Surface t = 0:10:360; r = linspace(0,seaLength/2,10).'; x = r.*cosd(t); y = r.*sind(t); co = colororder; surface(x/1e3,y/1e3,zeros(size(x)),repmat(permute(co(6,:),[1 3 2]),[size(x) 1]),'EdgeColor','flat') hold on % Antenna pattern az = linspace(-6,6,80); maxEl = -atand(2*rdrHeight/seaLength); el = linspace(-90,maxEl,80); G = pattern(array,freq,az,el); [az,el] = meshgrid(az,el); [x,y,~] = sph2cart(az*pi/180,el*pi/180,1); rtg = rdrHeight./sind(-el); surface(x.*rtg/1e3,y.*rtg/1e3,1e-2*ones(size(x)),G,'EdgeColor','flat') % Radar line(0,0,rdrHeight,'Color',co(1,:),'Marker','o','MarkerFaceColor',co(1,:)) line([0 0],[0 0],[0 rdrHeight],'Color','black','linestyle','--') % Target line(tgtpos(1)/1e3,tgtpos(2)/1e3,tgtpos(3),'Marker','*','Color',co(7,:)) hold off % Add text text(0,0,rdrHeight*1.1,'Radar') text(tgtpos(1)*.8/1e3,tgtpos(2)*1.1/1e3,rdrHeight/10,'Target') text(seaLength/4/1e3,-200/1e3,rdrHeight/10,'Beam Pattern') text(-seaLength/4/1e3,seaLength/4/1e3,rdrHeight/10,'Sea Surface') % Add labels xlabel('X (km)') ylabel('Y (km)') zlabel('Z (m)') title('Scenario Geometry') % Set color limits cl = clim; clim([cl(2)-30 cl(2)]) fh.Position = fh.Position + [0 0 150 150]; view([-11 58]) pause(0.5) end