Fault Diagnosis of Centrifugal Pumps Using Steady State Experiments
This example shows a model based approach for detection and diagnosis of different types of faults that occur in a pumping system. The example follows the centrifugal pump analysis presented in the Fault Diagnosis Applications book by Rolf Isermann [1].
Pump Supervision and Fault Detection
Pumps are essential equipment in many industries including power and chemical, mineral and mining, manufacturing, heating, air conditioning and cooling. Centrifugal pumps are used to transport fluids by the conversion of rotational kinetic energy to the hydrodynamic energy of the fluid flow. The rotational energy typically comes from a combustion engine or electric motor. The fluid enters the pump impeller along or near to the rotating axis and is accelerated by the impeller, flowing radially outward into a diffuser.
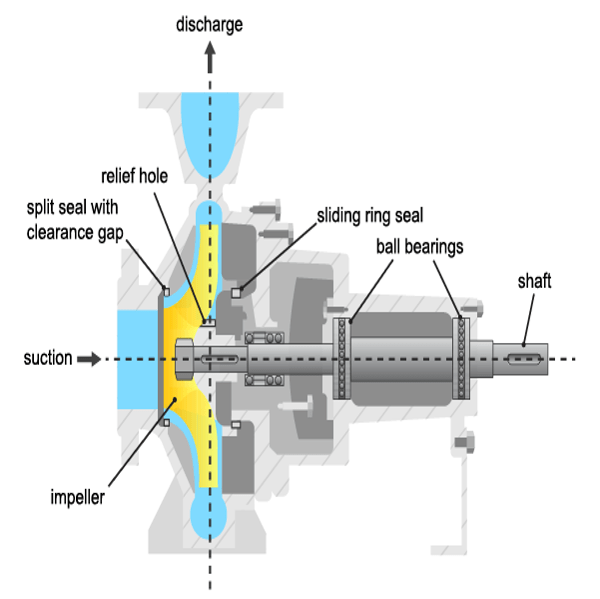
Pumps experience damage to their hydraulic or mechanical components. The most frequently faulting components are the sliding ring seals and the ball bearings, although failures to other components including the driving motor, impeller blades and sliding bearings are also not uncommon. The table below lists the most common types of faults.
Cavitation: Development of vapor bubbles inside the fluid if static pressure falls below vapor pressure. Bubbles collapse abruptly leading to damage at the blade wheels.
Gas in fluid: A pressure drop leads to dissolved gas in the fluid. A separation of gas and liquid and lower head results.
Dry Run: Missing fluid leads to lack of cooling and overheating of bearing. Important for starting phase.
Erosion: Mechanical damage to the walls because of hard particles or cavitation
Corrosion: Damage by aggressive fluids
Bearing wear: Mechanical damage through fatigue and metal friction, generation of pitting and tears
Plugging of relief bore holes: Leads to overloading/damage of axial bearings
Plugging of sliding ring seals: Leads to higher friction and smaller efficiency
Increase of split seals: Leads to loss of efficiency
Deposits: Deposits of organic material or through chemical reactions at the rotor entrance or outlet reduce efficiency and increase temperature.
Oscillations: Rotor imbalance through damage or deposits at the rotor. Can cause bearing damage.
Available Sensors
The following signals are typically measured:
Pressure difference between the inlet and outlet
Rotational speed
Motor torque and pump torque
Fluid discharge (flow) rate at the pump outlet
Driving motor current, voltage, temperature (not considered here)
Fluid temperature, sediments (not considered here)
Mathematical Models of Pump and Pipe System
A torqueapplied to the rotor of a radial centrifugal pump leads to a rotational speed and transmits a momentum increase of the pump fluid from the rotor inlet of a smaller radius to the rotor outlet of a larger radius. Euler's turbine equations yields the relationship between the pressure differential , speed and fluid discharge rate (flow rate) :
where is the theoretical (ideal; without losses) pump head measured in meters and , are proportionality constants. When accounting for a finite number of impeller blades, friction losses and impact losses due to non-tangential flow, the real pump head is given by:
where , and are proportionality constants to be treated as model parameters. The corresponding pump torque is:
The mechanical parts of the motor and the pump cause the speed to increase when torque is applied according to:
where is the ratio of inertia of the motor and the pump, and is the frictional torque consisting of Coulomb friction and viscous friction according to:
The pump is connected to a piping system that transports the fluid from a lower storage tank to an upper one. The momentum balance equation yields:
where is a resistance coefficient of the pipe, with pipe length and cross-sectional area , and is the height of the storage over the pump. The model parameters are either known from physics or can be estimated by fitting the measured sensor signals to the inputs/outputs of the model. The type of the model used may depend upon the operating conditions under which the pump is run. For example, full nonlinear model of the pump-pipe system may not be required if the pump is always run at a constant angular speed.
Fault Detection Techniques
Faults can be detected by examining certain features extracted from the measurements and comparing them to known thresholds of acceptable behavior. The detectability and isolability of different faults depends upon the nature of the experiment and availability of measurements. For example, a constant-speed analysis with pressure measurements only can detect faults causing large pressure changes. Furthermore, it cannot reliably assess the cause of the failure. However, a multi-speed experiment with measurements of pressure differential, motor torque and flow rate can detect and isolate many sources of faults such as those originating from gas enclosures, dry run, large deposits, motor defects etc.
A model based approach employs the following techniques:
Parameter estimation: Using the measurements from the healthy (nominal) operation of the machine, the parameters of the model are estimated and their uncertainty is quantified. The test system measurements are then used to re-estimate the parameter values and the resulting estimates are compared against their nominal values. This technique is the main topic of this example.
Residue generation: A model is trained as before for a healthy machine. The output of the model is compared against the measured observations from a test system and a residual signal is computed. This signal is analyzed for its magnitude, variance and other properties to detect faults. A large number of residues may be designed and employed to distinguish different sources of faults. This technique is discussed in the Fault Diagnosis of Centrifugal Pumps using Residual Analysis example.
Constant Speed Experimentation: Fault Analysis by Parameter Estimation
A common practice for pump calibration and supervision is to run it at a constant speed and record the pump's static head and fluid discharge rate. By changing the valve position in the piping system, the fluid discharge volume (GPM) is regulated. An increase in discharge rate causes the pump head to decrease. The pump's measured head characteristics can be compared against the manufacturer-supplied values. Any differences would indicate possibility of faults. The measurements for delivery head and flow discharge rate were obtained by simulations of a pump-pipe system model in Simulink.
At a nominal speed of 2900 RPM, the ideal pump head characteristics for a healthy pump supplied by the manufacturer are as shown.
url = 'https://www.mathworks.com/supportfiles/predmaint/fault-diagnosis-of-centrifugal-pumps-using-steady-state-experiments/PumpCharacteristicsData.mat'; websave('PumpCharacteristicsData.mat',url); load PumpCharacteristicsData Q0 H0 M0 % manufacturer supplied data for pump's delivery head figure plot(Q0, H0, '--'); xlabel('Discharge Rate Q (m^3/h)') ylabel('Pump Head (m)') title('Pump Delivery Head Characteristics at 2900 RPM') grid on legend('Healthy pump')
The faults that cause a discernible change in pump characteristics are:
Wear at the clearance gap
Wear at the impeller outlet
Deposits at the impeller outlet
For analyzing the faulty pumps, the speed, torque and flow rate measurements were collected for pumps affected by different faults. For example when the fault introduced is in the clearance ring, the measured head characteristics for pumps show a clear shift in the characteristic curve.
load PumpCharacteristicsData Q1 H1 M1 % signals measured for a pump with a large clearance gap hold on plot(Q1, H1); load PumpCharacteristicsData Q2 H2 M2 % signals measured for a pump with a small clearance gap plot(Q2, H2); legend('Healthy pump','Large clearance','Small clearance') hold off

Similar changes can be seen in torque-flow characteristics and for other fault types.
For automation of fault diagnosis, you turn the observed changes to quantitative information. A reliable way to do so is to fit a parameterized curve to the head-flow characteristic data plotted above. Using the pump-pipe dynamics governing equations, and using a simplified torque relationship, the following equations are obtained:
are the parameters to be estimated. If you measure and , the parameter can be estimated by linear least squares. These parameters are the features that can be used to develop a fault detection and diagnosis algorithm.
Preliminary Analysis: Comparing Parameter Values
Compute and plot the parameter values estimated for the above 3 curves. Use the measured values of and as data and as the nominal pump speed.
w = 2900; % RPM % Healthy pump [hnn_0, hnv_0, hvv_0, k0_0, k1_0, k2_0] = linearFit(0, {w, Q0, H0, M0}); % Pump with large clearance [hnn_1, hnv_1, hvv_1, k0_1, k1_1, k2_1] = linearFit(0, {w, Q1, H1, M1}); % Pump with small clearance [hnn_2, hnv_2, hvv_2, k0_2, k1_2, k2_2] = linearFit(0, {w, Q2, H2, M2}); X = [hnn_0 hnn_1 hnn_2; hnv_0 hnv_1 hnv_2; hvv_0 hvv_1 hvv_2]'; disp(array2table(X,'VariableNames',{'hnn','hnv','hvv'},... 'RowNames',{'Healthy','Large Clearance', 'Small Clearance'}))
hnn hnv hvv
__________ __________ _________
Healthy 5.1164e-06 8.6148e-05 0.010421
Large Clearance 4.849e-06 8.362e-05 0.011082
Small Clearance 5.3677e-06 8.4764e-05 0.0094656
Y = [k0_0 k0_1 k0_2; k1_0 k1_1 k1_2; k2_0 k2_1 k2_2]'; disp(array2table(Y,'VariableNames',{'k0','k1','k2'},... 'RowNames',{'Healthy','Large Clearance', 'Small Clearance'}))
k0 k1 k2
__________ ________ __________
Healthy 0.00033347 0.016535 2.8212e-07
Large Clearance 0.00031571 0.016471 3.0285e-07
Small Clearance 0.00034604 0.015886 2.6669e-07
The tables show that and values reduce when clearance gap is large while they are larger than nominal values for small clearance. On the other hand, and values increase for large clearance gap and decrease for small gap. The dependence of and on clearance gap is less clear.
Incorporating Uncertainty
The preliminary analysis showed how parameter changes can indicate fault. However, even for healthy pumps there are variations in measurements owing to the measurement noise, fluid contamination and viscosity changes and the slip-torque characteristics of the motor running the pump. These measurement variations introduce uncertainty in the parameter estimates.
Collect 5 sets of measurements from a pump operating under no-fault condition by running it at 2900 RPM for 10 discharge throttle valve positions.
url = 'https://www.mathworks.com/supportfiles/predmaint/fault-diagnosis-of-centrifugal-pumps-using-steady-state-experiments/FaultDiagnosisData.mat'; websave('FaultDiagnosisData.mat',url); load FaultDiagnosisData HealthyEnsemble H = cellfun(@(x)x.Head,HealthyEnsemble,'uni',0); Q = cellfun(@(x)x.Discharge,HealthyEnsemble,'uni',0); plot(cat(2,Q{:}),cat(2,H{:}),'k.') title('Pump Head Characteristics Ensemble for 5 Test Runs') xlabel('Flow rate (m^3/hed)') ylabel('Pump head (m)')

The plot shows variation in characteristics even for a healthy pump under realistic conditions. These variations have to be taken into consideration for making the fault diagnosis reliable. The next sections discuss fault detection and isolation techniques for noisy data.
Anomaly Detection
In many situations, the measurements of only the healthy machines are available. In that case, a statistical description of the healthy state, encapsulated by mean value and covariance of the parameter vector, can be created using available measurements. The measurements of the test pump can be compared against the nominal statistics to test whether it is plausible that the test pump is a healthy pump. A faulty pump is expected to detected as an anomaly in a view of detection features.
Estimate mean and covariance of pump head and torque parameters.
load FaultDiagnosisData HealthyEnsemble [HealthyTheta1, HealthyTheta2] = linearFit(1, HealthyEnsemble); meanTheta1 = mean(HealthyTheta1,1); meanTheta2 = mean(HealthyTheta2,1); covTheta1 = cov(HealthyTheta1); covTheta2 = cov(HealthyTheta2);
Visualize the parameter uncertainty as 74% confidence regions, which corresponds to 2 standard deviations (). See helper function helperPlotConfidenceEllipsoid for details.
% Confidence ellipsoid for pump head parameters f = figure; f.Position(3) = f.Position(3)*2; subplot(121) helperPlotConfidenceEllipsoid(meanTheta1,covTheta1,2,0.6); xlabel('hnn') ylabel('hnv') zlabel('hvv') title('2-sd Confidence Ellipsoid for Pump Head Parameters') hold on
% Confidence ellipsoid for pump torque parameters subplot(122) helperPlotConfidenceEllipsoid(meanTheta2,covTheta2,2,0.6); xlabel('k0') ylabel('k1') zlabel('k2') title('2-sd Confidence Ellipsoid for Pump Torque Parameters') hold on
The grey ellipsoids show confidence regions of healthy pump parameters. Load unlabeled test data for comparison against the healthy region.
load FaultDiagnosisData TestEnsemble
TestEnsemble contains a set of pump speed, torque, head and flow rate measurements at various valve positions. All measurements contain clearance gap fault of different magnitudes.
% Test data preview disp(TestEnsemble{1}(1:5,:)) % first 5 measurement rows from the first ensemble member
Time Run ValvePosition Speed Head Discharge Torque
_________ ___ _____________ ______ ______ _________ _______
180 sec 1 10 3034.6 12.367 35.339 0.35288
180.1 sec 1 10 2922.1 9.6762 36.556 4.6953
180.2 sec 1 10 2636.1 11.168 36.835 9.8898
180.3 sec 1 10 2717.4 10.562 40.22 -12.598
180.4 sec 1 10 3183.7 10.55 40.553 14.672
Compute test parameters. See helper function linearFit.
% TestTheta1: pump head parameters % TestTheta2: pump torque parameters [TestTheta1,TestTheta2] = linearFit(1, TestEnsemble); subplot(121) plot3(TestTheta1(:,1),TestTheta1(:,2),TestTheta1(:,3),'g*') view([-42.7 10]) subplot(122) plot3(TestTheta2(:,1),TestTheta2(:,2),TestTheta2(:,3),'g*') view([-28.3 18])

Each green star marker is contributed by one test pump. The markers that are outside the confidence bounds can be treated as outliers while those inside are either from a healthy pump or escaped detection. Note that a marker from a particular pump may be marked as anomalous in the pump head view but not in the pump torque view. This could be owing to different sources of faults being detected by these views, or the underlying reliability of pressure and torque measurements.
Quantifying Anomaly Detection Using Confidence Regions
In this section a way of utilizing the confidence region information for detection and assessing severity of faults is discussed. The technique is to compute the "distance" of a test sample from the mean or median of the healthy region distribution. The distance must be relative to the normal "spread" of the healthy parameter data represented by its covariance. The function MAHAL computes the Mahalanobis distance of test samples from the distribution of a reference sample set (the healthy pump parameter set here):
ParDist1 = mahal(TestTheta1, HealthyTheta1); % for pump head parametersIf you assume 74% confidence bound (2 standard deviations) as acceptable variation for healthy data, any values in ParDist1 that are greater than 2^2 = 4 should be tagged as anomalous and hence indicative of faulty behavior.
Add the distance values to the plot. The red lines mark the anomalous test samples. See helper function helperAddDistanceLines.
Threshold = 2; disp(table((1:length(ParDist1))',ParDist1, ParDist1>Threshold^2,... 'VariableNames',{'PumpNumber','SampleDistance','Anomalous'}))
PumpNumber SampleDistance Anomalous
__________ ______________ _________
1 58.874 true
2 24.051 true
3 6.281 true
4 3.7179 false
5 13.58 true
6 3.0723 false
7 2.0958 false
8 4.7127 true
9 26.829 true
10 0.74682 false
helperAddDistanceLines(1, ParDist1, meanTheta1, TestTheta1, Threshold);
Similarly for pump torque:
ParDist2 = mahal(TestTheta2, HealthyTheta2); % for pump torque parameters disp(table((1:length(ParDist2))',ParDist2, ParDist2>Threshold^2,... 'VariableNames',{'PumpNumber','SampleDistance','Anomalous'}))
PumpNumber SampleDistance Anomalous
__________ ______________ _________
1 9.1381 true
2 5.4249 true
3 3.0565 false
4 3.775 false
5 0.77961 false
6 7.5508 true
7 3.3368 false
8 0.74834 false
9 3.6478 false
10 1.0241 false
helperAddDistanceLines(2, ParDist2, meanTheta2, TestTheta2, Threshold); view([8.1 17.2])

The plots now not only show detection of the anomalous samples but also quantify their severity.
Quantifying Anomaly Detection Using One-Class Classifier
Another effective technique to flag anomalies is to build a one-class classifier for the healthy parameter dataset. Train an SVM classifier using the healthy pump parameter data. Since there are no fault labels utilized, treat all samples as coming from the same (healthy) class. Since changes in parameters and are most indicative of potential faults, use only these parameters for training the SVM classifier.
nc = size(HealthyTheta1,1); rng(2) % for reproducibility SVMOneClass1 = fitcsvm(HealthyTheta1(:,[1 3]),ones(nc,1),... 'KernelScale','auto',... 'Standardize',true,... 'OutlierFraction',0.0455);
Plot the test observations and the decision boundary. Flag the support vectors and potential outliers. See helper function helperPlotSVM.
figure helperPlotSVM(SVMOneClass1,TestTheta1(:,[1 3])) title('SVM Anomaly Detection for Pump Head Parameters') xlabel('hnn') ylabel('hvv')

The boundary separating the outliers from the rest of the data occurs where the contour value is 0; this is the level curve marked with "0" in the plot. The outliers are marked with red circles. A similar analysis can be performed for torque parameters.
SVMOneClass2 = fitcsvm(HealthyTheta2(:,[1 3]),ones(nc,1),... 'KernelScale','auto',... 'Standardize',true,... 'OutlierFraction',0.0455); figure helperPlotSVM(SVMOneClass2,TestTheta2(:,[1 3])) title('SVM Anomaly Detection for Torque Parameters') xlabel('k0') ylabel('k2')

A similar analysis can be carried out for detecting other kinds of faults such as wear or deposits at impeller outlet as discussed next in the context of fault isolation.
Fault Isolation Using Steady-State Parameters as Features
If the information on the type of fault(s) in the test system is available, it can be used to create algorithms that not only detect faults but also indicate their type.
A. Distinguishing Clearance Gap Faults by Likelihood Ratio Tests
Changes in clearance gap can be split into two types - smaller than expected gap (yellow line in the pump head characteristic plot) and larger than expected gap (red line). Load pump test data sets containing clearance gap faults where the nature of fault (large or small) is known in advance. Use these fault labels to perform 3-way classification among the following modes:
Mode 1: Normal clearance gap (healthy behavior)
Mode 2: Large clearance gap
Mode 3: Small clearance gap
url = 'https://www.mathworks.com/supportfiles/predmaint/fault-diagnosis-of-centrifugal-pumps-using-steady-state-experiments/LabeledGapClearanceData.mat'; websave('LabeledGapClearanceData.mat',url); load LabeledGapClearanceData HealthyEnsemble LargeGapEnsemble SmallGapEnsemble
The ensembles contain data from 50 independent experiments. Fit steady-state linear models as before to parameterize the pump head and torque data.
[HealthyTheta1, HealthyTheta2] = linearFit(1,HealthyEnsemble); [LargeTheta1, LargeTheta2] = linearFit(1,LargeGapEnsemble); [SmallTheta1, SmallTheta2] = linearFit(1,SmallGapEnsemble);
Plot the parameter histograms to check if there is separability among the 3 modes. The function histfit is used to plot the histograms and the corresponding fitted normal distribution curves. See helper function helperPlotHistogram.
Pump head parameters:
helperPlotHistogram(HealthyTheta1, LargeTheta1, SmallTheta1, {'hnn','hnv','hvv'})
The histogram shows that offers good separability among the three modes but parameters have overlapping probability distribution functions (PDFs).
Pump torque parameters:
helperPlotHistogram(HealthyTheta2, LargeTheta2, SmallTheta2, {'k0','k1','k2'})
For the Torque parameters, the individual separability is not very good. There is still some variation in mean and variances that can be exploited by a trained 3-mode classifier. If the PDFs show good separation in mean or variance, you can design likelihood ratio tests to quickly assign a test dataset to the most likely mode. This is shown next for the pump head parameters.
Let:
: hypothesis that head parameters belong to the healthy pump mode
: hypothesis that head parameters belong to the pump with large clearance gap
: hypothesis that head parameters belong to the pump with small clearance gap
Consider the available parameter sets as test samples for mode prediction. Assign the predicted mode as belonging to one for which the joint PDF has the highest value (Hypothesis is selected over if ). Then plot the results comparing the true and predicted modes in a confusion matrix. Function mvnpdf is used for computing the PDF value and the functions confusionmatrix and heatmap are used for confusion matrix visualization. See helper function pumpModeLikelihoodTest.
% Pump head confusion matrix
figure
pumpModeLikelihoodTest(HealthyTheta1, LargeTheta1, SmallTheta1)
The confusion plot shows perfect separation between the three modes, which is not surprising given the clear separation among the histograms for parameters.
% Pump torque confusion matrix
pumpModeLikelihoodTest(HealthyTheta2, LargeTheta2, SmallTheta2)
The results are slightly worse for the torque parameters. Still, the success rate is quite high (97%) even though the PDFs of the three modes overlapped significantly. This is because the PDF value calculation is affected both by the location (mean) as well as the amplitude (variance).
B. Multi-Class Classification of Fault Modes Using Tree Bagging
In this section, another classification technique is discussed that is more suitable when classification among a larger number of modes is required. Consider the following fault modes of operation of the pump:
Healthy operation
Wear at clearance gap
Small deposits at impeller outlet
Deposits at impeller inlet
Abrasive wear at impeller outlet
Broken blade
Cavitation
The classification problem is harder because there are only three parameters computed and you need to distinguish among 7 modes of operation. Thus, not only you have to compare the estimated parameters for each fault mode to the healthy mode, but also to each other - both the direction (increase or reduction in value) and magnitude (10% change vs. 70% change) of the parameter change must be taken into consideration.
Here the use of TreeBagger classifier for this problem is shown. Tree Bagger is an ensemble learning technique that uses bootstrap aggregation (bagging) of features to create decision trees that classify labeled data. 50 labeled data sets are collected for the 7 modes of operation. Estimate pump head parameters for each dataset and train the classifier using a subset of the parameter estimates from each mode.
url = 'https://www.mathworks.com/supportfiles/predmaint/fault-diagnosis-of-centrifugal-pumps-using-steady-state-experiments/MultipleFaultsData.mat'; websave('MultipleFaultsData.mat',url); load MultipleFaultsData % Compute pump head parameters HealthyTheta = linearFit(1, HealthyEnsemble); Fault1Theta = linearFit(1, Fault1Ensemble); Fault2Theta = linearFit(1, Fault2Ensemble); Fault3Theta = linearFit(1, Fault3Ensemble); Fault4Theta = linearFit(1, Fault4Ensemble); Fault5Theta = linearFit(1, Fault5Ensemble); Fault6Theta = linearFit(1, Fault6Ensemble); % Generate labels for each mode of operation Label = {'Healthy','ClearanceGapWear','ImpellerOutletDeposit',... 'ImpellerInletDeposit','AbrasiveWear','BrokenBlade','Cavitation'}; VarNames = {'hnn','hnv','hvv','Condition'}; % Assemble results in a table with parameters and corresponding labels N = 50; T0 = [array2table(HealthyTheta),repmat(Label(1),[N,1])]; T0.Properties.VariableNames = VarNames; T1 = [array2table(Fault1Theta), repmat(Label(2),[N,1])]; T1.Properties.VariableNames = VarNames; T2 = [array2table(Fault2Theta), repmat(Label(3),[N,1])]; T2.Properties.VariableNames = VarNames; T3 = [array2table(Fault3Theta), repmat(Label(4),[N,1])]; T3.Properties.VariableNames = VarNames; T4 = [array2table(Fault4Theta), repmat(Label(5),[N,1])]; T4.Properties.VariableNames = VarNames; T5 = [array2table(Fault5Theta), repmat(Label(6),[N,1])]; T5.Properties.VariableNames = VarNames; T6 = [array2table(Fault6Theta), repmat(Label(7),[N,1])]; T6.Properties.VariableNames = VarNames; % Stack all data % Use 30 out of 50 datasets for model creation TrainingData = [T0(1:30,:);T1(1:30,:);T2(1:30,:);T3(1:30,:);T4(1:30,:);T5(1:30,:);T6(1:30,:)]; % Create an ensemble Mdl of 20 decision trees for predicting the % labels using the parameter values rng(3) % for reproducibility Mdl = TreeBagger(20, TrainingData, 'Condition',... 'OOBPrediction','on',... 'OOBPredictorImportance','on')
Mdl =
TreeBagger
Ensemble with 20 bagged decision trees:
Training X: [210x3]
Training Y: [210x1]
Method: classification
NumPredictors: 3
NumPredictorsToSample: 2
MinLeafSize: 1
InBagFraction: 1
SampleWithReplacement: 1
ComputeOOBPrediction: 1
ComputeOOBPredictorImportance: 1
Proximity: []
ClassNames: 'AbrasiveWear' 'BrokenBlade' 'Cavitation' 'ClearanceGapWear' 'Healthy' 'ImpellerInletDeposit' 'ImpellerOutletDeposit'
Properties, Methods
The performance of the TreeBagger model can be computed by studying its misclassification probability for out-of-bag observations as a function of number of decision trees.
% Compute out of bag error figure plot(oobError(Mdl)) xlabel('Number of trees') ylabel('Misclassification probability')

Finally, compute prediction performance of the model on test samples that were never used for growing the decision trees.
ValidationData = [T0(31:50,:);T1(31:50,:);T2(31:50,:);T3(31:50,:);T4(31:50,:);T5(31:50,:);T6(31:50,:)]; PredictedClass = predict(Mdl,ValidationData); E = zeros(1,7); % Healthy data misclassification E(1) = sum(~strcmp(PredictedClass(1:20), Label{1})); % Clearance gap fault misclassification E(2) = sum(~strcmp(PredictedClass(21:40), Label{2})); % Impeller outlet deposit fault misclassification E(3) = sum(~strcmp(PredictedClass(41:60), Label{3})); % Impeller inlet deposit fault misclassification E(4) = sum(~strcmp(PredictedClass(61:80), Label{4})); % Abrasive wear fault misclassification E(5) = sum(~strcmp(PredictedClass(81:100), Label{5})); % Broken blade fault misclassification E(6) = sum(~strcmp(PredictedClass(101:120), Label{6})); % Cavitation fault misclassification E(7) = sum(~strcmp(PredictedClass(121:140), Label{7})); figure bar(E/20*100) xticklabels(Label) set(gca,'XTickLabelRotation',45) ylabel('Misclassification (%)')

The plot shows that the abrasive wear and broken blade faults are misclassified for 30% of the validation samples. A closer look at the predicted labels shows that in the misclassified cases, the 'AbrasiveWear' and 'BrokenBlade' labels get intermixed between each other only. This suggests that the symptoms for these fault categories are not sufficiently distinguishable for this classifier.
Summary
A well designed fault diagnosis strategy can save operating costs by minimizing service downtime and component replacement costs. The strategy benefits from a good knowledge about the operating machine's dynamics which is used in combination with sensor measurements to detect and isolate different kinds of faults.
This example discussed a parametric approach for fault detection and isolation based on steady-state experiments. This approach requires careful modeling of the system dynamics and using the parameters (or transformations thereof) as features for designing fault diagnosis algorithms. The parameters were used for training anomaly detectors, performing likelihood ratio tests and for training of multi-class classifiers.
How to make use of classification techniques in real-life testing of pumps
A summary of the fault diagnosis workflow follows.
Run the test pump at its nominal speed. Turn the discharge valve to various settings to control the flow rate. For each valve position, note down the pump speed, flow rate, pressure differentials and torque.
Estimate parameters for the pump head and pump torque characteristic (steady state) equations.
If the uncertainty/noise is low and the parameter estimates are reliable, the estimated parameters can be directly compared to their nominal values. Their relative magnitudes would indicate the nature of the fault.
In a general noisy situation, use the anomaly detection techniques to first check if there is a fault present in the system at all. This can be done very quickly by comparing the estimated parameter values against the mean and covariance values obtained from a historical database of healthy pumps.
If a fault is indicated, use the fault classification techniques (such as likelihood ratio tests or output of a classifier) to isolate the most probable cause(s). The choice of classification technique would depend upon sensor data available, their reliability, the severity of the fault and availability of historical information regarding the fault modes.
For a fault diagnosis approach based on residual analysis, see the Fault Diagnosis of Centrifugal Pumps Using Residual Analysis example.
References
Isermann, Rolf, Fault-Diagnosis Applications. Model-Based Condition Monitoring: Actuators, Drives, Machinery, Plants, Sensors, and Fault-tolerant System, Edition 1, Springer-Verlag Berlin Heidelberg, 2011.
Supporting Functions
Linear fit to pump parameters.
function varargout = linearFit(Form, Data) %linearFit Linear least squares solution for Pump Head and Torque parameters. % % If Form==0, accept separate inputs and return separate outputs. For one experiment only. % If Form==1, accept an ensemble and return compact parameter vectors. For several experiments (ensemble). if Form==0 w = Data{1}; Q = Data{2}; H = Data{3}; M = Data{4}; n = length(Q); if isscalar(w), w = w*ones(n,1); end Q = Q(:); H = H(:); M = M(:); Predictor = [w.^2, w.*Q, Q.^2]; Theta1 = Predictor\H; hnn = Theta1(1); hnv = -Theta1(2); hvv = -Theta1(3); Theta2 = Predictor\M; k0 = Theta2(2); k1 = -Theta2(3); k2 = Theta2(1); varargout = {hnn, hnv, hvv, k0, k1, k2}; else H = cellfun(@(x)x.Head,Data,'uni',0); Q = cellfun(@(x)x.Discharge,Data,'uni',0); M = cellfun(@(x)x.Torque,Data,'uni',0); W = cellfun(@(x)x.Speed,Data,'uni',0); N = numel(H); Theta1 = zeros(3,N); Theta2 = zeros(3,N); for kexp = 1:N Predictor = [W{kexp}.^2, W{kexp}.*Q{kexp}, Q{kexp}.^2]; X1 = Predictor\H{kexp}; hnn = X1(1); hnv = -X1(2); hvv = -X1(3); X2 = Predictor\M{kexp}; k0 = X2(2); k1 = -X2(3); k2 = X2(1); Theta1(:,kexp) = [hnn; hnv; hvv]; Theta2(:,kexp) = [k0; k1; k2]; end varargout = {Theta1', Theta2'}; end end
Membership likelihood test.
function pumpModeLikelihoodTest(HealthyTheta, LargeTheta, SmallTheta) %pumpModeLikelihoodTest Generate predictions based on PDF values and plot confusion matrix. m1 = mean(HealthyTheta); c1 = cov(HealthyTheta); m2 = mean(LargeTheta); c2 = cov(LargeTheta); m3 = mean(SmallTheta); c3 = cov(SmallTheta); N = size(HealthyTheta,1); % True classes % 1: Healthy: group label is 1. X1t = ones(N,1); % 2: Large gap: group label is 2. X2t = 2*ones(N,1); % 3: Small gap: group label is 3. X3t = 3*ones(N,1); % Compute predicted classes as those for which the joint PDF has the maximum value. X1 = zeros(N,3); X2 = zeros(N,3); X3 = zeros(N,3); for ct = 1:N % Membership probability density for healthy parameter sample HealthySample = HealthyTheta(ct,:); x1 = mvnpdf(HealthySample, m1, c1); x2 = mvnpdf(HealthySample, m2, c2); x3 = mvnpdf(HealthySample, m3, c3); X1(ct,:) = [x1 x2 x3]; % Membership probability density for large gap pump parameter LargeSample = LargeTheta(ct,:); x1 = mvnpdf(LargeSample, m1, c1); x2 = mvnpdf(LargeSample, m2, c2); x3 = mvnpdf(LargeSample, m3, c3); X2(ct,:) = [x1 x2 x3]; % Membership probability density for small gap pump parameter SmallSample = SmallTheta(ct,:); x1 = mvnpdf(SmallSample, m1, c1); x2 = mvnpdf(SmallSample, m2, c2); x3 = mvnpdf(SmallSample, m3, c3); X3(ct,:) = [x1 x2 x3]; end [~,PredictedGroup] = max([X1;X2;X3],[],2); TrueGroup = [X1t; X2t; X3t]; C = confusionmat(TrueGroup,PredictedGroup); heatmap(C, ... 'YLabel', 'Actual condition', ... 'YDisplayLabels', {'Healthy','Large Gap','Small Gap'}, ... 'XLabel', 'Predicted condition', ... 'XDisplayLabels', {'Healthy','Large Gap','Small Gap'}, ... 'ColorbarVisible','off'); end