Nonlinear System with Cross-Coupling Between Components
This example shows how to solve a nonlinear PDE system of two equations with cross-coupling between the two components. The system is a Schnakenberg system
with the steady-state solution and . The initial conditions are a small perturbation of the steady-state solution.
Solution for First Time Span
First, create a PDE model for a system of two equations.
model = createpde(2);
Create a cubic geometry and assign it to the model.
gm = multicuboid(1,1,1); model.Geometry = gm;
Generate the mesh using the linear geometric order to save memory.
generateMesh(model,GeometricOrder="linear");Define the parameters of the system.
D1 = 0.05; D2 = 1; kappa = 100; a = 0.2; b = 0.8;
Based on these parameters, specify the PDE coefficients in the toolbox format.
d = [1;1];
c = [D1;D2];
f = @(region,state) [kappa*(a - state.u(1,:) + ...
state.u(1,:).^2.*state.u(2,:));
kappa*(b - state.u(1,:).^2.*state.u(2,:))
];
specifyCoefficients(model,m=0,d=d,c=c,a=0,f=f);Set the initial conditions. The first component is a small perturbation of the steady-state solution . The second component is the steady-state solution .
icFcn = @(region) [a + b + 10^(-3)*exp(-100*((region.x - 1/3).^2 ... + (region.y - 1/2).^2)); ... (b/(a + b)^2)*ones(size(region.x))]; setInitialConditions(model,icFcn);
Solve the system for times 0 through 2 seconds.
tlist = linspace(0,2,10); results = solvepde(model,tlist);
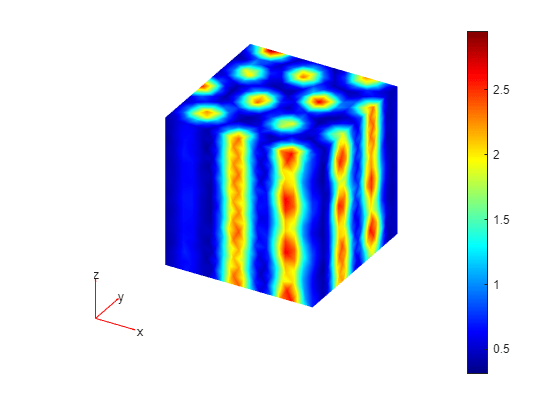
Plot the first component of the solution at the last time step.
pdeplot3D(model,ColorMapData=results.NodalSolution(:,1,end));
Initial Condition for Second Time Span Based on Previous Solution
Now, resume the analysis and solve the problem for times from 2 to 5 seconds. Reduce the magnitude of the previously obtained solution for time 2 seconds to 10% of the original value.
u2 = results.NodalSolution(:,:,end); newResults = createPDEResults(model,u2(:)*0.1);
Use newResults as the initial condition for further analysis.
setInitialConditions(model,newResults);
Solve the system for times 2 through 5 seconds.
tlist = linspace(2,5,10); results25 = solvepde(model,tlist);
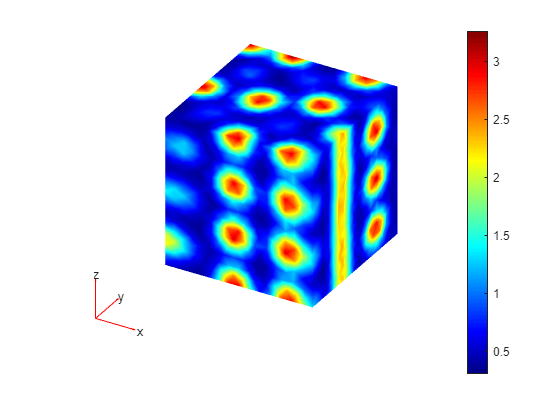
Plot the first component of the solution at the last time step.
figure pdeplot3D(model,ColorMapData=results25.NodalSolution(:,1,end));
Alternatively, you can write a function that uses the results returned by the solver and computes the initial conditions based on the results of the previous analysis.
function newU0 = computeNewIC(resultsObject) newU0 = 0.1*resultsObject.NodalSolution(:,:,end).'; end
Remove the previous initial conditions.
delete(model.InitialConditions);
Set the initial conditions using the function NewIC.
NewIC = @(location) computeNewIC(results); setInitialConditions(model,NewIC)
ans =
GeometricInitialConditions with properties:
RegionType: 'cell'
RegionID: 1
InitialValue: @(location)computeNewIC(results)
InitialDerivative: []
Solve the system for times 2 through 5 seconds.
results25f = solvepde(model,tlist);
Plot the first component of the solution at the last time step.
figure pdeplot3D(model,ColorMapData=results25f.NodalSolution(:,1,end));
