Specify Nonconstant Boundary Conditions
When solving PDEs with nonconstant boundary conditions, specify these conditions by using function handles. This example shows how to write functions to represent nonconstant boundary conditions for PDE problems.
Geometry and Mesh
Create a model.
model = createpde;
Include a unit square geometry in the model and plot the geometry.
geometryFromEdges(model,@squareg);
pdegplot(model,EdgeLabels="on")
xlim([-1.1 1.1])
ylim([-1.1 1.1])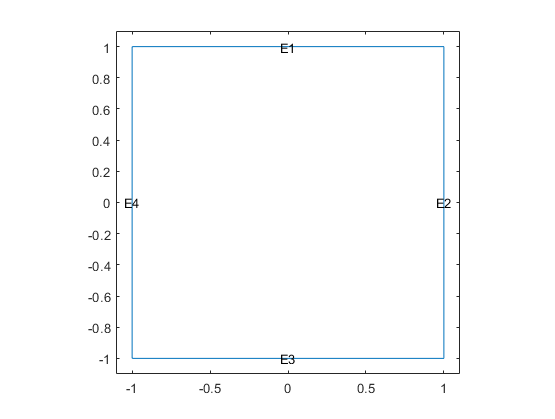
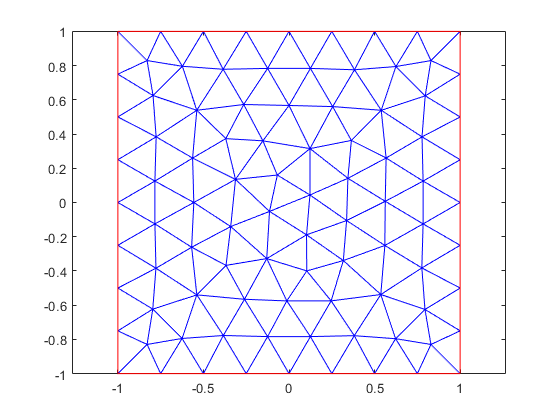
Generate a mesh with a maximum edge length of 0.25. Plot the mesh.
generateMesh(model,Hmax=0.25); figure pdemesh(model)
Scalar PDE Problem with Nonconstant Boundary Conditions
Write functions to represent the nonconstant boundary conditions on edges 1 and 3.
Each function must accept two input arguments, location and
state. The solvers automatically compute and populate the data in
the location and state structure arrays and pass
this data to your function.
Write a function that returns the value to represent the Dirichlet boundary condition for edge 1.
function bc = bcfuncD(location,state) bc = 52 + 20*location.x; scatter(location.x,location.y,"filled","black"); hold on end
Write a function that returns the value to represent the Neumann boundary condition for edge 3.
function bc = bcfuncN(location,state) bc = cos(location.x).^2; scatter(location.x,location.y,"filled","red"); hold on end
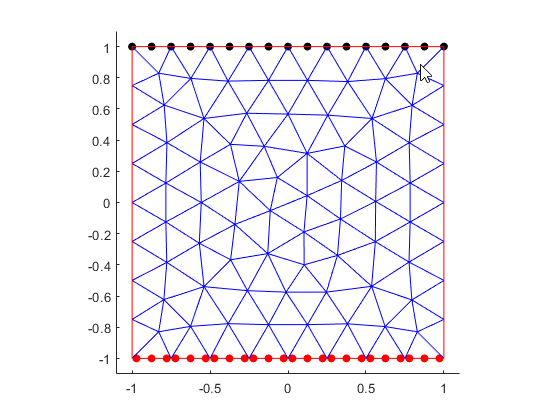
The scatter plot command in each of these functions enables you to visualize the
location data used by the toolbox. For Dirichlet boundary
conditions, the location data (black markers on edge 1) corresponds
with the mesh nodes. Each element of a quadratic mesh has nodes at its corners and edge
centers. For Neumann boundary conditions, the location data (red
markers on edge 3) corresponds with the quadrature integration points.
Specify the boundary condition for edges 1 and 3 using the functions that you wrote.
applyBoundaryCondition(model,"dirichlet", ... Edge=1,u=@bcfuncD); applyBoundaryCondition(model,"neumann", ... Edge=3,g=@bcfuncN);
Specify the PDE coefficients.
specifyCoefficients(model,m=0,d=0,c=1,a=0,f=10);
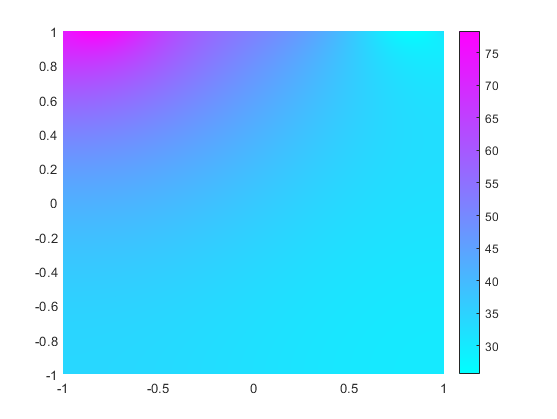
Solve the equation and plot the solution.
results = solvepde(model); figure pdeplot(model,XYData=results.NodalSolution)

Anonymous Functions for Nonconstant Boundary Conditions
If the dependency of a boundary condition on coordinates, time, or solution is simple,
you can use an anonymous function to represent the nonconstant boundary condition. Thus,
you can implement the linear interpolation shown earlier in this example as the
bcfuncD function, as this anonymous function.
bcfuncD = @(location,state)52 + 20*location.x;
Specify the boundary condition for edge 1.
applyBoundaryCondition(model,"dirichlet", ... Edge=1,u=bcfuncD);
Additional Arguments
If a function that represents a nonconstant boundary condition requires more
arguments than location and state, follow these
steps:
Write a function that takes the
locationandstatearguments and the additional arguments.Wrap that function with an anonymous function that takes only the
locationandstatearguments.
For example, define boundary conditions on edge 1 as . First, write the function that takes the arguments
a, b, and c in addition to
the location and state arguments.
function bc = bcfunc_abc(location,state,a,b,c) bc = 52*a^2 + 20*b*location.x + c; end
Because a function defining nonconstant boundary conditions must have exactly two
arguments, wrap the bcfunc_abc function with an anonymous
function.
bcfunc_add_args = @(location,state) bcfunc_abc(location,state,1,2,3);
Now you can use bcfunc_add_args to specify a boundary condition for
edge 1.
applyBoundaryCondition(model,"dirichlet", ... Edge=1,u=bcfunc_add_args);
System of PDEs
Create a model for a system of two equations.
model = createpde(2);
Use the same unit square geometry that you used for the scalar PDE problem.
geometryFromEdges(model,@squareg);
The first component on edge 1 satisfies the equation . The second component on edge 1 satisfies the equation .
Write a function file myufun.m that incorporates these
equations.
function bcMatrix = myufun(location,state) bcMatrix = [52 + 20*location.x + 10*sin(pi*(location.x.^3)); 52 - 20*location.x - 10*sin(pi*(location.x.^3))]; end
Specify the boundary condition for edge 1 using the myufun
function.
applyBoundaryCondition(model,"dirichlet",Edge=1,u=@myufun);Specify the PDE coefficients.
specifyCoefficients(model,m=0,d=0,c=1,a=0,f=[10;-10]);
Generate a mesh.
generateMesh(model);
Solve the system and plot the solution.
results = solvepde(model); u = results.NodalSolution; figure pdeplot(model,XYData=u(:,1))

figure pdeplot(model,XYData=u(:,2))