Smooth Formulations of Nonsmooth Functions
To smooth an otherwise nonsmooth problem, you can sometimes add auxiliary variables. For example,
f(x) = max(g(x),h(x))
can be a nonsmooth function even when g(x) and h(x) are smooth, as illustrated by the following functions.
f(x) is nonsmooth at the points x = π/4 and x = 5π/4.
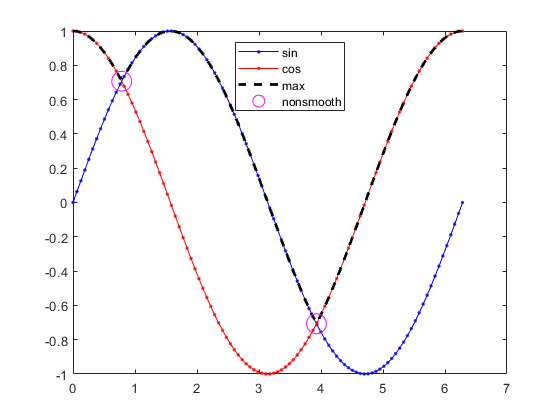
This lack of smoothness can cause problems for Optimization Toolbox™ solvers, all of which assume that objective functions and nonlinear constraint functions are continuously differentiable. So, if you try to solve
x =
mint(f(t)) starting from the point x0 = 1,
you do not get an exit flag of 1, because the solution is not differentiable at the locally minimizing point x = π/4.
fun1 = @sin; fun2 = @cos; fun = @(x)max(fun1(x),fun2(x)); [x1,fval1,eflag1] = fminunc(fun,1)
Local minimum possible.
fminunc stopped because it cannot decrease the objective function
along the current search direction.
<stopping criteria details>
x1 =
0.7854
fval1 =
0.7071
eflag1 =
5Sometimes, you can use an auxiliary variable to turn a nonsmooth problem into a smooth problem. For the previous example, consider the auxiliary variable y with the smooth constraints
Consider the optimization problem, subject to these constraints,
The resulting solution x, y is the solution to
the original problem
This formulation uses the problem-based approach.
myvar = optimvar("myvar"); auxvar = optimvar("auxvar"); smprob = optimproblem("Objective",auxvar); smprob.Constraints.cons1 = auxvar >= sin(myvar); smprob.Constraints.cons2 = auxvar >= cos(myvar); x0.myvar = 1; x0.auxvar = 1; [sol2,fval2,eflag2] = solve(smprob,x0)
Solving problem using fmincon.
Local minimum found that satisfies the constraints.
Optimization completed because the objective function is non-decreasing in
feasible directions, to within the value of the optimality tolerance,
and constraints are satisfied to within the value of the constraint tolerance.
sol2 =
struct with fields:
auxvar: 0.7071
myvar: 0.7854
fval2 =
0.7071
eflag2 =
OptimalSolutionThis same concept underlies the formulation of the fminimax
function; see Goal Attainment Method.
