Finite Difference Laplacian
This example shows how to compute and represent the finite difference Laplacian on an L-shaped domain.
Domain
The numgrid function numbers points within an L-shaped domain. The spy function is a useful tool for visualizing the pattern of nonzero elements in a matrix. Use these two functions to generate and display an L-shaped domain.
n = 32; R = 'L'; G = numgrid(R,n); spy(G) title('A Finite Difference Grid')
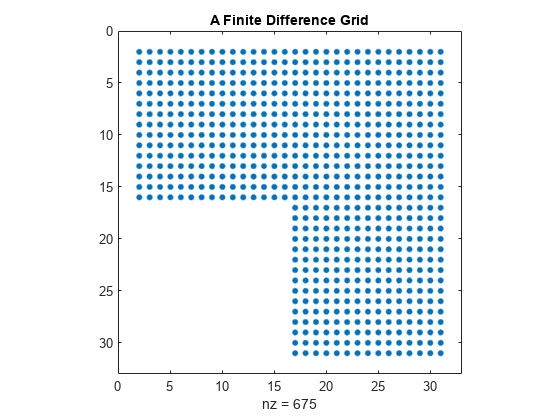
Show a smaller version of the matrix as a sample.
g = numgrid(R,10)
g = 10×10
0 0 0 0 0 0 0 0 0 0
0 1 5 9 13 17 25 33 41 0
0 2 6 10 14 18 26 34 42 0
0 3 7 11 15 19 27 35 43 0
0 4 8 12 16 20 28 36 44 0
0 0 0 0 0 21 29 37 45 0
0 0 0 0 0 22 30 38 46 0
0 0 0 0 0 23 31 39 47 0
0 0 0 0 0 24 32 40 48 0
0 0 0 0 0 0 0 0 0 0
Discrete Laplacian
Use delsq to generate the discrete Laplacian. Use the spy function again to get a graphical feel of the matrix elements.
D = delsq(G);
spy(D)
title('The 5-Point Laplacian')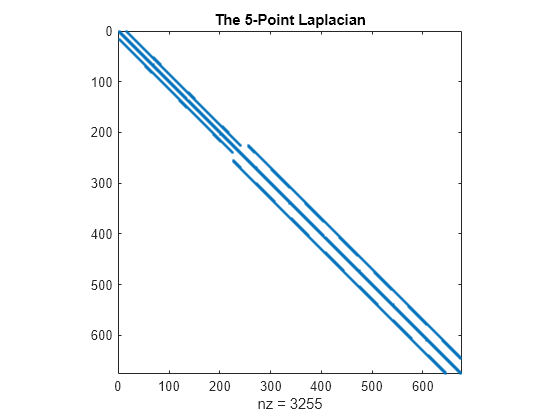
Determine the number of interior points.
N = sum(G(:)>0)
N = 675
Dirichlet Boundary Value Problem
Solve the Dirichlet boundary value problem for the sparse linear system. The problem setup is:
delsq(u) = 1 in the interior, u = 0 on the boundary.
rhs = ones(N,1); if (R == 'N') % For nested dissection, turn off minimum degree ordering. spparms('autommd',0) u = D\rhs; spparms('autommd',1) else u = D\rhs; % This is used for R=='L' as in this example end
Map the solution onto the L-shaped grid and plot it as a contour map.
U = G; U(G>0) = full(u(G(G>0))); clabel(contour(U)); prism axis square ij
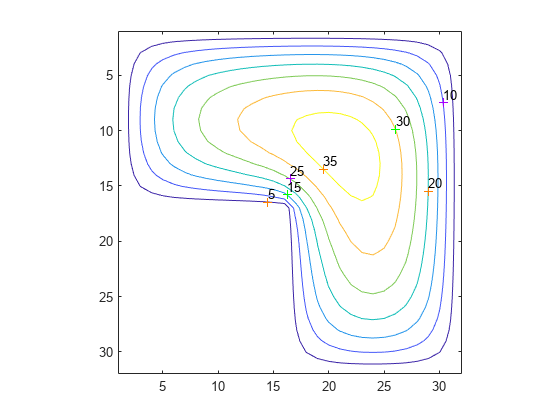
Now show the solution as a mesh plot.
mesh(U) axis([0 n 0 n 0 max(max(U))]) axis square ij
