mollweid
Mollweide Projection
Classification
Pseudocylindrical
Identifier
mollweid
Graticule
Central Meridian: Straight line half as long as the Equator.
Other Meridians: Meridians 90º east and west of the central meridian form a circle. The others are equally spaced semiellipses intersecting at the poles and concave toward the central meridian.
Parallels: Unequally spaced straight parallel lines, perpendicular to the central meridian. Spacing is greatest toward the Equator, but the spacing changes gradually.
Poles: Points.
Symmetry: About the central meridian or the Equator.
Features
This is an equal-area projection. Scale is true along the 40º44' parallels and is constant along any parallel and between any pair of parallels equidistant from the Equator. It is free of distortion only at the two points where the 40º44' parallels intersect the central meridian. This projection is not conformal or equidistant.
Parallels
For this projection, only one standard parallel is specified. The other standard parallel is the same latitude with the opposite sign. The standard parallel is by definition fixed at 40º44'.
Remarks
This projection was presented by Carl B. Mollweide in 1805. Its other names include the Homolographic, the Homalographic, the Babinet, and the Elliptical projections. It is occasionally used for thematic world maps, and it is combined with the Sinusoidal to produce the Goode Homolosine projection.
Example
landareas = shaperead('landareas.shp','UseGeoCoords',true);
axesm ('mollweid', 'Frame', 'on', 'Grid', 'on');
geoshow(landareas,'FaceColor',[1 1 .5],'EdgeColor',[.6 .6 .6]);
tissot;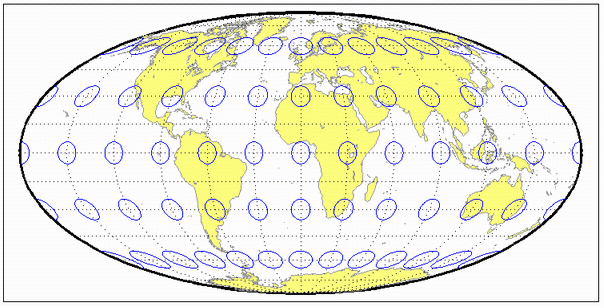
Version History
Introduced before R2006a
