Compressor (2P)
Libraries:
Simscape /
Fluids /
Two-Phase Fluid /
Fluid Machines
Description
The Compressor (2P) block represents a dynamic compressor, such as a centrifugal or axial compressor, in a two-phase fluid network. You can use the Parameterization parameter to parameterize the block analytically based on the design point or by using a tabulated compressor map. A positive rotation of port R relative to port C causes fluid to flow from port A to port B. Port R and port C are mechanical rotational conserving ports associated with the compressor shaft and casing, respectively.
The surge margin is the ratio between the surge pressure ratio and the operating point
pressure ratio along the a constant speed line, minus one. When you set
Parameterization to Tabulated, the
block outputs the surge margin at port SM.
The design point is the design operational pressure ratio across and mass flow rate through the compressor during simulation. The compressor operating point and the point of maximum efficiency do not need to coincide.
The Compressor (2P) block assumes that superheated fluid enters the inlet. You can use the Report when fluid is not fully vapor parameter to choose what the block does when the fluid does not meet superheated conditions.
Compressor Map
The compressor map plots the isentropic efficiency of the compressor and the lines of constant corrected shaft speed between the two extremes of choked flow and surge flow. To visualize the block map, right-click the block and select Fluids > Plot Compressor Map. Each time you modify the block settings, click Reload Data on the figure window.
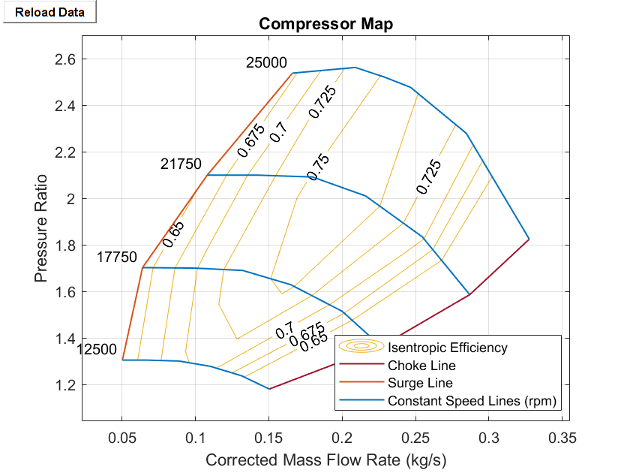
Each corrected speed line shows how the pressure ratio varies with the corrected mass flow rate when the shaft spins at the corresponding corrected speed. The variable β indicates the relative position along the corrected speed lines between the two extremes. Choked flow corresponds to β = 0 and surge flow corresponds to β = 1. The map also plots contours of isentropic efficiency as a function of pressure ratio and corrected mass flow rate, which provides a relative indication of how much power the compressor needs to operate at various combinations of pressure ratio and corrected mass flow rate.
Due to the large changes in pressure and temperature inside a compressor, the compressor map plots performance in terms of the corrected mass flow rate. The map adjusts the corrected mass flow rate from the inlet mass flow rate by using the reference pressure and reference temperature,
where:
ṁA is the mass flow rate at port A.
TA is the temperature at port A.
Tref is the value of the Reference temperature for corrected flow parameter. When you set Parameterization to
Analytical, this is the inlet temperature at the design operating condition.corr is the corrected mass flow rate. When you set Parameterization to
Analytical, the block uses the Corrected mass flow rate at design point parameter. When you set Parameterization toTabulated, the block uses the Corrected mass flow rate table, mdot(N,beta) parameter.pA is the pressure at port A.
pref is the Reference pressure for corrected flow parameter. When using the analytical parameterization, this is the inlet pressure at the design operating condition.
The block derives TA from the specific internal energy, uA, and specific pressure, pA.
The block also adjusts the shaft speed, ω, according to the reference temperature, such that the corrected shaft speed is
Shaft Torque
The block calculates the shaft torque, τ, as
where:
Δhtotal is the change in specific total enthalpy.
ηm is the compressor Mechanical efficiency.
ω is the relative shaft angular velocity, ωR - ωC.
The block relates the efficiency in the compressor map as
where:
Δhisen is the isentropic change in specific total enthalpy.
ηisen is the isentropic efficiency.
A threshold region when flow approaches zero ensures that the compressor generates no torque when the flow rate is near zero or reversed.
Analytical Parameterization
You can generate the compressor map analytically by setting
Parameterization to Analytical.
The block fits a model of the compressor map based on [1] to the specified values
for the Corrected speed at design point, Pressure
ratio at design point, and Corrected mass flow rate at
design point parameters. This method does not use
β lines and the block does not report a surge margin.
The block finds the pressure ratio at a given shaft speed and mass flow rate as
where:
πD is the Pressure ratio at design point parameter.
is the normalized corrected shaft speed,
where ND is the Corrected speed at design point parameter.
is the normalized corrected mass flow rate,
where D is the Corrected mass flow rate at design point parameter.
a is the Spine shape, a parameter.
b is the Speed line spread, b parameter.
k is the Speed line roundness, k parameter.
The spine refers to the black line where the isentropic efficiency contours start to bend. The map speed lines are the shaft constant-speed lines that intersect the spine perpendicularly.
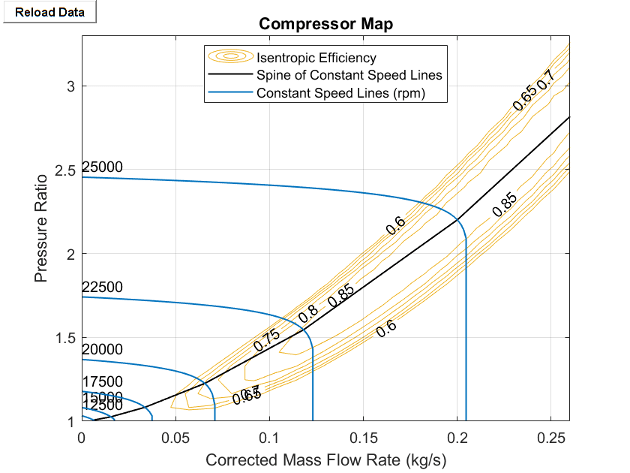
When you set Efficiency specification to
Analytical, the block models variable compressor
efficiency as
where:
η0 is the value of the Maximum isentropic efficiency parameter.
C is the value of the Efficiency contour gradient orthogonal to spine, C parameter.
D is the value of the Efficiency contour gradient along spine, D parameter.
c is the value of the Efficiency peak flatness orthogonal to spine, c parameter.
d is the value of the Efficiency peak flatness along spine, d parameter.
is the normalized corrected pressure ratio,
where πD is the Corrected pressure ratio at design point parameter.
0 is the normalized corrected mass flow rate at which the compressor reaches the value of the Maximum isentropic efficiency parameter.
You can adjust the efficiency variables for different performance characteristics. Alternatively, you can choose a constant efficiency value by using the Constant isentropic efficiency parameter.
Tabulated Data Parameterization
When you set Parameterization to
Tabulated, the isentropic efficiency, pressure ratio,
and corrected mass flow rate of the compressor are functions of the corrected speed,
N, and the map index, β. The block uses
linear interpolation between data points for the efficiency, pressure ratio, and
corrected mass flow rate.
If β exceeds 1, compressor surge occurs and the block assumes the pressure ratio remains at β = 1, while the mass flow rate continues to change. If the simulation conditions fall below β = 0, the block models the effects of choked flow, where the mass flow rate remains at its value at β = 0 while the pressure ratio continues to change. To constrain the compressor performance in the map boundaries, the block extrapolates isentropic efficiency to the nearest point.
You can choose to be notified when the operating point pressure ratio exceeds the surge
pressure ratio. Set Report when surge margin is negative to
Warning to receive a warning or to
Error to stop the simulation when this occurs.
Continuity Equations
The block conserves mass such that
where B is the mass flow rate at port B.
The block computes the energy balance equation as
where:
ΦA is the energy flow rate at port A.
ΦB is the energy flow rate at port B.
Pfluid is the hydraulic power delivered to the fluid,which the block determines from the change in specific enthalpy
Assumptions and Limitations
The block assumes that superheated fluid enters at A.
The block only defines compressor map flow from port A to port B. Reverse flow results may not be accurate.
The block only represents dynamic compressors.
Ports
Output
Conserving
Parameters
Extended Capabilities
Version History
Introduced in R2022a