Using a Complete Poll in a Generalized Pattern Search
Consider the following function.
The following figure shows a plot of the function.

 Code for generating the figure
Code for generating the figure
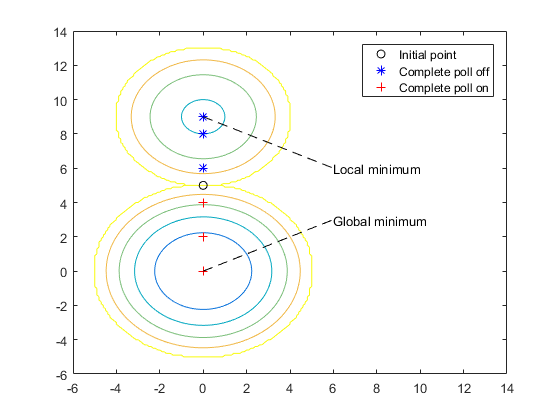
The global minimum of the function occurs at (0, 0), where its value is -25. However, the function also has a local minimum at (0, 9), where its value is -16.
To create a file that computes the function, copy and paste the following code into a new file in the MATLAB® Editor.
function z = poll_example(x) if x(1)^2 + x(2)^2 <= 25 z = x(1)^2 + x(2)^2 - 25; elseif x(1)^2 + (x(2) - 9)^2 <= 16 z = x(1)^2 + (x(2) - 9)^2 - 16; else z = 0; end end
Save the file as poll_example.m in a folder on the MATLAB path.
To run a pattern search on the function, enter the following.
options = optimoptions('patternsearch','Display','iter'); [x,fval] = patternsearch(@poll_example,[0,5],... [],[],[],[],[],[],[],options)
MATLAB returns a table of iterations and the solution.
x =
0 9
fval =
-16The algorithm begins by a=evaluating the function at the initial point, f(0, 5) = 0. The poll evaluates the following during its first iterations.
| f((0, 5) + (1, 0)) = f(1, 5) = 0 | (1) |
| f((0, 5) + (0, 1)) = f(0, 6) = -7 | (2) |
As soon as the search polls the mesh point (0, 6), at which the objective function value is less than at the initial point, it stops polling the current mesh and sets the current point at the next iteration to (0, 6). Consequently, the search moves toward the local minimum at (0, 9) at the first iteration. You see this by looking at the first two lines of the command line display.
Iter f-count f(x) MeshSize Method
0 1 0 1
1 3 -7 2 Successful PollNote that the pattern search performs only two evaluations of the objective function at the first iteration, increasing the total function count from 1 to 3.
Next, set UseCompletePoll to true and rerun the
optimization.
options.UseCompletePoll = true;
[x,fval] = patternsearch(@poll_example,[0,5],...
[],[],[],[],[],[],[],options);This time, the pattern search finds the global minimum at (0, 0). The difference
between this run and the previous one is that with UseCompletePoll
set to true, at the first iteration the pattern search polls all four
mesh points.
| f((0, 5) + (1, 0)) = f(1, 5) = 0 | (3) |
| f((0, 5) + (0, 1)) = f(0, 6) = -6 | (4) |
| f((0, 5) + (-1, 0)) = f(-1, 5) = 0 | (5) |
| f((0, 5) + (0, -1)) = f(0, 4) = -9 | (6) |
Because the last mesh point has the lowest objective function value, the pattern search selects it as the current point at the next iteration. The first two lines of the command-line display show this.
Iter f-count f(x) MeshSize Method
0 1 0 1
1 5 -9 2 Successful PollIn this case, the objective function is evaluated four times at the first iteration. As a result, the pattern search moves toward the global minimum at (0, 0).
The following figure compares the sequence of points returned when Complete
poll is set to Off with the sequence when
Complete poll is On.
 Code for generating the figure
Code for generating the figure