Cluster Quasi-Random Data Using Fuzzy C-Means Clustering
This example shows how FCM clustering works using quasi-random two-dimensional data.
Load the data set and plot it.
load fcmdata.dat plot(fcmdata(:,1),fcmdata(:,2),"o")
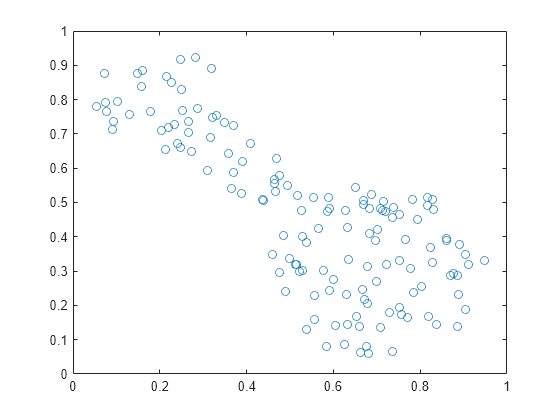
Using the fcm function, find two clusters in this data set. The clustering algorithm stops when the improvement in the objective function between subsequent iterations is below a threshold.
options = fcmOptions(NumClusters=2); [center,U,objFcn] = fcm(fcmdata,options);
Iteration count = 1, obj. fcn = 8.97048 Iteration count = 2, obj. fcn = 7.1974 Iteration count = 3, obj. fcn = 6.32558 Iteration count = 4, obj. fcn = 4.58614 Iteration count = 5, obj. fcn = 3.89311 Iteration count = 6, obj. fcn = 3.8108 Iteration count = 7, obj. fcn = 3.7998 Iteration count = 8, obj. fcn = 3.79786 Iteration count = 9, obj. fcn = 3.79751 Iteration count = 10, obj. fcn = 3.79744 Iteration count = 11, obj. fcn = 3.79743 Iteration count = 12, obj. fcn = 3.79743 Minimum improvement reached.
center contains the coordinates of the two cluster centers, U contains the membership grades for each of the data points, and objFcn contains a history of the objective function across the iterations.
To view the progress of the clustering, plot the objective function.
figure plot(objFcn) title("Objective Function Values") xlabel("Iteration Count") ylabel("Objective Function Value")

Assign each data point to the cluster for which its cluster membership is greatest.
maxU = max(U); index1 = find(U(1,:) == maxU); index2 = find(U(2,:) == maxU);
Finally, plot the clustered data along with the two cluster centers found by the fcm function. The large characters in the plot indicate the cluster centers.
figure plot(fcmdata(index1,1),fcmdata(index1,2),"og") hold on plot(fcmdata(index2,1),fcmdata(index2,2),"xr") plot(center(1,1),center(1,2),"ok",... MarkerSize=15,LineWidth=3) plot(center(2,1),center(2,2),"xk",... MarkerSize=15,LineWidth=3)

Every time you run this example, the fcm function initializes with different initial conditions. This behavior can swap the order in which the cluster centers are computed and plotted.