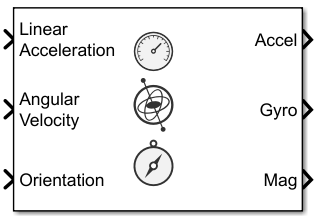
IMU
IMU simulation model
Libraries:
Sensor Fusion and Tracking Toolbox /
Multisensor Positioning /
Sensor Models
Navigation Toolbox /
Multisensor Positioning /
Sensor Models
Description
The IMU
Simulink® block models receiving data from an inertial measurement unit (IMU) composed of
accelerometer, gyroscope, and magnetometer sensors. You can specify the reference frame of the
block inputs as the NED (North-East-Down) or ENU
(East-North-Up) frame by using the Reference Frame parameter.
Examples
IMU Sensor Fusion with Simulink
Generate and fuse IMU sensor data using Simulink®. You can accurately model the behavior of an accelerometer, a gyroscope, and a magnetometer and fuse their outputs to compute orientation.
Ports
Input
Acceleration of the IMU in the local navigation coordinate system, specified as an N-by-3 matrix of real scalars in meters per second squared. N is the number of samples in the current frame. Do not include the gravitational acceleration in this input since the sensor models gravitational acceleration by default.
To specify the orientation of the IMU sensor body frame with respect to the local navigation frame, use the Orientation input port.
Data Types: single | double
Angular velocity of the IMU sensor body frame in the local navigation coordinate system, specified as an N-by-3 matrix of scalars in radians per second. N is the number of samples in the current frame. To specify the orientation of the IMU sensor body frame with respect to the local navigation frame, use the Orientation input port.
Data Types: single | double
Orientation of the IMU sensor body frame with respect to the local navigation
coordinate system, specified as an N-by-4 array of real scalars or
a 3-by-3-by-N rotation matrix. Each row the of the
N-by-4 array is assumed to be the four elements of a quaternion. N is the number of samples in the current
frame.
Data Types: single | double
Temperature of IMU, specified as an N-by-1 vector of real scalars in degrees Celsius.
Dependencies
To enable this port, in the Parameters tab, select Specify temperature from input port.
Data Types: single | double
Magnetic field vector in the local navigation coordinate system, specified as an N-by-3 matrix of scalars in microteslas.
Dependencies
To enable this port, in the Parameters tab, select Specify magnetic field from input port.
Data Types: single | double
Output
Accelerometer measurement of the IMU in the sensor body coordinate system, returned as an N-by-3 matrix of real scalars in meters per second squared. N is the number of samples in the current frame.
Data Types: single | double
Gyroscope measurement of the IMU in the sensor body coordinate system, returned as an N-by-3 matrix of real scalars in radians per second. N is the number of samples in the current frame.
Data Types: single | double
Magnetometer measurement of the IMU in the sensor body coordinate system, returned as an N-by-3 matrix of real scalars in microtesla. N is the number of samples in the current frame.
Data Types: single | double
Parameters
Parameters
Navigation reference frame, specified as NED (North-East-Down) or
ENU (East-North-Up).
Note
If you choose the NED reference frame, specify the sensor inputs in the NED reference frame. Additionally, the sensor models the gravitational acceleration as [0 0 9.81] m/s2.
If you choose the ENU reference frame, specify the sensor inputs in the ENU reference frame. Additionally, the sensor models the gravitational acceleration as [0 0 −9.81] m/s2.
Select this check box to enable the input of temperature by using the Temperature input port.
Operating temperature of the IMU in degrees Celsius, specified as a real scalar.
When the block calculates temperature scale factors and environmental drift noises, 25 oC is used as the nominal temperature.
Dependencies
To enable this parameter, clear Specify temperature from input port.
Data Types: single | double
Select this check box to enable the input of magnetic field by using the Magnetic field input port.
Magnetic field vector expressed in the NED navigation frame, specified as a 1-by-3 vector of scalars.
The default magnetic field corresponds to the magnetic field at latitude zero, longitude zero, and altitude zero.
Dependencies
To enable this parameter, set Reference frame to
NED and clear Specify magnetic field from input
port.
Data Types: single | double
Magnetic field vector expressed in the ENU navigation frame, specified as a 1-by-3 vector of scalars.
The default magnetic field corresponds to the magnetic field at latitude zero, longitude zero, and altitude zero.
Dependencies
To enable this parameter, set Reference frame to
ENU and clear Specify magnetic field from input
port.
Data Types: single | double
Initial seed of a random number generator algorithm, specified as a nonnegative integer.
Data Types: single | double
Interpreted execution— Simulate the model using the MATLAB® interpreter. This option shortens startup time. InInterpreted executionmode, you can debug the source code of the block.Code generation— Simulate the model using generated C code. The first time that you run a simulation, Simulink generates C code for the block. The C code is reused for subsequent simulations if the model does not change. This option requires additional startup time.
Accelerometer
Maximum sensor reading in m/s2, specified as a real positive scalar.
Data Types: single | double
Resolution of sensor measurements in (m/s2)/LSB, specified as a real nonnegative scalar.
Data Types: single | double
Constant sensor offset bias in m/s2, specified as a real scalar or 3-element row vector. Any scalar input is converted into a real 3-element row vector where each element has the input scalar value.
Data Types: single | double
Sensor axes skew in percentage, specified as a scalar, a 3-element row vector, or a 3-by-3 matrix. The diagonal elements of the matrix account for the misalignment effects for each axes. The off-diagonal elements account for the cross-axes misalignment effects. The measured state vmeasure is obtained from the true state vtrue via the misalignment matrix as:
If you specify the property as a scalar, then all the off-diagonal elements of the matrix take the value of the specified scalar and all the diagonal elements are 100.
If you specify the property as a vector [a b c], then m21 = m31 = a, m12 = m32 = b, and m13 = m23 = c. All the diagonal elements are 100.
Data Types: single | double
Velocity random walk in (m/s2/√Hz), specified as a real scalar or 3-element row vector. This property corresponds to the power spectral density of sensor noise. Any scalar input is converted into a real 3-element row vector where each element has the input scalar value.
Data Types: single | double
Instability of the bias offset in m/s2, specified as a real scalar or 3-element row vector. Any scalar input is converted into a real 3-element row vector where each element has the input scalar value.
Data Types: single | double
Bias instability filter numerator coefficients, specified as a real-valued row
vector. To specify coefficients for fractal noise, use the fractalcoef
function.
Data Types: single | double
Bias instability filter denominator coefficients, specified as a real-valued row
vector. To specify coefficients for fractal noise, use the fractalcoef
function.
Data Types: single | double
Acceleration random walk of sensor in (m/s2)(√Hz), specified as a real scalar or 3-element row vector. Any scalar input is converted into a real 3-element row vector where each element has the input scalar value.
Data Types: single | double
Select the type of random noise as:
double-sided— Random noise coefficients have a scale factor of 2.single-sided— Random noise coefficients have a scale factor of 1.
Data Types: single | double
Sensor bias from temperature in (m/s2)/℃, specified as a real scalar or 3-element row vector. Any scalar input is converted into a real 3-element row vector where each element has the input scalar value.
Data Types: single | double
Scale factor error from temperature in %/℃, specified as a real scalar or real 3-element row vector with values ranging from 0 to 100. Any scalar input is converted into a real 3-element row vector where each element has the input scalar value.
Data Types: single | double
Gyroscope
Maximum sensor reading in rad/s, specified as a real positive scalar.
Data Types: single | double
Resolution of sensor measurements in (rad/s)/LSB, specified as a real nonnegative scalar.
Data Types: single | double
Constant sensor offset bias in rad/s, specified as a real scalar or 3-element row vector. Any scalar input is converted into a real 3-element row vector where each element has the input scalar value.
Data Types: single | double
Sensor axes skew in percentage, specified as a scalar, a 3-element row vector, or a 3-by-3 matrix. The diagonal elements of the matrix account for the misalignment effects for each axes. The off-diagonal elements account for the cross-axes misalignment effects. The measured state vmeasure is obtained from the true state vtrue via the misalignment matrix as:
If you specify the property as a scalar, then all the off-diagonal elements of the matrix take the value of the specified scalar and all the diagonal elements are 100.
If you specify the property as a vector [a b c], then m21 = m31 = a, m12 = m32 = b, and m13 = m23 = c. All the diagonal elements are 100.
Data Types: single | double
Sensor bias from linear acceleration in (rad/s)/(m/s2), specified as a real scalar or 3-element row vector. Any scalar input is converted into a real 3-element row vector where each element has the input scalar value.
Data Types: single | double
Angle random walk of sensor in (rad/s)/(√Hz), specified as a real scalar or 3-element row vector. Any scalar input is converted into a real 3-element row vector where each element has the input scalar value.
Data Types: single | double
Instability of the bias offset in rad/s, specified as a real scalar or 3-element row vector. Any scalar input is converted into a real 3-element row vector where each element has the input scalar value.
Data Types: single | double
Bias instability filter numerator coefficients, specified as a real-valued row
vector. To specify coefficients for fractal noise, use the fractalcoef
function.
Data Types: single | double
Bias instability filter denominator coefficients, specified as a real-valued row
vector. To specify coefficients for fractal noise, use the fractalcoef
function.
Data Types: single | double
Select the type of random noise as:
double-sided— Random noise coefficients have a scale factor of 2.single-sided— Random noise coefficients have a scale factor of 1.
Data Types: single | double
Integrated white noise of sensor in (rad/s)(√Hz), specified as a real scalar or 3-element row vector. Any scalar input is converted into a real 3-element row vector where each element has the input scalar value.
Data Types: single | double
Sensor bias from temperature in (rad/s)/℃, specified as a real scalar or 3-element row vector. Any scalar input is converted into a real 3-element row vector where each element has the input scalar value.
Data Types: single | double
Scale factor error from temperature in %/℃, specified as a real scalar or real 3-element row vector with values ranging from 0 to 100. Any scalar input is converted into a real 3-element row vector where each element has the input scalar value.
Data Types: single | double
Magnetometer
Maximum sensor reading in μT, specified as a real positive scalar.
Data Types: single | double
Resolution of sensor measurements in (μT)/LSB, specified as a real nonnegative scalar.
Data Types: single | double
Constant sensor offset bias in μT, specified as a real scalar or 3-element row vector. Any scalar input is converted into a real 3-element row vector where each element has the input scalar value.
Data Types: single | double
Sensor axes skew in percentage, specified as a scalar, a 3-element row vector, or a 3-by-3 matrix. The diagonal elements of the matrix account for the misalignment effects for each axes. The off-diagonal elements account for the cross-axes misalignment effects. The measured state vmeasure is obtained from the true state vtrue via the misalignment matrix as:
If you specify the property as a scalar, then all the off-diagonal elements of the matrix take the value of the specified scalar and all the diagonal elements are 100.
If you specify the property as a vector [a b c], then m21 = m31 = a, m12 = m32 = b, and m13 = m23 = c. All the diagonal elements are 100.
Power spectral density of sensor noise in μT/√Hz, specified as a real scalar or 3-element row vector. Any scalar input is converted into a real 3-element row vector where each element has the input scalar value.
Data Types: single | double
Instability of the bias offset in μT, specified as a real scalar or 3-element row vector. Any scalar input is converted into a real 3-element row vector where each element has the input scalar value.
Data Types: single | double
Bias instability filter numerator coefficients, specified as a real-valued row
vector. To specify coefficients for fractal noise, use the fractalcoef
function.
Data Types: single | double
Bias instability filter denominator coefficients, specified as a real-valued row
vector. To specify coefficients for fractal noise, use the fractalcoef
function.
Data Types: single | double
Select the type of random noise as:
double-sided— Random noise coefficients have a scale factor of 2.single-sided— Random noise coefficients have a scale factor of 1.
Data Types: single | double
Integrated white noise of sensor in (μT)*√Hz, specified as a real scalar or 3-element row vector. Any scalar input is converted into a real 3-element row vector where each element has the input scalar value.
Data Types: single | double
Sensor bias from temperature in μT/℃, specified as a real scalar or 3-element row vector. Any scalar input is converted into a real 3-element row vector where each element has the input scalar value.
Data Types: single | double
Scale factor error from temperature in %/℃, specified as a real scalar or real 3-element row vector with values ranging from 0 to 100. Any scalar input is converted into a real 3-element row vector where each element has the input scalar value.
Data Types: single | double
Algorithms
The following algorithm description assumes an NED navigation frame. The accelerometer model
uses the ground-truth orientation and acceleration inputs and the imuSensor
and accelparams
properties to model accelerometer readings.
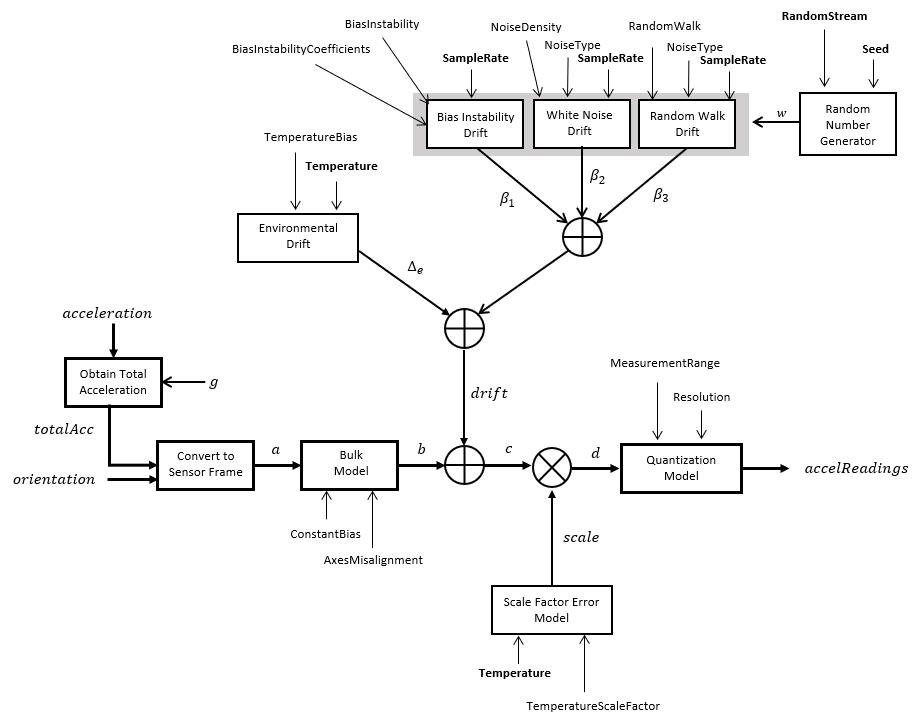
To obtain the total acceleration (totalAcc), the acceleration is preprocessed by negating and adding the gravity constant vector (g= [0; 0; 9.8] m/s2 assuming an NED frame) as:
The acceleration term is negated to obtain zero
total acceleration readings when the accelerometer is in a free fall. The
acceleration term is also known as the specific force.
Then the total acceleration is converted from the local navigation frame to the sensor frame using:
If the orientation is input in quaternion form, it is converted to a rotation matrix before processing.
The ground-truth acceleration in the sensor frame, a, passes through the bulk model, which adds axes misalignment and bias:
where ConstantBias is a property of accelparams, and α1, α2, and α3 are given by the first, second, and third elements of the AxesMisalignment property of accelparams.
The bias instability drift β1 is modeled as white noise biased and then filtered:
where k is the discrete time step index, BiasInstability is
a property of accelparams,
w is white noise that follows a normal distribution of mean 0 and
variance of 1. The discrete time step size is the reciprocal of the SampleRate
property. [g1,
g2, …,
gn+1] are the
denominator coefficients specified in the
BiasInstabilityCoefficients property of the accelparams object.
[f1,
f2, …,
fm+1] are the
numerator coefficients of the BiasInstabilityCoefficients property.
n and m are the orders of the denominator and
numerator coefficients, respectively.
White noise drift is modeled by multiplying elements of the white noise random stream by the standard deviation:
where w is white noise that follows a normal
distribution of mean 0 and variance of 1, SampleRate is an
imuSensor property, and NoiseDensity is an
accelparams property.
The scale variable s = 2 if the NoiseType
property of the accelparams object is
double-sided and s = 1 if the NoiseType
property is single-sided.
The random walk drift is modeled by biasing elements of the white noise random stream and then filtering:
where k is the discrete time step index, RandomWalk is a
property of accelparams, SampleRate is a
property of imuSensor, w is white noise that follows
a normal distribution of mean 0 and variance of 1. The discrete time step size is the
reciprocal of the SampleRate
property. The scale variable s = 2 if the
NoiseType property of the accelparams object is
double-sided and s = 1 if the NoiseType
property is single-sided.
The environmental drift noise is modeled by multiplying the temperature difference from a standard with the temperature bias:
where Temperature is a property of imuSensor, and TemperatureBias is a property of accelparams. The constant 25 corresponds to a standard temperature.
The temperature scale factor error is modeled as:
where Temperature is a property of imuSensor, and TemperatureScaleFactor is a property of accelparams. The constant 25 corresponds to a standard temperature.
The quantization is modeled by first saturating the continuous signal model:
and then setting the resolution:
where MeasurementRange is a property of accelparams.
The following algorithm description assumes an NED navigation frame. The gyroscope model uses
the ground-truth orientation, acceleration, and angular velocity inputs, and the
imuSensor and gyroparams
properties to model accelerometer readings.

The ground-truth angular velocity is converted from the local frame to the sensor frame using the ground-truth orientation:
If the orientation is input in quaternion form, it is converted to a rotation matrix before processing.
The ground-truth angular velocity in the sensor frame, a, passes through the bulk model, which adds axes misalignment and bias:
where ConstantBias is a property of gyroparams, and α1, α2, and α3 are given by the first, second, and third elements of the AxesMisalignment property of gyroparams.
The bias instability drift β1 is modeled as white noise biased and then filtered:
where k is the discrete time step index, BiasInstability is
a property of gyroparams,
w is white noise that follows a normal distribution of mean 0 and
variance of 1. The discrete time step size is the reciprocal of the SampleRate
property. [g1,
g2, …,
gn+1] are the
denominator coefficients specified in the
BiasInstabilityCoefficients property of the gyroparams object.
[f1,
f2, …,
fm+1] are the
numerator coefficients of the BiasInstabilityCoefficients property.
n and m are the orders of the denominator and
numerator coefficients, respectively.
White noise drift is modeled by multiplying elements of the white noise random stream by the standard deviation:
where w is white noise that follows a normal
distribution of mean 0 and variance of 1, SampleRate is an
imuSensor property, and NoiseDensity is an
gyroparams property.
The scale variable s = 2 if the NoiseType
property of the gyroparams object is
double-sided and s = 1 if the NoiseType
property is single-sided.
The random walk drift is modeled by biasing elements of the white noise random stream and then filtering:
where k is the discrete time step index, RandomWalk is a
property of gyroparams, SampleRate is a
property of imuSensor, and w is white noise that
follows a normal distribution of mean 0 and variance of 1. The discrete time step size
is the reciprocal of the SampleRate
property. The scale variable s = 2 if the
NoiseType property of the gyroparams object is
double-sided and s = 1 if the NoiseType
property is single-sided.
The environmental drift noise is modeled by multiplying the temperature difference from a standard with the temperature bias:
where Temperature is a property of imuSensor, and TemperatureBias is a property of gyroparams. The constant 25 corresponds to a standard temperature.
The acceleration bias drift is modeled by multiplying the acceleration input and acceleration bias:
where AccelerationBias is
a property of gyroparams.
The temperature scale factor error is modeled as:
where Temperature is a property of imuSensor, and TemperatureScaleFactor is a property of gyroparams. The constant 25 corresponds to a standard temperature.
The quantization is modeled by first saturating the continuous signal model:
and then setting the resolution:
where MeasurementRange is a property of gyroparams.
The following algorithm description assumes an NED navigation frame. The magnetometer model
uses the ground-truth orientation and acceleration inputs, and the
imuSensor and magparamsmagparams
properties to model magnetometer readings.

The ground-truth acceleration is converted from the local frame to the sensor frame using the ground-truth orientation:
If the orientation is input in quaternion form, it is converted to a rotation matrix before processing.
The ground-truth acceleration in the sensor frame, a, passes through the bulk model, which adds axes misalignment and bias:
where ConstantBias is a property of magparams, and α1, α2, and α3 are given by the first, second, and third elements of the AxesMisalignment property of magparams.
The bias instability drift β1 modeled as white noise biased and then filtered:
where k is the discrete time step index, BiasInstability is
a property of magparams,
w is white noise that follows a normal distribution of mean 0 and
variance of 1. The discrete time step size is the reciprocal of the SampleRate
property. [g1,
g2, …,
gn+1] are the
denominator coefficients specified in the
BiasInstabilityCoefficients property of the magparams object.
[f1,
f2, …,
fm+1] are the
numerator coefficients of the BiasInstabilityCoefficients property.
n and m are the orders of the denominator and
numerator coefficients, respectively.
White noise drift is modeled by multiplying elements of the white noise random stream by the standard deviation:
where w is white noise that follows a normal
distribution of mean 0 and variance of 1, SampleRate is an
imuSensor property, and NoiseDensity is an
magparams property.
The scale variable s = 2 if the NoiseType
property of the magparams object is
double-sided and s = 1 if the NoiseType
property is single-sided.
The random walk drift is modeled by biasing elements of the white noise random stream and then filtering:
where k is the discrete time step index, RandomWalk is a
property of magparams, SampleRate is a
property of imuSensor, w is white noise that follows
a normal distribution of mean 0 and variance of 1. The discrete time step size is the
reciprocal of the SampleRate
property. The scale variable s = 2 if the
NoiseType property of the magparams object is
double-sided and s = 1 if the NoiseType
property is single-sided.
The environmental drift noise is modeled by multiplying the temperature difference from a standard with the temperature bias:
where Temperature is a property of imuSensor, and TemperatureBias is a property of magparams. The constant 25 corresponds to a standard temperature.
The temperature scale factor error is modeled as:
where Temperature is a property of imuSensor, and TemperatureScaleFactor is a property of magparams. The constant 25 corresponds to a standard temperature.
The quantization is modeled by first saturating the continuous signal model:
and then setting the resolution:
where MeasurementRange is a property of magparams.
Extended Capabilities
C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.
Version History
Introduced in R2020aYou can use these new parameters in the Accelerometer, Gyroscope, or Magnetometer tab to specify the coefficients of the transfer function used to generate the bias instability noise and specify the scale factor of the noise coefficients.
Bias instability filter numerator coefficients
Bias instability filter denominator coefficients
Noise type
See Also
Classes
Objects
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)
