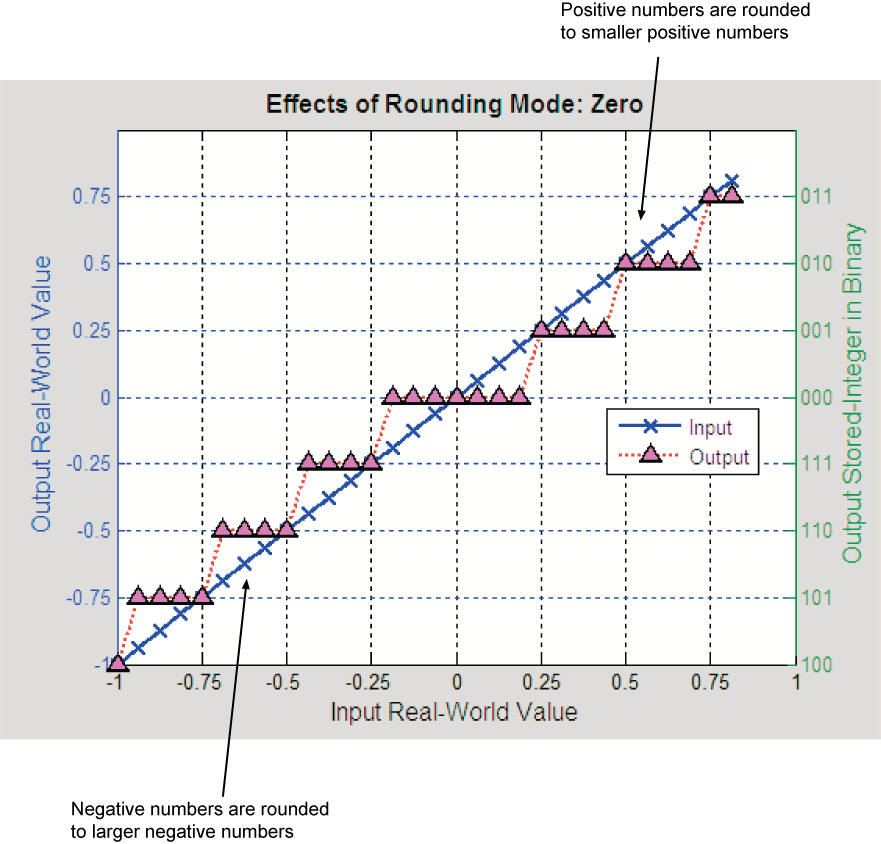
Rounding Mode: Zero
Rounding towards zero is the simplest rounding mode computationally. All digits beyond the number required are dropped. Rounding towards zero results in a number whose magnitude is always less than or equal to the more precise original value.
Rounding toward zero introduces a cumulative downward bias in the result for positive numbers and a cumulative upward bias in the result for negative numbers. That is, all positive numbers are rounded to smaller positive numbers, while all negative numbers are rounded to larger negative numbers.
You can round to zero using the fix function.
Rounding to Zero Versus Truncation
Rounding to zero and truncation or chopping are sometimes thought to mean the same thing. However, the results produced by rounding to zero and truncation are different for unsigned and two's complement numbers. For this reason, the ambiguous term truncation is not used and explicit rounding modes are used instead.
For example, consider rounding a 5-bit unsigned number to zero by dropping (truncating) the two least significant bits. For example, the unsigned number 100.01 = 4.25 is truncated to 100 = 4. Therefore, truncating an unsigned number is equivalent to rounding to zero or rounding to floor.
Now consider rounding a 5-bit two's complement number by dropping the two least significant bits. At first glance, you may think truncating a two's complement number is the same as rounding to zero. For example, dropping the last two digits of -3.75 yields -3.00. However, digital hardware performing two's complement arithmetic yields a different result. Specifically, the number 100.01 = -3.75 truncates to 100 = -4, which is rounding to floor.