Implement Hardware-Efficient Complex Partial-Systolic Q-less QR with Forgetting Factor
This example shows how to use the hardware-efficient Complex Partial-Systolic Q-less QR Decomposition with Forgetting Factor block.
Q-less QR Decomposition with Forgetting Factor
The Complex Partial-Systolic Q-less QR Decomposition with Forgetting Factor block implements the following recursion to compute the upper-triangular factor R of continuously streaming n-by-1 row vectors A(k,:) using forgetting factor  . It is as if matrix A is infinitely tall. The forgetting factor in the range
. It is as if matrix A is infinitely tall. The forgetting factor in the range  keeps it from integrating without bound.
keeps it from integrating without bound.
![$$ \begin{array}{rcl} R_0 &=& \mbox{zeros}(n,n)\\[2ex] [\sim\;,\;R_1] &=& \mbox{qr}\left(\left[\begin{array}{c}R_0\\ A(1,:)\end{array}\right],\; 0\right)\\ R_1 &=& \alpha R_1\\[4ex] [\sim\;,\;R_2] &=& \mbox{qr}\left(\left[\begin{array}{c}R_1\\ A(2,:)\end{array}\right],\; 0\right)\\ R_2 &=& \alpha R_2\\[4ex] \vdots\\[4ex] [\sim\;,\;R_k] &=& \mbox{qr}\left(\left[\begin{array}{c}R_{k-1}\\ A(k,:)\end{array}\right],\; 0\right)\\ R_k &=& \alpha R_k\\[4ex] \vdots\\[4ex] \end{array} $$](../../examples/fixedpoint/win64/ComplexPartialSystolicQlessQRForgettingFactorExample_eq09306810281325018698.png)
AMBA AXI Handshaking Process
The Data Handler subsystem in this model takes complex matrix A as input. It sends rows of A to the QR Decomposition block using the AMBA AXI handshake protocol. The validIn signal indicates when data is available. The ready signal indicates that the block can accept the data. Transfer of data occurs only when both the validIn and ready signals are high. You can set delay for the feeding in rows of A in the Data Handler to emulate the processing time of the upstream block. validOut signal of the Data Handler remain high when rowDelay is set to 0 because this indicates the Data Handler always has data available.
Define System Parameters
n is the length of the row vectors A(k,:) and the number of rows and columns in R.
n = 5;
m is the effective number of rows of A to integrate over.
m = 100;
Use the fixed.forgettingFactor function to compute the forgetting factor as a function of the number of rows that you are integrating over.
forgettingFactor = fixed.forgettingFactor(m)
forgettingFactor =
0.9950
precisionBits defines the number of bits of precision required for the QR Decomposition. Set this value according to system requirements.
precisionBits = 24;
In this example, complex-valued matrix A is constructed such that the magnitude of the real and imaginary parts of its elements is less than or equal to one, so the maximum possible absolute value of any element is  . Your own system requirements will define what those values are. If you don't know what they are, and A is a fixed-point input to the system, then you can use the
. Your own system requirements will define what those values are. If you don't know what they are, and A is a fixed-point input to the system, then you can use the upperbound function to determine the upper bounds of the fixed-point types of A.
max_abs_A is an upper bound on the maximum magnitude element of A.
max_abs_A = sqrt(2);
Select Fixed-Point Types
Use the fixed.qlessqrFixedpointTypes function to compute fixed-point types.
T = fixed.qlessqrFixedpointTypes(m,max_abs_A,precisionBits)
T =
struct with fields:
A: [0×0 embedded.fi]
T.A is the fixed-point type computed for transforming A to R in-place so that it does not overflow.
T.A
ans =
[]
DataTypeMode: Fixed-point: binary point scaling
Signedness: Signed
WordLength: 31
FractionLength: 24
Define Simulation Parameters
Create random matrix A to contain a specified number of inputs.
numInputs is the number of input rows A(k,:) for this example.
numInputs = 500;
rng('default')
A = fixed.example.complexUniformRandomArray(-1,1,numInputs,n);
Cast the inputs to the types determined by fixed.qlessqrFixedpointTypes.
A = cast(A,'like',T.A);
Cast the forgetting factor to a fixed-point type with the same word length as A and best-precision scaling.
forgettingFactor = fi(forgettingFactor,1,T.A.WordLength);
rowDelay = 1; % Delay of clock cycles between feeding in rows of A
Select a stop time for the simulation that is long enough to process all the inputs from A.
stopTime = 4*numInputs*T.A.WordLength;
Open the Model
model = 'ComplexPartialSystolicQlessQRForgettingFactorModel';
open_system(model);
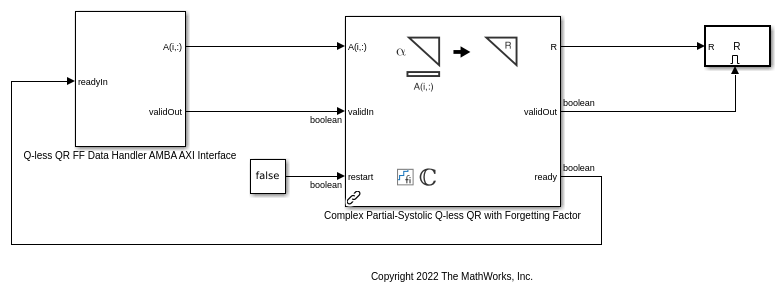
Set Variables in the Model Workspace
Use the helper function setModelWorkspace to add the variables defined above to the model workspace.
fixed.example.setModelWorkspace(model,'A',A,'n',n,... 'forgettingFactor',forgettingFactor,... 'regularizationParameter',0,... 'rowDelay',rowDelay,... 'stopTime',stopTime);
Simulate the Model
out = sim(model);
Verify the Accuracy of the Output
Define matrix  as follows
as follows
![$$A_k = \left[\begin{array}{cccc}\alpha^k \\& \alpha^{k-1} \\ & & \ddots\\& & & \alpha\end{array}\right]A(1:k,\; :).$$](../../examples/fixedpoint/win64/ComplexPartialSystolicQlessQRForgettingFactorExample_eq14596989301175552323.png)
Then using the formula for the computation of the 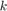 th output
th output 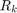 , and the fact that
, and the fact that ![$[Q,R]=\mbox{qr}(A,0) \Rightarrow A'A = R'Q'QR = R'R$](../../examples/fixedpoint/win64/ComplexPartialSystolicQlessQRForgettingFactorExample_eq09072293385473654700.png) , you can show that
, you can show that
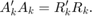
So to verify the output, the difference between 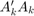 and
and 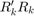 should be small.
should be small.
Choose the last output of the simulation.
R = double(out.R(:,:,end))
R = Columns 1 through 4 7.8025 + 0.0000i 0.3158 + 0.0965i -0.0992 + 0.2743i 0.7696 + 0.2507i 0.0000 + 0.0000i 7.8339 + 0.0000i -0.3554 - 0.4953i -0.4352 - 0.3383i 0.0000 + 0.0000i 0.0000 + 0.0000i 8.1951 + 0.0000i -0.2289 - 0.0269i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 8.0860 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i 0.0000 + 0.0000i Column 5 -0.2899 - 0.2469i -0.4371 - 0.7667i -0.3997 + 0.4916i 0.1868 + 0.0171i 7.9768 + 0.0000i
Verify that R is upper triangular.
isequal(R,triu(R))
ans = logical 1
Verify that the diagonal is greater than or equal to zero.
diag(R)
ans =
7.8025
7.8339
8.1951
8.0860
7.9768
Synchronize the last output R with the input by finding the number of inputs that produced it.
A = double(A); alpha = double(forgettingFactor); relative_errors = nan(1,n); for k = 1:numInputs A_k = alpha.^(k:-1:1)' .* A(1:k,:); relative_errors(k) = norm(A_k'*A_k - R'*R)/norm(A_k'*A_k); end
k is the number of inputs A(k,:) that produced the last R.
k = find(relative_errors==min(relative_errors),1,'last')
k = 500
Verify that

with a small relative error.
A_k = alpha.^(k:-1:1)' .* A(1:k,:); relative_error = norm(A_k'*A_k - R'*R)/norm(A_k'*A_k)
relative_error = 7.3665e-06
Suppress mlint warnings in this file.
%#ok<*NOPTS>
See Also
Complex Partial-Systolic Q-less QR Decomposition with Forgetting Factor