Forecast State-Space Model Using Monte-Carlo Methods
This example shows how to forecast a state-space model using Monte-Carlo methods, and to compare the Monte-Carlo forecasts to the theoretical forecasts.
Suppose that the relationship between the change in the unemployment rate () and the nominal gross national product (nGNP) growth rate () can be expressed in the following, state-space model form.
where:
is the change in the unemployment rate at time t.
is a dummy state for the MA(1) effect on .
is the nGNP growth rate at time t.
is a dummy state for the MA(1) effect on .
is the observed change in the unemployment rate.
is the observed nGNP growth rate.
and are Gaussian series of state disturbances having mean 0 and standard deviation 1.
is the Gaussian series of observation innovations having mean 0 and standard deviation .
is the Gaussian series of observation innovations having mean 0 and standard deviation .
Load the Nelson-Plosser data set, which contains the unemployment rate and nGNP series, among other things.
load Data_NelsonPlosserPreprocess the data by taking the natural logarithm of the nGNP series, and the first difference of each. Also, remove the starting NaN values from each series.
isNaN = any(ismissing(DataTable),2); % Flag periods containing NaNs gnpn = DataTable.GNPN(~isNaN); u = DataTable.UR(~isNaN); T = size(gnpn,1); % Sample size y = zeros(T-1,2); % Preallocate y(:,1) = diff(u); y(:,2) = diff(log(gnpn));
This example proceeds using series without NaN values. However, using the Kalman filter framework, the software can accommodate series containing missing values.
To determine how well the model forecasts observations, remove the last 10 observations for comparison.
numPeriods = 10; % Forecast horizon isY = y(1:end-numPeriods,:); % In-sample observations oosY = y(end-numPeriods+1:end,:); % Out-of-sample observations
Specify the coefficient matrices.
A = [NaN NaN NaN 0; 0 0 0 0; NaN 0 NaN NaN; 0 0 0 0]; B = [1 0; 1 0; 0 1; 0 1]; C = [1 0 0 0; 0 0 1 0]; D = [NaN 0; 0 NaN];
Specify the state-space model using ssm. Verify that the model specification is consistent with the state-space model.
Mdl = ssm(A,B,C,D)
Mdl = State-space model type: ssm State vector length: 4 Observation vector length: 2 State disturbance vector length: 2 Observation innovation vector length: 2 Sample size supported by model: Unlimited Unknown parameters for estimation: 8 State variables: x1, x2,... State disturbances: u1, u2,... Observation series: y1, y2,... Observation innovations: e1, e2,... Unknown parameters: c1, c2,... State equations: x1(t) = (c1)x1(t-1) + (c3)x2(t-1) + (c4)x3(t-1) + u1(t) x2(t) = u1(t) x3(t) = (c2)x1(t-1) + (c5)x3(t-1) + (c6)x4(t-1) + u2(t) x4(t) = u2(t) Observation equations: y1(t) = x1(t) + (c7)e1(t) y2(t) = x3(t) + (c8)e2(t) Initial state distribution: Initial state means are not specified. Initial state covariance matrix is not specified. State types are not specified.
Estimate the model parameters, and use a random set of initial parameter values for optimization. Restrict the estimate of and to all positive, real numbers using the 'lb' name-value pair argument. For numerical stability, specify the Hessian when the software computes the parameter covariance matrix, using the 'CovMethod' name-value pair argument.
rng(1); params0 = rand(8,1); [EstMdl,estParams] = estimate(Mdl,isY,params0,... 'lb',[-Inf -Inf -Inf -Inf -Inf -Inf 0 0],'CovMethod','hessian');
Method: Maximum likelihood (fmincon)
Sample size: 51
Logarithmic likelihood: -170.92
Akaike info criterion: 357.84
Bayesian info criterion: 373.295
| Coeff Std Err t Stat Prob
----------------------------------------------------
c(1) | 0.06750 0.16548 0.40791 0.68334
c(2) | -0.01372 0.05887 -0.23302 0.81575
c(3) | 2.71201 0.27039 10.03006 0
c(4) | 0.83816 2.84586 0.29452 0.76836
c(5) | 0.06274 2.83470 0.02213 0.98234
c(6) | 0.05196 2.56873 0.02023 0.98386
c(7) | 0.00272 2.40771 0.00113 0.99910
c(8) | 0.00016 0.13942 0.00113 0.99910
|
| Final State Std Dev t Stat Prob
x(1) | -0.00000 0.00272 -0.00033 0.99973
x(2) | 0.12237 0.92954 0.13164 0.89527
x(3) | 0.04049 0.00016 256.77783 0
x(4) | 0.01183 0.00016 72.52162 0
EstMdl is an ssm model, and you can access its properties using dot notation.
Filter the estimated, state-space model, and extract the filtered states and their variances from the final period.
[~,~,Output] = filter(EstMdl,isY);
Modify the estimated, state-space model so that the initial state means and covariances are the filtered states and their covariances of the final period. This sets up simulation over the forecast horizon.
EstMdl1 = EstMdl; EstMdl1.Mean0 = Output(end).FilteredStates; EstMdl1.Cov0 = Output(end).FilteredStatesCov;
Simulate 5e5 paths of observations from the fitted, state-space model EstMdl. Specify to simulate observations for each period.
numPaths = 5e5;
SimY = simulate(EstMdl1,10,'NumPaths',numPaths);SimY is a 10-by- 2-by- numPaths array containing the simulated observations. The rows of SimY correspond to periods, the columns correspond to an observation in the model, and the pages correspond to paths.
Estimate the forecasted observations and their 95% confidence intervals in the forecast horizon.
MCFY = mean(SimY,3); CIFY = quantile(SimY,[0.025 0.975],3);
Estimate the theoretical forecast bands.
[Y,YMSE] = forecast(EstMdl,10,isY); Lb = Y - sqrt(YMSE)*1.96; Ub = Y + sqrt(YMSE)*1.96;
Plot the forecasted observations with their true values and the forecast intervals.
figure h = plot(dates(end-numPeriods-9:end),[isY(end-9:end,1);oosY(:,1)],'-k',... dates(end-numPeriods+1:end),MCFY(end-numPeriods+1:end,1),'.-r',... dates(end-numPeriods+1:end),CIFY(end-numPeriods+1:end,1,1),'-b',... dates(end-numPeriods+1:end),CIFY(end-numPeriods+1:end,1,2),'-b',... dates(end-numPeriods+1:end),Y(:,1),':c',... dates(end-numPeriods+1:end),Lb(:,1),':m',... dates(end-numPeriods+1:end),Ub(:,1),':m',... 'LineWidth',3); xlabel('Period') ylabel('Change in the unemployment rate') legend(h([1,2,4:6]),{'Observations','MC forecasts',... '95% forecast intervals','Theoretical forecasts',... '95% theoretical intervals'},'Location','Best') title('Observed and Forecasted Changes in the Unemployment Rate')
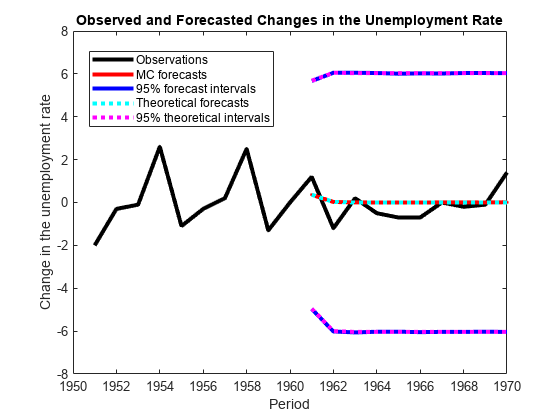
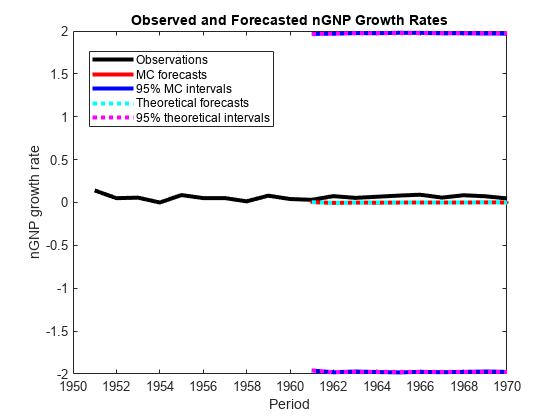
figure h = plot(dates(end-numPeriods-9:end),[isY(end-9:end,2);oosY(:,2)],'-k',... dates(end-numPeriods+1:end),MCFY(end-numPeriods+1:end,2),'.-r',... dates(end-numPeriods+1:end),CIFY(end-numPeriods+1:end,2,1),'-b',... dates(end-numPeriods+1:end),CIFY(end-numPeriods+1:end,2,2),'-b',... dates(end-numPeriods+1:end),Y(:,2),':c',... dates(end-numPeriods+1:end),Lb(:,2),':m',... dates(end-numPeriods+1:end),Ub(:,2),':m',... 'LineWidth',3); xlabel('Period') ylabel('nGNP growth rate') legend(h([1,2,4:6]),{'Observations','MC forecasts',... '95% MC intervals','Theoretical forecasts','95% theoretical intervals'},... 'Location','Best') title('Observed and Forecasted nGNP Growth Rates')
See Also
ssm | simulate | estimate | refine | forecast