Estimate a Regression Model with Multiplicative ARIMA Errors
This example shows how to fit a regression model with multiplicative ARIMA errors to data using estimate.
Load the airline and recession data sets. Plot the monthly passenger totals and the log of the totals.
load Data_Airline load Data_Recessions y = DataTimeTable.PSSG; logY = log(y); figure tiledlayout(2,1) nexttile plot(DataTimeTable.Time,y) title('{\bf Monthly Passenger Totals (Jan1949 - Dec1960)}') nexttile plot(DataTimeTable.Time,log(y)) title('{\bf Monthly Passenger Log-Totals (Jan1949 - Dec1960)}')

The log transformation seems to linearize the time series.
Construct the predictor (X), which is whether the country was in a recession during the sampled period. A 0 in row t means the country was not in a recession in month t, and a 1 in row t means that it was in a recession in month t.
X = zeros(numel(dates),1); % Preallocation for j = 1:size(Recessions,1) X(dates >= Recessions(j,1) & dates <= Recessions(j,2)) = 1; end
Fit the simple linear regression model
to the data.
EstMdl = fitlm(X,logY);
Fit is a LinearModel that contains the least squares estimates.
Check for standard linear model assumption departures by plotting the residuals several ways.
figure tiledlayout(2,2) nexttile plotResiduals(EstMdl,'caseorder','ResidualType','Standardized',... 'LineStyle','-','MarkerSize',0.5) nexttile plotResiduals(EstMdl,'lagged','ResidualType','Standardized') nexttile plotResiduals(EstMdl,'probability','ResidualType','Standardized') nexttile plotResiduals(EstMdl,'histogram','ResidualType','Standardized')

r = EstMdl.Residuals.Standardized; figure tiledlayout(2,1) nexttile autocorr(r) nexttile parcorr(r)

The residual plots indicate that the unconditional disturbances are autocorrelated. The probability plot and histogram seem to indicate that the unconditional disturbances are Gaussian.
The ACF of the residuals confirms that the unconditional disturbances are autocorrelated.
Take the 1st difference of the residuals and plot the ACF and PACF of the differenced residuals.
dR = diff(r); figure tiledlayout(2,1) nexttile autocorr(dR,'NumLags',50) nexttile parcorr(dR,'NumLAgs',50)

The ACF shows that there are significantly large autocorrelations, particularly at every 12th lag. This indicates that the unconditional disturbances have 12th degree seasonal integration.
Take the first and 12th differences of the residuals. Plot the differenced residuals, and their ACF and PACF.
DiffPoly = LagOp([1 -1]); SDiffPoly = LagOp([1 -1],'Lags',[0, 12]); diffR = filter(DiffPoly*SDiffPoly,r); figure tiledlayout("flow") nexttile([1 2]) plot(diffR) axis tight nexttile autocorr(diffR) h = gca; h.FontSize = 7; nexttile parcorr(diffR) h = gca; h.FontSize = 7;
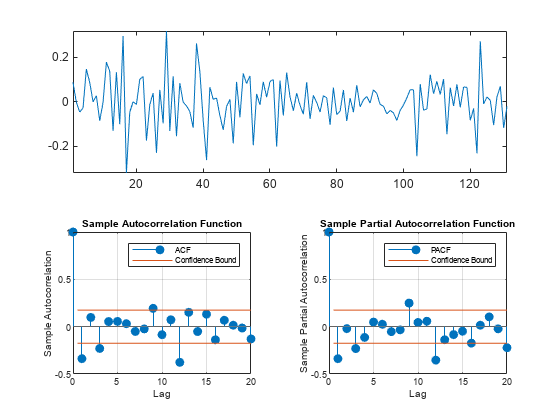
The residuals resemble white noise (with possible heteroscedasticity). According to Box and Jenkins (1994), Chapter 9, the ACF and PACF indicate that the unconditional disturbances are an model.
Specify the regression model with errors:
Mdl = regARIMA('MALags',1,'D',1,'Seasonality',12,'SMALags',12)
Mdl =
regARIMA with properties:
Description: "ARIMA(0,1,1) Error Model Seasonally Integrated with Seasonal MA(12) (Gaussian Distribution)"
SeriesName: "Y"
Distribution: Name = "Gaussian"
Intercept: NaN
Beta: [1×0]
P: 13
D: 1
Q: 13
AR: {}
SAR: {}
MA: {NaN} at lag [1]
SMA: {NaN} at lag [12]
Seasonality: 12
Variance: NaN
Partition the data set into the presample and estimation sample so that you can initialize the series. P = Q = 13, so the presample should be at least 13 periods long.
preLogY = logY(1:13); % Presample responses estLogY = logY(14:end); % Estimation sample responses preX = X(1:13); % Presample predictors estX = X(14:end); % Estimation sample predictors
Obtain presample unconditional disturbances from a linear regression of the presample data.
PreFit = fitlm(preX,preLogY);... % Presample fit for presample residuals EstFit = fitlm(estX,estLogY);... % Estimation sample fit for the intercept U0 = PreFit.Residuals.Raw;
If the error model is integrated, then the regression model intercept is not identifiable. Set Intercept to the estimated intercept from a linear regression of the estimation sample data. Estimate the regression model with IMA errors.
Mdl.Intercept = EstFit.Coefficients{1,1};
EstMdl = estimate(Mdl,estLogY,'X',estX,'U0',U0);
Regression with ARIMA(0,1,1) Error Model Seasonally Integrated with Seasonal MA(12) (Gaussian Distribution):
Value StandardError TStatistic PValue
_________ _____________ __________ __________
Intercept 5.5722 0 Inf 0
MA{1} -0.025366 0.22197 -0.11427 0.90902
SMA{12} -0.80255 0.052705 -15.227 2.3349e-52
Beta(1) 0.0027588 0.10139 0.02721 0.97829
Variance 0.0072463 0.00015974 45.365 0
MA{1} and Beta1 are not significantly different from 0. You can remove these parameters from the model, possibly add other parameters (e.g., AR parameters), and compare multiple model fits using aicbic. Note that the estimation and presample should be the same over competing models.
References:
Box, G. E. P., G. M. Jenkins, and G. C. Reinsel. Time Series Analysis: Forecasting and Control. 3rd ed. Englewood Cliffs, NJ: Prentice Hall, 1994.