Calculate Mean Square Error Performance Using LMS Filter
This example shows how use the LMS Filter block to calculate the mean square error performance in additive white Gaussian noise (AWGN). The block supports scalar and vector inputs of type real or complex. You can generate the HDL code from the LMSFilter subsystem in this Simulink® model.
Set Up Input Variables
Set up these workspace variables for the model. These variables configure the LMS Filter block.
filterLength = 64; stepSize = 0.2/(1*filterLength); % recommended step size is less than % 1/(2 x power of input signal x filter length) vecSize = 2; inptType = 1; % 0 means real; 1 means complex niter = 20; % number of iterations to run for calculating mean square error frameSize = 2800; simtime = frameSize/vecSize + 100; errSumAbsSq = zeros(1,frameSize); errRefSumAbsSq = zeros(1,frameSize);
Generate Input Data and Run Model
Generate input data for the LMS Filter block and the reference System object™ dsp.LMSFilter for niter number of iterations.
for k = 1:niter % Create filter object filterObj = dsp.FIRFilter; num = normalize(randn(1,filterLength) + inptType*1i*randn(1,filterLength))/sqrt(filterLength); filterObj.Numerator = num; % Use dsp.LMSFilter object for reference lmsfilt = dsp.LMSFilter(filterLength, 'StepSize', stepSize); % Generate input data observedSignal = fi(randn(frameSize,1,'like',num),1,18,15); noise = 0.012*randn(frameSize,1); validIn = true(frameSize,1); % Generate desired signal by adding noise to filtered data desiredSignal = fi(filterObj(double(observedSignal)) + noise,1,18,15); % Capture reference output values and calculate average of absolute square error [filtOutRef,errRef,wtsRef] = lmsfilt(double(observedSignal),double(desiredSignal)); errRefSumAbsSq = errRefSumAbsSq + abs(errRef(1:frameSize)).^2.'; % Simulate model LMSModel = 'HDLLMSBlock'; load_system(LMSModel);% run this command to open the model lms = sim(LMSModel); % Capture model output and calculate average of absolute square error validOut = squeeze(lms.validOut); errOutLMS = squeeze(double(lms.errOut)).'; if vecSize ==1 errOutAbsSq = abs(errOutLMS(:,validOut)).^2.'; else errOutAbsSq = abs(errOutLMS(validOut,:)).^2.'; end errOutAbsSq = errOutAbsSq(:).'; errSumAbsSq = errSumAbsSq + errOutAbsSq(1:frameSize); % To reset the internal states of the object reset(filterObj) reset(lmsfilt) end
Plot Mean Square Error
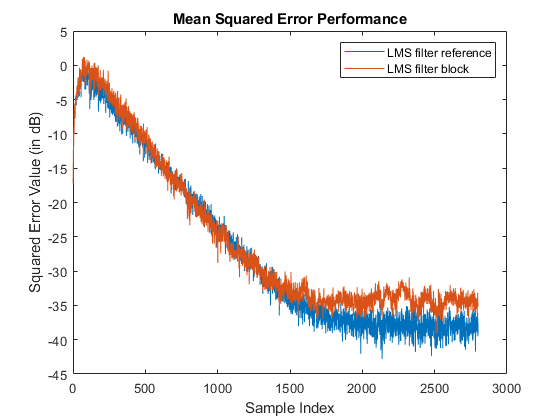
Plot the mean square error in dB against the LMS Filter block output and the LMS filter reference output.
meanSqErrRefLMS_dB = 10*log10(errRefSumAbsSq/niter); meanSqErrLMS_dB = 10*log10(errSumAbsSq/niter); figure plot(meanSqErrRefLMS_dB) hold on plot(meanSqErrLMS_dB) title('Mean Squared Error Performance') xlabel('Sample Index') ylabel('Squared Error Value (in dB)') legend('LMS filter reference','LMS filter block')