Zoom FFT

This example showcases zoom FFT, which is a signal processing technique used to analyze a portion of a spectrum at a high resolution. The DSP System Toolbox™ offers this functionality in MATLAB® through the dsp.ZoomFFT System object™, and in Simulink® through the Zoom FFT library block.

The Limitation of Standard DFT/FFT

A digital signal's spectral resolution is determined (hence bounded) by its length. We will illustrate this fact with a simple example. Consider a signal formed by the sum of two sine waves:

L   = 32;       % Frame size
Fs  = 128;      % Sample rate
res = Fs/L;     % Frequency resolution
f1  = 40;       % First sine wave frequency
f2  = f1 + res; % Second sine wave frequency
 
sn1 = dsp.SineWave(Frequency=f1, SampleRate=Fs, SamplesPerFrame=L);
sn2 = dsp.SineWave(Frequency=f2, SampleRate=Fs, SamplesPerFrame=L, Amplitude=2);

x = sn1() + sn2();

Compute the FFT of x and plot the magnitude of the FFT. Note that the two sine waves are in adjacent samples of the FFT. This means that you cannot discriminate between frequencies closer than $\frac{{\mathrm{F}}_{\mathit{s}}}{\mathit{L}}$.

X = fft(x);
scopeFFT = dsp.ArrayPlot(SampleIncrement=Fs/L, ...
    XOffset=-Fs/2, ...
    XLabel="Frequency (Hz)", ...
    YLabel="Magnitude", ...
    Title="Two-sided spectrum", ...
    YLimits=[-0.1 1.1]);
scopeFFT(abs(fftshift(X))/L);

Zoom FFT

Suppose you have an application for which you are only interested in a sub-band of the Nyquist interval. The idea behind zoom FFT is to retain the same resolution you would achieve with a full size FFT on your original signal by computing a small FFT on a shorter signal. The shorter signal comes from decimating the original signal. The savings come from being able to compute a much shorter FFT while achieving the same resolution. This is intuitive: for a decimation factor of D, the new sampling rate is ${\mathit{F}}_{\mathrm{sd}}=\frac{{\mathrm{F}}_{\mathit{s}}}{\mathit{D}}$, and the new frame size (and FFT length) is ${\mathit{L}}_{\mathit{d}}=\frac{\mathit{L}}{\mathit{D}}$, so the resolution of the decimated signal is $\frac{{\mathit{F}}_{\mathrm{sd}}}{{\mathit{L}}_{\mathit{d}}}=\frac{{\mathrm{F}}_{\mathit{s}}}{\mathit{L}}$.

The DSP System Toolbox offers zoom FFT functionality for MATLAB and Simulink, through the dsp.ZoomFFT System object and the zoom FFT library block, respectively. The next sections will discuss the zoom FFT algorithm in more detail.

The Mixer Approach

Before discussing the algorithm used in dsp.ZoomFFT, we present the mixer approach, which is a popular zoom FFT method.

For the example here, assume you are only interested in the interval [16 Hz, 48 Hz].

BWOfInterest = 48 - 16;
Fc           = (16 + 48)/2; % Center frequency of bandwidth of interest

The achievable decimation factor is:

BWFactor = floor(Fs/BWOfInterest)

BWFactor = 4

The mixer approach consists of first shifting the band of interest down to DC using a mixer, followed by lowpass filtering and decimation by a factor of BWFactor.

Design the decimation filter's coefficients using the designMultirateFIR function. The dsp.FIRDecimator System object implements the lowpass and downsampling using an efficient polyphase FIR decimation structure.

B = designMultirateFIR(1, BWFactor);
D = dsp.FIRDecimator(BWFactor, B);

Now, mix the signal down to DC, and filter it through the FIR decimator:

% Run several input frames to eliminate the FIR transient response
for k = 1:10
    % Grab a frame of the input signal
    x = sn1()+sn2();

    % Downmix to DC
    indVect = (0:numel(x)-1).' + (k-1) * size(x,1);
    y = x .* exp(-2*pi*indVect*Fc*1j/Fs);

    % Filter through FIR decimator
    xd = D(y);    
end

Now take the FFT of the filtered signal (note that the FFT length is reduced by BWFactor, or the decimation length, compared to regular FFT, while maintaining the same resolution):

Xd  = fft(xd);
Ld  = L/BWFactor;
Fsd = Fs/BWFactor;

scopeMixing = dsp.ArrayPlot(SampleIncrement=Fs/L, ...
    XOffset=Fsd/2, ...
    XLabel="Frequency (Hz)", ...
    YLabel="Magnitude", ...
    Title="Zoom FFT Spectrum: Mixer Approach", ...
    YLimits=[-0.1 1.1]);

scopeMixing(abs(fftshift(Xd))/Ld);

The complex-valued mixer adds an extra multiplication for each high-rate sample, which is not efficient. The next section presents an alternative, more efficient, zoom FFT approach.

Bandpass Sampling

An alternative zoom FFT method takes advantage of a known result from bandpass filtering (also sometimes called under-sampling): Assume we are interested in the band $\left[{\mathit{F}}_1,{\mathit{F}}_2\right],$of a signal with sampling rate ${\mathit{F}}_{\mathit{s}}$. If we pass the signal through a complex (one-sided) bandpass filter centered at ${\mathit{F}}_{\mathit{c}}=\frac{{\mathit{F}}_1+{\mathit{F}}_2}{2}$ and with bandwidth $\mathrm{BW}={\mathit{F}}_2-{\mathit{F}}_1$, and then downsample it by a factor of $D=\lfloor \frac{{\mathit{F}}_{\mathit{s}}}{\mathrm{BW}}\rfloor$, we will bring down the desired band to baseband.

In general, if ${\mathit{F}}_{\mathit{c}}$ cannot be expressed in the form $k\frac{{\mathit{F}}_{\mathit{s}}}{\mathit{D}}$ (where K is an integer), then the shifted, decimated spectrum will not be centered at DC. In fact, the center frequency Fc will be translated to [2]:

$${\mathit{F}}_{\mathit{d}}={\mathit{F}}_{\mathit{c}}-\frac{{\mathit{F}}_{\mathit{s}}}{\mathit{D}}\lfloor \frac{\mathit{D}\cdot {\mathit{F}}_{\mathit{c}}+{\mathit{F}}_{\mathit{s}}/2}{{\mathit{F}}_{\mathit{s}}}\rfloor$$

In this case, we can use a mixer (running at the low sample rate of the decimated signal) to center the desired band to zero Hertz.

Using the example from the previous section, we obtain the coefficients of the complex bandpass filter by modulating the coefficients of the designed lowpass filter:

N   = length(D.Numerator);
Bbp = B .*exp(1j*(Fc / Fs)*2*pi*(0:N-1));
Dbp = dsp.FIRDecimator(BWFactor, Bbp);

Now perform the filtering and the FFT:

for k = 1:10
    % Run a few times to eliminate transient in filter
    x = sn1()+sn2();
    xd = Dbp(x);    
end
Xd = fft(xd);
scopeBandpassSampling = dsp.ArrayPlot(SampleIncrement=Fs/L, ...
    XOffset=Fsd/2, ...
    XLabel="Frequency (Hz)", ...
    YLabel="Magnitude", ...
    Title="Zoom FFT Spectrum: Bandpass Sampling Approach", ...
    YLimits=[-0.1 1.1]);
scopeBandpassSampling(abs(fftshift(Xd))/Ld);

Using a Multirate, Multistage Bandpass Filter

The FIR decimator used in the previous section is a single-stage multirate filter. We can reduce the computational complexity of the filter by using a multistage design instead (in fact, this is the approach utilized in dsp.ZoomFFT). See Multistage Rate Conversion for more details.

Consider the following example, where the input sample rate is 48 KHz, and the bandwidth of interest is the interval [1500,2500] Hz. The achievable decimation factor is then $\lfloor \frac{48000}{1000}\rfloor =48$.

First, design a single-stage decimator:

Fs       = 48e3;
Fc       = 2000; % Bandpass filter center frequency
BW       = 1e3;  % Bandwidth of interest
Ast      = 80;   % Stopband attenuation
P        = 12;   % Polyphase length
BWFactor = floor(Fs/BW);
B        = designMultirateFIR(1,BWFactor,P,Ast);
N        = length(B);
Bbp      = B .*exp(1j*(Fc / Fs)*2*pi*(0:N-1));
D_single_stage = dsp.FIRDecimator(BWFactor, Bbp);

Now, implement the same decimator using a multistage design, while maintaining the same stopband attenuation and transition bandwidth as the single-stage case (see kaiserord for details on the transition width computation):

tw = (Ast - 7.95) / ( N * 2.285);
D_multi_stage = designMultistageDecimator(BWFactor, Fs, tw*Fs/(2*pi), Ast);
fprintf("Number of filter stages: %d\n", getNumStages(D_multi_stage) );

Number of filter stages: 5

for ns=1:D_multi_stage.getNumStages
    stgn = D_multi_stage.("Stage" + ns);
    fprintf("Stage %i: Decimation factor = %d , FIR length = %d\n",...
            ns, stgn.DecimationFactor,...
            length(stgn.Numerator));
end

Stage 1: Decimation factor = 2 , FIR length = 7
Stage 2: Decimation factor = 2 , FIR length = 7
Stage 3: Decimation factor = 2 , FIR length = 11
Stage 4: Decimation factor = 2 , FIR length = 15
Stage 5: Decimation factor = 3 , FIR length = 75

Note that D_multi_stage is a five-stage multirate lowpass filter. We transform it to a bandpass filter by performing a frequency shift on the coefficients of each stage, while taking the cumulative decimation factor into account:

Mn = 1; % Cumulative decimation factor entring stage n
for ns=1:D_multi_stage.getNumStages
    stgn = D_multi_stage.("Stage" + ns);
    num  = stgn.Numerator;
    N    = length(num);
    num  = num .*exp(1j*(Fc * Mn/ Fs)*2*pi*(0:N-1));
    stgn.Numerator = num;
    Mn   = Mn*stgn.DecimationFactor;
end

Comparing the cost of the single-stage and multistage filters, the latter is significantly more computationally efficient.

For the single-stage filter, this cost is:

cost(D_single_stage)

ans = struct with fields:
                  NumCoefficients: 1129
                        NumStates: 1104
    MultiplicationsPerInputSample: 23.5208
          AdditionsPerInputSample: 23.5000

Whereas the multistage filter has the cost:

cost(D_multi_stage)

ans = struct with fields:
                  NumCoefficients: 77
                        NumStates: 108
    MultiplicationsPerInputSample: 6.2500
          AdditionsPerInputSample: 5.2917

Next, compare the frequency response of the two filters, and verify they have the same passband characteristics. The differences in the stopband are negligible.

vis = fvtool(D_single_stage,D_multi_stage,DesignMask="off",legend="on");
legend(vis,"Single-stage","Multistage")

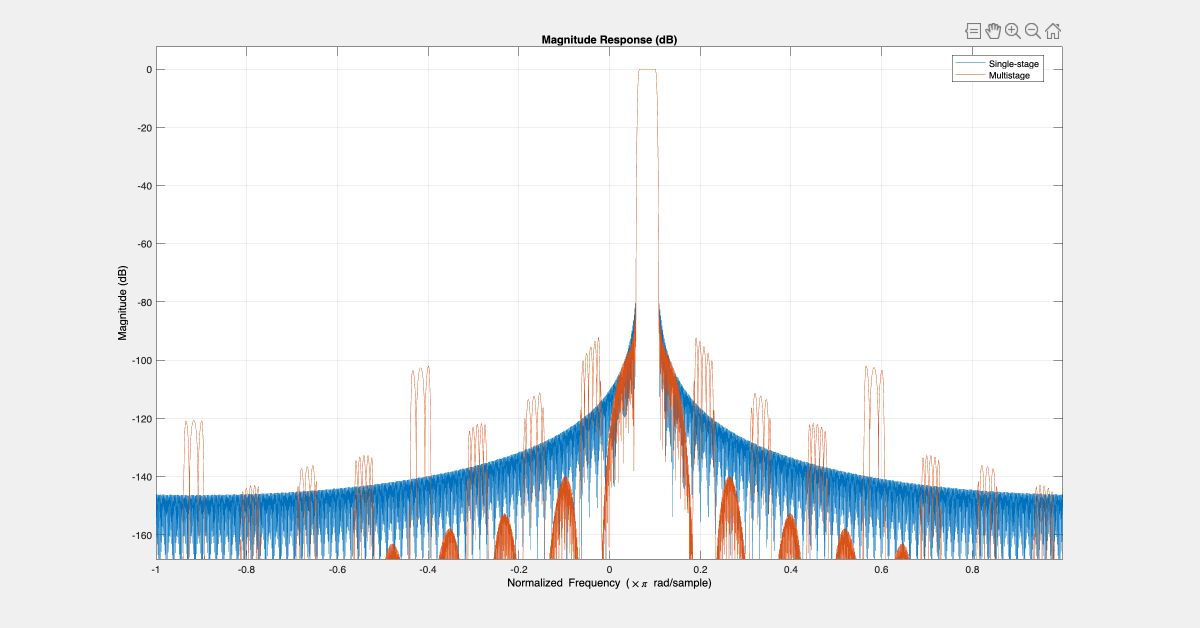
Finally, use the multistage filter to perform zoom FFT:

fftlen = 32;
L      = BWFactor * fftlen;
tones  = [1625 2000 2125]; % sine wave tones
sn     = dsp.SineWave(SampleRate=Fs, Frequency=tones, SamplesPerFrame=L);
Fsd    = Fs / BWFactor;
% Frequency points at which FFT is computed
F      = Fc + Fsd/fftlen*(0:fftlen-1)-Fsd/2;

% Step through the bandpass-decimator 
for k=1:100
    x = sum(sn(),2) +  1e-2 * randn(L,1);
    y = D_multi_stage(x);
end 

% Plot the spectral output
scopeZoomFFT = dsp.ArrayPlot(XDataMode="Custom",...
                   CustomXData=F,...
                   YLabel="Magnitude",...
                   XLabel="Frequency (Hz)",...
                   YLimits=[0 1],...
                   Title=sprintf ("Zoom FFT: Resolution = %f Hz",(Fs/BWFactor)/fftlen));

z = fft(y,fftlen,1);
z = fftshift(z);

scopeZoomFFT( abs(z)/fftlen )
release(scopeZoomFFT)

Using dsp.ZoomFFT

dsp.ZoomFFT is a System object that implements zoom FFT based on the multirate multistage bandpass filter described in the previous section. You specify the desired center frequency and decimation factor, and dsp.ZoomFFT will design the filter and apply it to the input signal.

Use dsp.ZoomFFT to zoom into the sine tones from the previous section's example:

zfft = dsp.ZoomFFT(BWFactor,Fc,Fs);
for k=1:100
    x = sum(sn(),2) + 1e-2 * randn(L,1);
    z = zfft(x);
end 

z = fftshift(z);
scopeZoomFFT( abs(z)/fftlen)

release(scopeZoomFFT)

References

[1] Multirate Signal Processing - Harris (Prentice Hall).

[2] Computing Translated Frequencies in digitizing and Downsampling Analog Bandpass - Lyons (https://www.dsprelated.com/showarticle/523.php)