Smoothing a Histogram

This example shows how to use spline commands from Curve Fitting Toolbox™ to smooth a histogram.

Here is a histogram of some random values that might represent data that were collected on some measurement.

y = randn(1,5001);
hist(y);

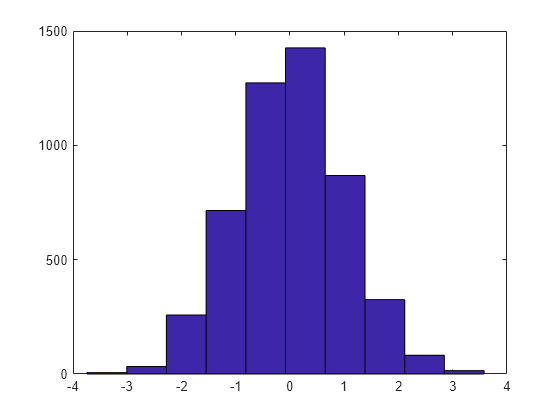
We would like to derive from this histogram a smoother approximation to the underlying distribution. We do this by constructing a spline function f whose average value over each bar interval equals the height of that bar.

If h is the height of one of these bars, and its left and right edges are at L and R, then we want the spline f to satisfy

integral {f(x) : L < x < R}/(R - L) = h,

or, with F the indefinite integral of f, i.e., DF = f,

F(R) - F(L) = h*(R - L).

[heights,centers] = hist(y);
hold on
ax = gca;
ax.XTickLabel = [];
n = length(centers);
w = centers(2)-centers(1);
t = linspace(centers(1)-w/2,centers(end)+w/2,n+1);
p = fix(n/2);
fill(t([p p p+1 p+1]),[0 heights([p p]),0],'w')
plot(centers([p p]),[0 heights(p)],'r:')
h = text(centers(p)-.2,heights(p)/2,'   h');
dep = -70;
tL = text(t(p),dep,'L');
tR = text(t(p+1),dep,'R');
hold off

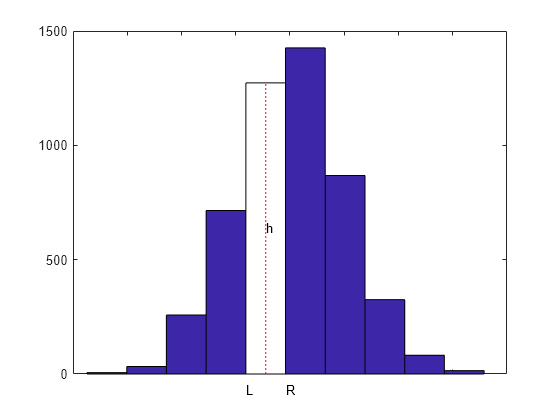
So, with n the number of bars, t(i) the left edge of the i-th bar, dt(i) its width, and h(i) its height, we want

F(t(i+1)) - F(t(i)) = h(i) * dt(i), for i = 1:n,

or, setting arbitrarily F(t(1)) = 0,

F(t(i)) = sum {h(j)*dt(j) : j=1:i-1}, for i = 1:n+1.

dt = diff(t);
Fvals = cumsum([0,heights.*dt]);

Add to this the two end conditions DF(t(1)) = 0 = DF(t(n+1)), and we have all the data we need to get F as a complete cubic spline interpolant.

F = spline(t, [0, Fvals, 0]);

The two extra zero values in the second argument indicate the zero endslope conditions.

Finally, the derivative, f = DF, of the spline F is the smoothed version of the histogram.

DF = fnder(F);  % computes its first derivative
h.String = 'h(i)';
tL.String = 't(i)';
tR.String = 't(i+1)';
hold on
fnplt(DF, 'r', 2)
hold off
ylims = ylim; 
ylim([0,ylims(2)]);