Evaluate Curve Fit
This example shows how to work with a curve fit.
Load Data and Fit a Polynomial Curve
load census curvefit = fit(cdate,pop,'poly3','normalize','on')
curvefit =
Linear model Poly3:
curvefit(x) = p1*x^3 + p2*x^2 + p3*x + p4
where x is normalized by mean 1890 and std 62.05
Coefficients (with 95% confidence bounds):
p1 = 0.921 (-0.9743, 2.816)
p2 = 25.18 (23.57, 26.79)
p3 = 73.86 (70.33, 77.39)
p4 = 61.74 (59.69, 63.8)
The output displays the fitted model equation, the fitted coefficients, and the confidence bounds for the fitted coefficients.
Plot the Fit, Data, Residuals, and Prediction Bounds
plot(curvefit,cdate,pop)

Plot the residuals fit.
plot(curvefit,cdate,pop,'Residuals')
Plot the prediction bounds on the fit.
plot(curvefit,cdate,pop,'predfunc')
Evaluate the Fit at a Specified Point
Evaluate the fit at a specific point by specifying a value for x , using this form: y = fittedmodel(x).
curvefit(1991)
ans = 252.6690
Evaluate the Fit Values at Many Points
Evaluate the model at a vector of values to extrapolate to the year 2050.
xi = (2000:10:2050).'; curvefit(xi)
ans = 6×1
276.9632
305.4420
335.5066
367.1802
400.4859
435.4468
Get prediction bounds on those values.
ci = predint(curvefit,xi)
ci = 6×2
267.8589 286.0674
294.3070 316.5770
321.5924 349.4208
349.7275 384.6329
378.7255 422.2462
408.5919 462.3017
Plot the fit and prediction intervals across the extrapolated fit range. By default, the fit is plotted over the range of the data. To see values extrapolated from the fit, set the upper x-limit of the axes to 2050 before plotting the fit. To plot prediction intervals, use predobs or predfun as the plot type.
plot(cdate,pop,'o') xlim([1900,2050]) hold on plot(curvefit,'predobs') hold off

Get the Model Equation
Enter the fit name to display the model equation, the fitted coefficients, and the confidence bounds for the fitted coefficients.
curvefit
curvefit =
Linear model Poly3:
curvefit(x) = p1*x^3 + p2*x^2 + p3*x + p4
where x is normalized by mean 1890 and std 62.05
Coefficients (with 95% confidence bounds):
p1 = 0.921 (-0.9743, 2.816)
p2 = 25.18 (23.57, 26.79)
p3 = 73.86 (70.33, 77.39)
p4 = 61.74 (59.69, 63.8)
To get only the model equation, use formula.
formula(curvefit)
ans = 'p1*x^3 + p2*x^2 + p3*x + p4'
Get Coefficient Names and Values
Specify a coefficient by name.
p1 = curvefit.p1
p1 = 0.9210
p2 = curvefit.p2
p2 = 25.1834
Get all the coefficient names. Look at the fit equation (for example, f(x) = p1*x^3+... ) to see the model terms for each coefficient.
coeffnames(curvefit)
ans = 4×1 cell
{'p1'}
{'p2'}
{'p3'}
{'p4'}
Get all the coefficient values.
coeffvalues(curvefit)
ans = 1×4
0.9210 25.1834 73.8598 61.7444
Get Confidence Bounds on the Coefficients
Use confidence bounds on coefficients to help you evaluate and compare fits. The confidence bounds on the coefficients determine their accuracy. Bounds that are far apart indicate uncertainty. If the bounds cross zero for linear coefficients, this means you cannot be sure that these coefficients differ from zero. If some model terms have coefficients of zero, then they are not helping with the fit.
confint(curvefit)
ans = 2×4
-0.9743 23.5736 70.3308 59.6907
2.8163 26.7931 77.3888 63.7981
Examine Goodness-of-Fit Statistics
To get goodness-of-fit statistics at the command line, you can either:
Open the Curve Fitter app. On the Curve Fitter tab, in the Export section, click Export and select Export to Workspace to export your fit and goodness of fit to the workspace.
Specify the
gofoutput argument using thefitfunction.
Recreate the fit specifying the gof and output arguments to get goodness-of-fit statistics and fitting algorithm information.
[curvefit,gof,output] = fit(cdate,pop,'poly3','normalize','on')
curvefit =
Linear model Poly3:
curvefit(x) = p1*x^3 + p2*x^2 + p3*x + p4
where x is normalized by mean 1890 and std 62.05
Coefficients (with 95% confidence bounds):
p1 = 0.921 (-0.9743, 2.816)
p2 = 25.18 (23.57, 26.79)
p3 = 73.86 (70.33, 77.39)
p4 = 61.74 (59.69, 63.8)
gof = struct with fields:
sse: 149.7687
rsquare: 0.9988
dfe: 17
adjrsquare: 0.9986
rmse: 2.9682
output = struct with fields:
numobs: 21
numparam: 4
residuals: [21×1 double]
Jacobian: [21×4 double]
exitflag: 1
algorithm: 'QR factorization and solve'
iterations: 1
Plot a histogram of the residuals to look for a roughly normal distribution.
histogram(output.residuals,10)

Plot the Fit, Data, and Residuals
plot(curvefit,cdate,pop,'fit','residuals') legend Location SouthWest
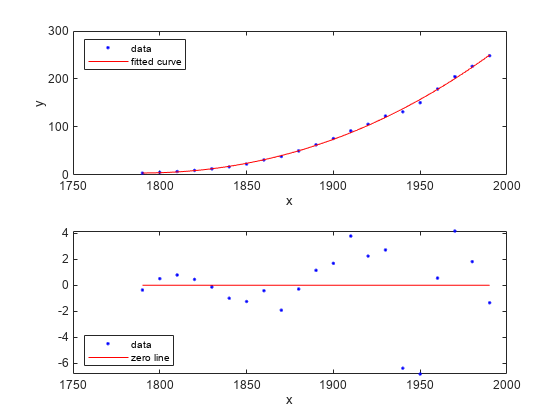
subplot(2,1,1) legend Location NorthWest
Find Methods
List every method that you can use with the fit.
methods(curvefit)
Methods for class cfit: argnames category cfit coeffnames coeffvalues confint dependnames differentiate feval fitoptions formula indepnames integrate islinear numargs numcoeffs plot predint probnames probvalues setoptions type
For more information on how to use a fit method, see cfit.