PM Demodulator Passband

Demodulate PM-modulated data

• 

Libraries:
Communications Toolbox / Modulation / Analog Passband Modulation

Description

The PM Demodulator Passband block demodulates a signal that was modulated using phase modulation. The input is a passband representation of the modulated signal. Both the input and output signals are real scalar signals.

Examples

Modulate and Demodulate PM Passband Signal in Simulink

Sample a 100 Hz linear frequency sweep chirp with a 400 Hz target frequency at 4 kilosamples per second. Modulate the input signal using the phas modulation method. Demodulate the signal. Plot the input signal, the modulated signal, and the demodulated signal.

The pmmoddemod_passband model modulates the input linear frequency sweep chirp signal using the PM method at a carrier frequency of 1.5 kHz with pi/2 phase deviation and then demodulates the signal. When the model runs, it plots the signals. This configuration ensures the Hilbert transform filter operates in the flat section of the magnitude response and that the demodulated signal has the desired magnitude and form.

The spectrum analyzer plot shows input signal, the modulated signal, and the demodulated signal.

Limitations

• This block does not work inside a triggered subsystem.

Ports

Input

In — Input signal

scalar

Input signal, specified as a scalar. The input is a passband representation of the modulated signal.

This port is unnamed on the block.

Data Types: double

Output

Out — Demodulated output signal

scalar

Demodulated output signal, returned as a scalar.

This port is unnamed on the block.

Data Types: double

Parameters

To edit block parameters interactively, use the Property Inspector. From the Simulink^® Toolstrip, on the Simulation tab, in the Prepare gallery, select Property Inspector.

Carrier frequency (Hz) — Carrier frequency in Hz

300 (default) | positive scalar

Carrier frequency in Hz, specified as a positive scalar.

Due to the implementation of the Hilbert transform by means of a filter, for best results, choose a carrier frequency, f_c, that exceeds the sample rate of the input signal by at least 10%.

Typically, an appropriate carrier frequency is a much higher than the highest frequency of the input signal. By the Nyquist sampling theorem, 1 / T_s > (2 × f_c), where T_s represents the sample time of the input signal. For more information, see Baseband vs. Passband Simulation.

Initial phase (rad) — Initial phase offset in radians

0 (default) | scalar

Initial phase offset of the carrier in radians, specified as a scalar.

Phase deviation (rad) — Phase deviation of carrier frequency in radians

pi/2 (default) | scalar

Phase deviation of the carrier frequency in radians, specified as a scalar. Also known as the variation in the phase.

Hilbert transform filter order (must be even) — Hilbert transform filter order

100 (default) | positive scalar

Hilbert transform filter order, specified as an even, positive scalar with a value greater than 2. This parameter value defines the length of the FIR filter used to compute the Hilbert transform.

Block Characteristics

Data Types	double
Multidimensional Signals	no
Variable-Size Signals	no

More About

Hilbert Transform Filter

To design the Hilbert transform filter, this block uses the Analytic Signal block, which computes the complex analytic signal corresponding to each channel of the real M-by-N input, u

$$y=u+j{\rm H}\left\{u\right\}$$

where $$j=\sqrt{-1}$$ and $${\rm H}\left\{\right\}$$ denotes the Hilbert transform. The real part of the output in each channel is a replica of the real input in that channel. The imaginary part is the Hilbert transform of the input. In the frequency domain, the analytic signal retains the positive frequency content of the original signal while zeroing-out negative frequencies and doubling the DC component.

The block computes the Hilbert transform using an equiripple FIR filter with the order that you specify using the Hilbert Transform filter order (must be even) parameter, n. This linear phase filter uses the Remez exchange algorithm and imposes a delay of n/2 on the input samples.

Because the block uses this filter, it requires a carrier frequency that exceeds the sample rate of the input signal by at least 10%.

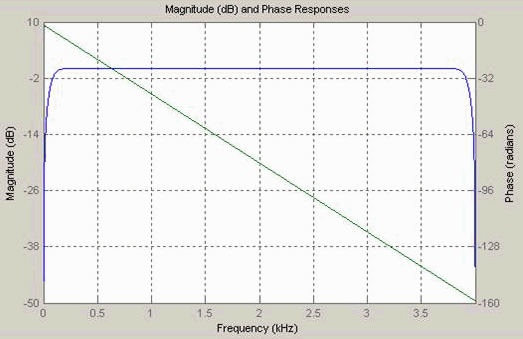
For example, this plot shows the response for a 10 Hz input signal at 8000 samples per second passed through a Hilbert transform filter of order 100.

A carrier frequency that is 10% to 90% higher than the sample rate of the input signal, ensures that the Hilbert transform filter operates in the flat section of its magnitude response (shown in blue) and that the modulated signal has the desired magnitude and form.

Extended Capabilities

C/C++ Code Generation
Generate C and C++ code using Simulink® Coder™.

Version History

Introduced before R2006a