Identifying Differentially Expressed Genes from RNA-Seq Data
This example shows how to test RNA-Seq data for differentially expressed genes using a negative binomial model.
Introduction
A typical differential expression analysis of RNA-Seq data consists of normalizing the raw counts and performing statistical tests to reject or accept the null hypothesis that two groups of samples show no significant difference in gene expression. This example shows how to inspect the basic statistics of raw count data, how to determine size factors for count normalization and how to infer the most differentially expressed genes using a negative binomial model.
The dataset for this example comprises of RNA-Seq data obtained in the experiment described by Brooks et al. [1]. The authors investigated the effect of siRNA knock-down of pasilla, a gene known to play an important role in the regulation of splicing in Drosophila melanogaster. The dataset consists of 2 biological replicates of the control (untreated) samples and 2 biological replicates of the knock-down (treated) samples.
Inspecting Read Count Tables for Genomic Features
The starting point for this analysis of RNA-Seq data is a count matrix, where the rows correspond to genomic features of interest, the columns correspond to the given samples and the values represent the number of reads mapped to each feature in a given sample.
The included file pasilla_count_noMM.mat contains two tables with the count matrices at the gene level and at the exon level for each of the considered samples. You can obtain similar matrices using the function featurecount.
load pasilla_count_noMM.mat
% preview the table of read counts for genes
head(geneCountTable)
ID Reference untreated3 untreated4 treated2 treated3
_____________ _________ __________ __________ ________ ________
"FBgn0000003" "3R" 0 1 1 2
"FBgn0000008" "2R" 142 117 138 132
"FBgn0000014" "3R" 20 12 10 19
"FBgn0000015" "3R" 2 4 0 1
"FBgn0000017" "3L" 6591 5127 4809 6027
"FBgn0000018" "2L" 469 530 492 574
"FBgn0000024" "3R" 5 6 10 8
"FBgn0000028" "X" 0 0 2 1
Note that when counting is performed without summarization, the individual features (exons in this case) are reported with their metafeature assignment (genes in this case) followed by the start and stop positions.
% preview the table of read counts for exons
head(exonCountTable)
ID Reference untreated3 untreated4 treated2 treated3
_______________________________ _________ __________ __________ ________ ________
"FBgn0000003_2648220_2648518" "3R" 0 0 0 1
"FBgn0000008_18024938_18025756" "2R" 0 1 0 2
"FBgn0000008_18050410_18051199" "2R" 13 9 14 12
"FBgn0000008_18052282_18052494" "2R" 4 2 5 0
"FBgn0000008_18056749_18058222" "2R" 32 27 26 23
"FBgn0000008_18058283_18059490" "2R" 14 18 29 22
"FBgn0000008_18059587_18059757" "2R" 1 4 3 0
"FBgn0000008_18059821_18059938" "2R" 0 0 2 0
You can annotate and group the samples by creating a logical vector as follows:
samples = geneCountTable(:,3:end).Properties.VariableNames; untreated = strncmp(samples,'untreated',length('untreated')) treated = strncmp(samples,'treated',length('treated'))
untreated = 1×4 logical array 1 1 0 0 treated = 1×4 logical array 0 0 1 1
Plotting the Feature Assignments
The included file also contains a table geneSummaryTable with the summary of assigned and unassigned SAM entries. You can plot the basic distribution of the counting results by considering the number of reads that are assigned to the given genomic features (exons or genes for this example), as well as the number of reads that are unassigned (i.e. not overlapping any feature) or ambiguous (i.e. overlapping multiple features).
st = geneSummaryTable({'Assigned','Unassigned_ambiguous','Unassigned_noFeature'},:)
bar(table2array(st)','stacked');
legend(st.Properties.RowNames','Interpreter','none','Location','southeast');
xlabel('Sample')
ylabel('Number of reads')
st =
3×4 table
untreated3 untreated4 treated2 treated3
__________ __________ __________ __________
Assigned 1.5457e+07 1.6302e+07 1.5146e+07 1.8856e+07
Unassigned_ambiguous 1.5708e+05 1.6882e+05 1.6194e+05 1.9977e+05
Unassigned_noFeature 7.5455e+05 5.8309e+05 5.8756e+05 6.8356e+05
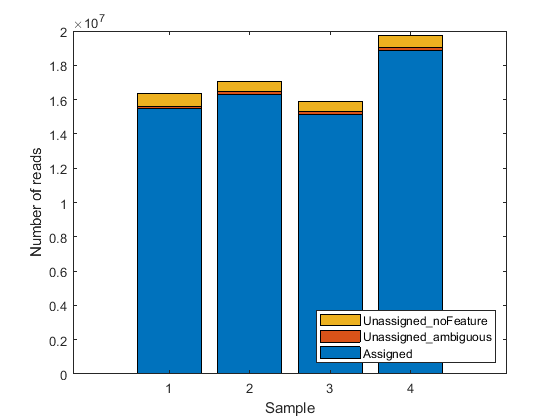
Note that a small fraction of the alignment records in the SAM files is not reported in the summary table. You can notice this in the difference between the total number of records in a SAM file and the total number of records processed during the counting procedure for that same SAM file. These unreported records correspond to the records mapped to reference sequences that are not annotated in the GTF file and therefore are not processed in the counting procedure. If the gene models account for all the reference sequences used during the read mapping step, then all records are reported in one of the categories of the summary table.
geneSummaryTable{'TotalEntries',:} - sum(geneSummaryTable{2:end,:})
ans =
89516 95885 98207 104629
Plotting Read Coverage Across a Given Chromosome
When read counting is performed without summarization using the function featurecount, the default IDs are composed by the attribute or metafeature (by default, gene_id) followed by the start and the stop positions of the feature (by default, exon). You can use the exon start positions to plot the read coverage across any chromosome in consideration, for example chromosome arm 2L.
% consider chromosome arm 2L chr2L = strcmp(exonCountTable.Reference,'2L'); exonCount = exonCountTable{:,3:end}; % retrieve exon start positions exonStart = regexp(exonCountTable{chr2L,1},'_(\d+)_','tokens'); exonStart = [exonStart{:}]; exonStart = cellfun(@str2num, [exonStart{:}]'); % sort exon by start positions [~,idx] = sort(exonStart); % plot read coverage along the genomic coordinates figure; plot(exonStart(idx),exonCount(idx,treated),'.-r',... exonStart(idx),exonCount(idx,untreated),'.-b'); xlabel('Genomic position'); ylabel('Read count (exon level)'); title('Read count on Chromosome arm 2L'); % plot read coverage for each group separately figure; subplot(2,1,1); plot(exonStart(idx),exonCount(idx,untreated),'.-r'); ylabel('Read count (exon level)'); title('Chromosome arm 2L (treated samples)'); subplot(2,1,2); plot(exonStart(idx),exonCount(idx,treated),'.-b'); ylabel('Read count (exon level)'); xlabel('Genomic position'); title('Chromosome arm 2L (untreated samples)');
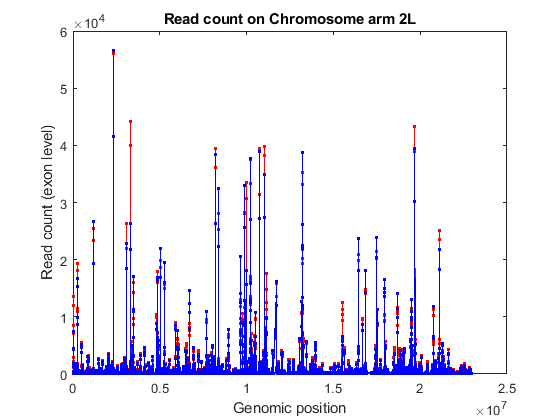
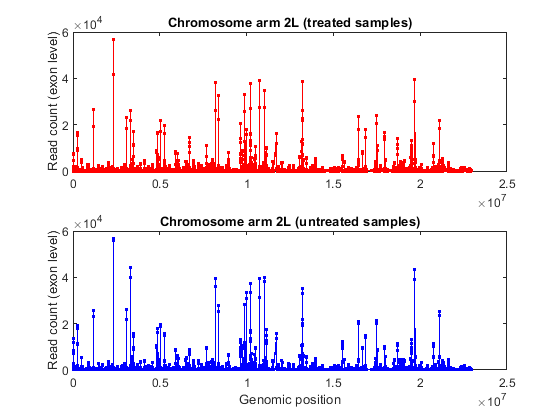
Alternatively, you can plot the read coverage considering the starting position of each gene in a given chromosome. The file pasilla_geneLength.mat contains a table with the start and stop position of each gene in the corresponding gene annotation file.
% load gene start and stop position information load pasilla_geneLength head(geneLength)
ID Name Reference Start Stop
_____________ _________ _________ _____ _____
"FBgn0037213" "CG12581" 3R 380 10200
"FBgn0000500" "Dsk" 3R 15388 16170
"FBgn0053294" "CR33294" 3R 17136 21871
"FBgn0037215" "CG12582" 3R 23029 30295
"FBgn0037217" "CG14636" 3R 30207 41033
"FBgn0037218" "aux" 3R 37505 53244
"FBgn0051516" "CG31516" 3R 44179 45852
"FBgn0261436" "DhpD" 3R 53106 54971
% consider chromosome 3 ('Reference' is a categorical variable) chr3 = (geneLength.Reference == '3L') | (geneLength.Reference == '3R'); sum(chr3) % consider the counts for genes in chromosome 3 counts = geneCountTable{:,3:end}; [~,j,k] = intersect(geneCountTable{:,'ID'},geneLength{chr3,'ID'}); gstart = geneLength{k,'Start'}; gcounts = counts(j,:); % sort according to ascending start position [~,idx] = sort(gstart); % plot read coverage by genomic position figure; plot(gstart(idx), gcounts(idx,treated),'.-r',... gstart(idx), gcounts(idx,untreated),'.-b'); xlabel('Genomic position') ylabel('Read count'); title('Read count on Chromosome 3');
ans =
6360
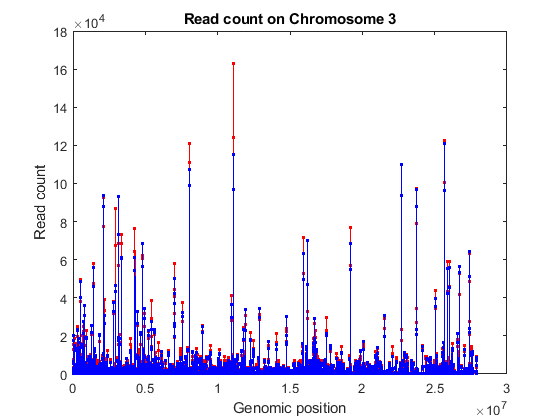
Normalizing Read Counts
The read count in RNA-Seq data has been found to be linearly related to the abundance of transcripts [2]. However, the read count for a given gene depends not only on the expression level of the gene, but also on the total number of reads sequenced and the length of the gene transcript. Therefore, in order to infer the expression level of a gene from the read count, we need to account for the sequencing depth and the gene transcript length. One common technique to normalize the read count is to use the RPKM (Read Per Kilobase Mapped) values, where the read count is normalized by the total number of reads yielded (in millions) and the length of each transcript (in kilobases). This normalization technique, however, is not always effective since few, very highly expressed genes can dominate the total lane count and skew the expression analysis.
A better normalization technique consists of computing the effective library size by considering a size factor for each sample. By dividing each sample's counts by the corresponding size factors, we bring all the count values to a common scale, making them comparable. Intuitively, if sample A is sequenced N times deeper than sample B, the read counts of non-differentially expressed genes are expected to be on average N times higher in sample A than in sample B, even if there is no difference in expression.
To estimate the size factors, take the median of the ratios of observed counts to those of a pseudo-reference sample, whose counts can be obtained by considering the geometric mean of each gene across all samples [3]. Then, to transform the observed counts to a common scale, divide the observed counts in each sample by the corresponding size factor.
% estimate pseudo-reference with geometric mean row by row
pseudoRefSample = geomean(counts,2);
nz = pseudoRefSample > 0;
ratios = bsxfun(@rdivide,counts(nz,:),pseudoRefSample(nz));
sizeFactors = median(ratios,1)
sizeFactors =
0.9374 0.9725 0.9388 1.1789
% transform to common scale
normCounts = bsxfun(@rdivide,counts,sizeFactors);
normCounts(1:10,:)
ans =
1.0e+03 *
0 0.0010 0.0011 0.0017
0.1515 0.1203 0.1470 0.1120
0.0213 0.0123 0.0107 0.0161
0.0021 0.0041 0 0.0008
7.0315 5.2721 5.1225 5.1124
0.5003 0.5450 0.5241 0.4869
0.0053 0.0062 0.0107 0.0068
0 0 0.0021 0.0008
1.2375 1.1753 1.2122 1.2003
0 0 0 0.0008
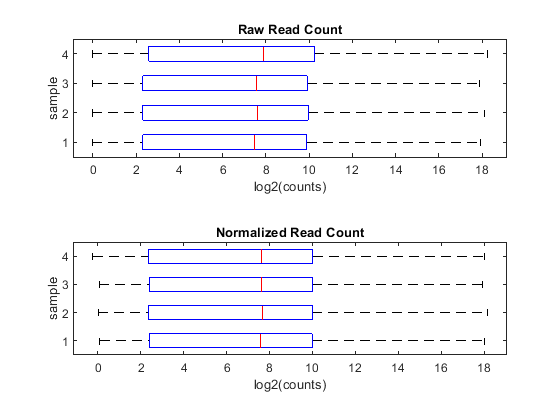
You can appreciate the effect of this normalization by using the function boxplot to represent statistical measures such as median, quartiles, minimum and maximum.
figure; subplot(2,1,1) maboxplot(log2(counts),'title','Raw Read Count','orientation','horizontal') ylabel('sample') xlabel('log2(counts)') subplot(2,1,2) maboxplot(log2(normCounts),'title','Normalized Read Count','orientation','horizontal') ylabel('sample') xlabel('log2(counts)')
Computing Mean, Dispersion and Fold Change
In order to better characterize the data, we consider the mean and the dispersion of the normalized counts. The variance of read counts is given by the sum of two terms: the variation across samples (raw variance) and the uncertainty of measuring the expression by counting reads (shot noise or Poisson). The raw variance term dominates for highly expressed genes, whereas the shot noise dominates for lowly expressed genes. You can plot the empirical dispersion values against the mean of the normalized counts in a log scale as shown below.
% consider the mean meanTreated = mean(normCounts(:,treated),2); meanUntreated = mean(normCounts(:,untreated),2); % consider the dispersion dispTreated = std(normCounts(:,treated),0,2) ./ meanTreated; dispUntreated = std(normCounts(:,untreated),0,2) ./ meanUntreated; % plot on a log-log scale figure; loglog(meanTreated,dispTreated,'r.'); hold on; loglog(meanUntreated,dispUntreated,'b.'); xlabel('log2(Mean)'); ylabel('log2(Dispersion)'); legend('Treated','Untreated','Location','southwest');
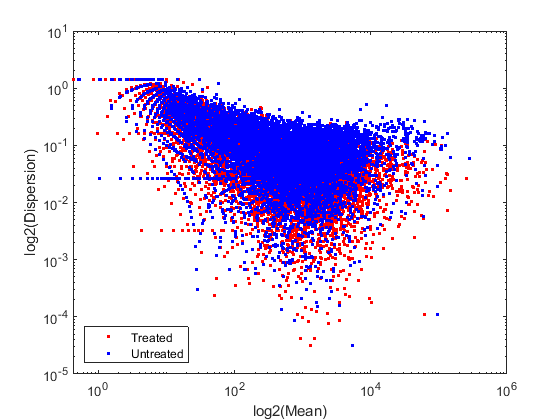
Given the small number of replicates, it is not surprising to expect that the dispersion values scatter with some variance around the true value. Some of this variance reflects sampling variance and some reflects the true variability among the gene expressions of the samples.
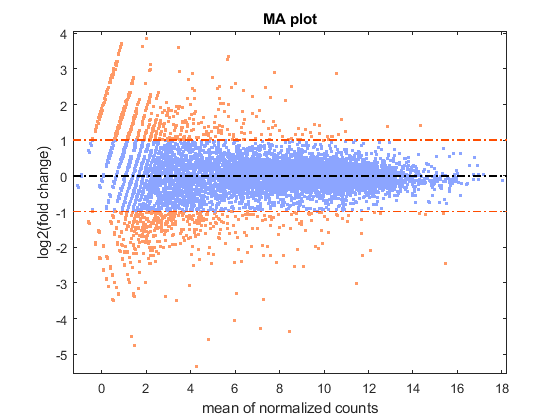
You can look at the difference of the gene expression among two conditions, by calculating the fold change (FC) for each gene, i.e. the ratio between the counts in the treated group over the counts in the untreated group. Generally these ratios are considered in the log2 scale, so that any change is symmetric with respect to zero (e.g. a ratio of 1/2 or 2/1 corresponds to -1 or +1 in the log scale).
% compute the mean and the log2FC meanBase = (meanTreated + meanUntreated) / 2; foldChange = meanTreated ./ meanUntreated; log2FC = log2(foldChange); % plot mean vs. fold change (MA plot) mairplot(meanTreated, meanUntreated,'Type','MA','Plotonly',true); set(get(gca,'Xlabel'),'String','mean of normalized counts') set(get(gca,'Ylabel'),'String','log2(fold change)')
Warning: Zero values are ignored
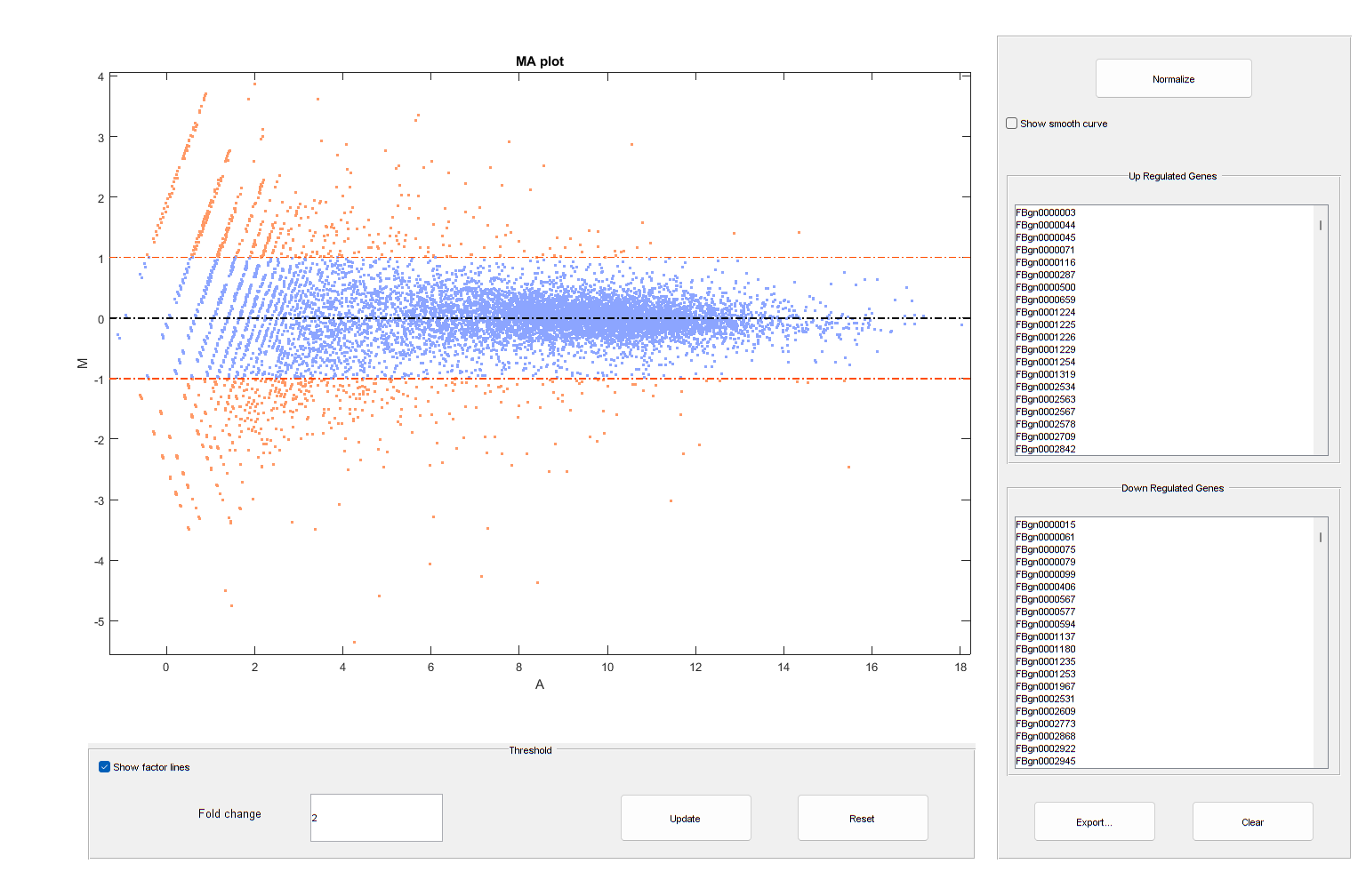
It is possible to annotate the values in the plot with the corresponding gene names, interactively select genes, and export gene lists to the workspace by calling the mairplot function as illustrated below:
mairplot(meanTreated,meanUntreated,'Labels',geneCountTable.ID,'Type','MA');
Warning: Zero values are ignored
It is convenient to store the information about the mean value and fold change for each gene in a table. You can then access information about a given gene or a group of genes satisfying specific criteria by indexing the table by gene names.
% create table with statistics about each gene
geneTable = table(meanBase,meanTreated,meanUntreated,foldChange,log2FC);
geneTable.Properties.RowNames = geneCountTable.ID;
% summary
summary(geneTable)
Variables:
meanBase: 11609×1 double
Values:
Min 0.21206
Median 201.24
Max 2.6789e+05
meanTreated: 11609×1 double
Values:
Min 0
Median 201.54
Max 2.5676e+05
meanUntreated: 11609×1 double
Values:
Min 0
Median 199.44
Max 2.7903e+05
foldChange: 11609×1 double
Values:
Min 0
Median 0.99903
Max Inf
log2FC: 11609×1 double
Values:
Min -Inf
Median -0.001406
Max Inf
% preview
head(geneTable)
meanBase meanTreated meanUntreated foldChange log2FC
________ ___________ _____________ __________ _________
FBgn0000003 0.9475 1.3808 0.51415 2.6857 1.4253
FBgn0000008 132.69 129.48 135.9 0.95277 -0.069799
FBgn0000014 15.111 13.384 16.838 0.79488 -0.33119
FBgn0000015 1.7738 0.42413 3.1234 0.13579 -2.8806
FBgn0000017 5634.6 5117.4 6151.8 0.83186 -0.26559
FBgn0000018 514.08 505.48 522.67 0.96711 -0.048243
FBgn0000024 7.2354 8.7189 5.752 1.5158 0.60009
FBgn0000028 0.74465 1.4893 0 Inf Inf
% access information about a specific gene myGene = 'FBgn0261570'; geneTable(myGene,:) geneTable(myGene,{'meanBase','log2FC'}) % access information about a given gene list myGeneSet = ["FBgn0261570","FBgn0261573","FBgn0261575","FBgn0261560"]; geneTable(myGeneSet,:)
ans =
1×5 table
meanBase meanTreated meanUntreated foldChange log2FC
________ ___________ _____________ __________ _______
FBgn0261570 4435.5 4939.1 3931.8 1.2562 0.32907
ans =
1×2 table
meanBase log2FC
________ _______
FBgn0261570 4435.5 0.32907
ans =
4×5 table
meanBase meanTreated meanUntreated foldChange log2FC
________ ___________ _____________ __________ _______
FBgn0261570 4435.5 4939.1 3931.8 1.2562 0.32907
FBgn0261573 2936.9 2954.8 2919.1 1.0122 0.01753
FBgn0261575 4.3776 5.6318 3.1234 1.8031 0.85047
FBgn0261560 2041.1 1494.3 2588 0.57738 -0.7924
Inferring Differential Expression with a Negative Binomial Model
Determining whether the gene expressions in two conditions are statistically different consists of rejecting the null hypothesis that the two data samples come from distributions with equal means. This analysis assumes the read counts are modeled according to a negative binomial distribution (as proposed in [3]). The function rnaseqde performs this type of hypothesis testing with three possible options to specify the type of linkage between the variance and the mean.
By specifying the link between variance and mean as an identity, we assume the variance is equal to the mean, and the counts are modeled by the Poisson distribution [4]. "IDColumns" specifies columns from the input table to append to the output table to help keep data organized.
diffTableIdentity = rnaseqde(geneCountTable,["untreated3","untreated4"],["treated2","treated3"],VarianceLink="identity",IDColumns="ID"); % Preview the results. head(diffTableIdentity)
ID Mean1 Mean2 Log2FoldChange PValue AdjustedPValue
_____________ _______ _______ ______________ _________ ______________
"FBgn0000003" 0.51415 1.3808 1.4253 0.627 0.75892
"FBgn0000008" 135.9 129.48 -0.069799 0.48628 0.64516
"FBgn0000014" 16.838 13.384 -0.33119 0.44445 0.61806
"FBgn0000015" 3.1234 0.42413 -2.8806 0.05835 0.12584
"FBgn0000017" 6151.8 5117.4 -0.26559 2.864e-42 6.0233e-41
"FBgn0000018" 522.67 505.48 -0.048243 0.39015 0.5616
"FBgn0000024" 5.752 8.7189 0.60009 0.35511 0.52203
"FBgn0000028" 0 1.4893 Inf 0.252 0.39867
Alternatively, by specifying the variance as the sum of the shot noise term (i.e. mean) and a constant multiplied by the squared mean, the counts are modeled according to a distribution described in [5]. The constant term is estimated using all the rows in the data.
diffTableConstant = rnaseqde(geneCountTable,["untreated3","untreated4"],["treated2","treated3"],VarianceLink="constant",IDColumns="ID"); % Preview the results. head(diffTableConstant)
ID Mean1 Mean2 Log2FoldChange PValue AdjustedPValue
_____________ _______ _______ ______________ __________ ______________
"FBgn0000003" 0.51415 1.3808 1.4253 0.62769 0.7944
"FBgn0000008" 135.9 129.48 -0.069799 0.53367 0.72053
"FBgn0000014" 16.838 13.384 -0.33119 0.45592 0.68454
"FBgn0000015" 3.1234 0.42413 -2.8806 0.058924 0.16938
"FBgn0000017" 6151.8 5117.4 -0.26559 8.5529e-05 0.00077269
"FBgn0000018" 522.67 505.48 -0.048243 0.54834 0.73346
"FBgn0000024" 5.752 8.7189 0.60009 0.36131 0.58937
"FBgn0000028" 0 1.4893 Inf 0.2527 0.46047
Finally, by considering the variance as the sum of the shot noise term (i.e. mean) and a locally regressed non-parametric smooth function of the mean, the counts are modeled according to the distribution proposed in [3].
diffTableLocal = rnaseqde(geneCountTable,["untreated3","untreated4"],["treated2", "treated3"],VarianceLink="local",IDColumns="ID"); % Preview the results. head(diffTableLocal)
ID Mean1 Mean2 Log2FoldChange PValue AdjustedPValue
_____________ _______ _______ ______________ _________ ______________
"FBgn0000003" 0.51415 1.3808 1.4253 1 1
"FBgn0000008" 135.9 129.48 -0.069799 0.67298 0.89231
"FBgn0000014" 16.838 13.384 -0.33119 0.6421 0.87234
"FBgn0000015" 3.1234 0.42413 -2.8806 0.22776 0.57215
"FBgn0000017" 6151.8 5117.4 -0.26559 0.0014429 0.014207
"FBgn0000018" 522.67 505.48 -0.048243 0.65307 0.88136
"FBgn0000024" 5.752 8.7189 0.60009 0.55154 0.81984
"FBgn0000028" 0 1.4893 Inf 0.42929 0.7765
The output of rnaseqde includes a vector of P-values. A P-value indicates the probability that a change in expression as strong as the one observed (or even stronger) would occur under the null hypothesis, i.e. the conditions have no effect on gene expression. In the histogram of the P-values we observe an enrichment of low values (due to differentially expressed genes), whereas other values are uniformly spread (due to non-differentially expressed genes). The enrichment of values equal to 1 are due to genes with very low counts.
figure; histogram(diffTableLocal.PValue,100) xlabel('P-value') ylabel('Frequency') title('P-value enrichment')
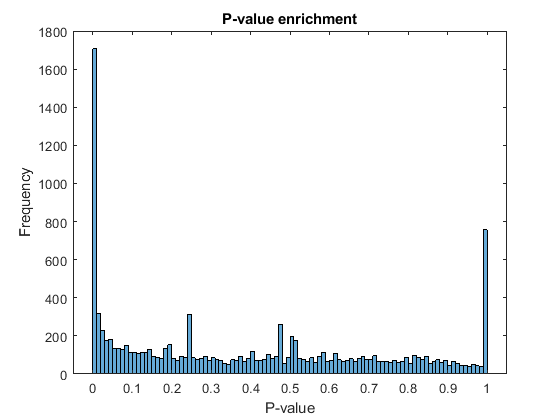
Filter out those genes with relatively low count to observe a more uniform spread of non-significant P-values across the range (0,1]. Note that this does not affect the distribution of significant P-values.
lowCountThreshold = 10; lowCountGenes = all(counts < lowCountThreshold, 2); histogram(diffTableLocal.PValue(~lowCountGenes),100) xlabel('P-value') ylabel('Frequency') title('P-value enrichment without low count genes')
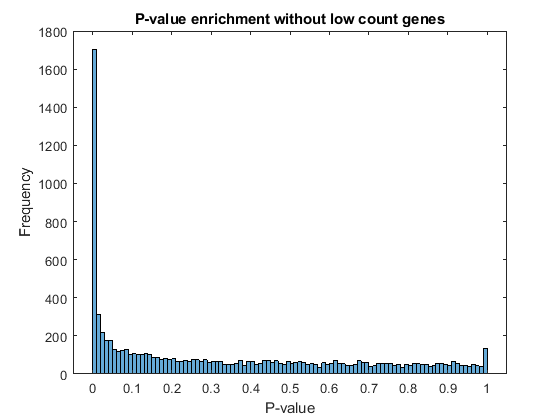
Multiple Testing and Adjusted P-values
Thresholding P-values to determine what fold changes are more significant than others is not appropriate for this type of data analysis, due to the multiple testing problem. While performing a large number of simultaneous tests, the probability of getting a significant result simply due to chance increases with the number of tests. In order to account for multiple testing, perform a correction (or adjustment) of the P-values so that the probability of observing at least one significant result due to chance remains below the desired significance level.
The Benjamini-Hochberg adjustment [6] is a statistical method that provides an adjusted P-value answering the following question: what would be the fraction of false positives if all the genes with adjusted P-values below a given threshold were considered significant?
The output of rnaseqde includes a vector of adjusted P-values in the "AdjustedPValue" field. By default, the P-values are adjusted using the Benjamini-Hochberg adjustment. Alternatively, the "FDRMethod" Name-Value argument in rnaseqde can be set to "storey" to perform Storey's procedure [7].
Set a threshold of 0.1 for the adjusted P-values, equivalent to consider a 10% false positives as acceptable, and identify the genes that are significantly expressed by considering all the genes with adjusted P-values below this threshold.
% create a table with significant genes sig = diffTableLocal.AdjustedPValue < 0.1; diffTableLocalSig = diffTableLocal(sig,:); diffTableLocalSig = sortrows(diffTableLocalSig,'AdjustedPValue'); numberSigGenes = size(diffTableLocalSig,1)
numberSigGenes =
1904
Identifying the Most Up-regulated and Down-regulated Genes
You can now identify the most up-regulated or down-regulated genes by considering an absolute fold change above a chosen cutoff. For example, a cutoff of 1 in log2 scale yields the list of genes that are up-regulated with a 2 fold change.
% find up-regulated genes up = diffTableLocalSig.Log2FoldChange > 1; upGenes = sortrows(diffTableLocalSig(up,:),'Log2FoldChange','descend'); numberSigGenesUp = sum(up) % display the top 10 up-regulated genes top10GenesUp = upGenes(1:10,:) % find down-regulated genes down = diffTableLocalSig.Log2FoldChange < -1; downGenes = sortrows(diffTableLocalSig(down,:),'Log2FoldChange','ascend'); numberSigGenesDown = sum(down) % find top 10 down-regulated genes top10GenesDown = downGenes(1:10,:)
numberSigGenesUp =
129
top10GenesUp =
10×6 table
ID Mean1 Mean2 Log2FoldChange PValue AdjustedPValue
_____________ ______ ______ ______________ __________ ______________
"FBgn0030173" 0 6.7957 Inf 0.0063115 0.047764
"FBgn0036822" 0 6.2729 Inf 0.012203 0.079274
"FBgn0052548" 1.0476 15.269 3.8654 0.00016945 0.0022662
"FBgn0050495" 1.0283 12.635 3.6191 0.0018949 0.017972
"FBgn0063667" 3.1042 38.042 3.6153 8.5037e-08 2.3845e-06
"FBgn0033764" 16.324 167.61 3.3601 1.8345e-25 2.9174e-23
"FBgn0037290" 16.228 155.46 3.26 3.5583e-23 4.6941e-21
"FBgn0033733" 1.5424 13.384 3.1172 0.0027276 0.024283
"FBgn0037191" 1.6003 12.753 2.9945 0.0047803 0.038193
"FBgn0033943" 1.581 12.319 2.962 0.0053635 0.041986
numberSigGenesDown =
181
top10GenesDown =
10×6 table
ID Mean1 Mean2 Log2FoldChange PValue AdjustedPValue
_____________ ______ _______ ______________ __________ ______________
"FBgn0053498" 30.938 0 -Inf 9.8404e-11 4.345e-09
"FBgn0259236" 13.618 0 -Inf 1.5526e-05 0.00027393
"FBgn0052500" 8.7405 0 -Inf 0.00066783 0.0075343
"FBgn0039331" 7.3908 0 -Inf 0.0019558 0.018474
"FBgn0040697" 6.8381 0 -Inf 0.0027378 0.024336
"FBgn0034972" 5.8291 0 -Inf 0.0068564 0.05073
"FBgn0040967" 5.2764 0 -Inf 0.0096039 0.065972
"FBgn0031923" 4.7429 0 -Inf 0.016164 0.098762
"FBgn0085359" 121.97 2.9786 -5.3557 5.5813e-33 1.5068e-30
"FBgn0004854" 14.402 0.53259 -4.7571 8.1587e-05 0.0012034
A good visualization of the gene expressions and their significance is given by plotting the fold change versus the mean in log scale and coloring the data points according to the adjusted P-values.
figure scatter(log2(geneTable.meanBase),diffTableLocal.Log2FoldChange,3,diffTableLocal.PValue,'o') colormap(flipud(cool(256))) colorbar; ylabel('log2(Fold Change)') xlabel('log2(Mean of normalized counts)') title('Fold change by FDR')
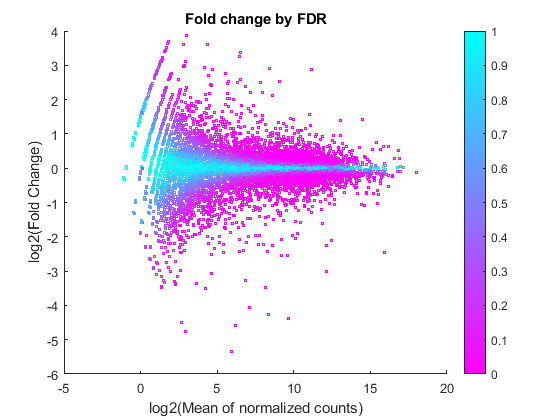
You can see here that for weakly expressed genes (i.e. those with low means), the FDR is generally high because low read counts are dominated by Poisson noise and consequently any biological variability is drowned in the uncertainties from the read counting.
References
[1] Brooks et al. Conservation of an RNA regulatory map between Drosophila and mammals. Genome Research 2011. 21:193-202.
[2] Mortazavi et al. Mapping and quantifying mammalian transcriptomes by RNA-Seq. Nature Methods 2008. 5:621-628.
[3] Anders et al. Differential expression analysis for sequence count data. Genome Biology 2010. 11:R106.
[4] Marioni et al. RNA-Seq: An assessment of technical reproducibility and comparison with gene expression arrays. Genome Research 2008. 18:1509-1517.
[5] Robinson et al. Moderated statistical test for assessing differences in tag abundance. Bioinformatics 2007. 23(21):2881-2887.
[6] Benjamini et al. Controlling the false discovery rate: a practical and powerful approach to multiple testing. 1995. Journal of the Royal Statistical Society, Series B57 (1):289-300.
[7] J.D. Storey. "A direct approach to false discovery rates", Journal of the Royal Statistical Society, B (2002), 64(3), pp.479-498.
See Also
featurecount | nbintest | mairplot | plotVarianceLink