CI Engine Speed-Density Air Mass Flow Model
To calculate the air mass flow in the compression-ignition (CI) engine, the CI Core Engine block uses a speed-density air mass flow model. The speed-density model uses the speed-density equation to calculate the engine air mass flow. The equation relates the engine air mass flow to the intake manifold gas pressure, intake manifold gas temperature, and engine speed. In the CI Core Engine block, the air mass flow and the cylinder air mass determine the engine load.
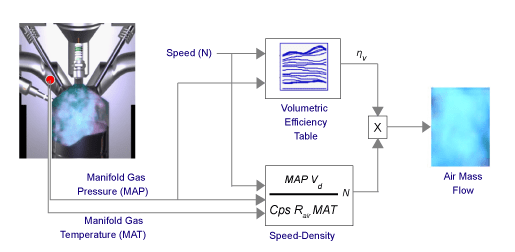
To determine the air mass flow, the speed-density air mass flow model uses this speed-density equation at the intake manifold and the volumetric efficiency. The model subtracts the exhaust gas recirculation (EGR) burned gas from the mass flow at the intake port.
The speed-density air mass flow model uses a volumetric efficiency lookup table to determine the volumetric efficiency.
The volumetric efficiency lookup table is a function of the intake manifold absolute pressure at intake valve closing (IVC) and engine speed
where:
is engine volumetric efficiency, dimensionless.
MAP is intake manifold absolute pressure, in KPa.
N is engine speed, in rpm.

To create the volumetric efficiency table, use the air mass flow rate from measured engine performance data and the speed-density equation.
To calculate the engine load, the block divides the calculated unburned air mass by the nominal cylinder air mass. The nominal cylinder air mass is the mass of air (in kg) in a cylinder with the piston at bottom dead center (BDC), at standard air temperature and pressure.
The model implements equations that use these variables.
Engine air mass flow | |
Cycle average intake manifold pressure | |
Total engine air mass flow at intake ports, including EGR flow | |
Recirculated burned gas mass flow entering engine intake port | |
Displaced volume | |
| N | Engine speed |
Crankshaft revolutions per power stroke | |
Ideal gas constant for air and burned gas mixture | |
Cycle average intake manifold gas absolute temperature | |
Engine volumetric efficiency | |
Engine volumetric efficiency lookup table | |
| L | Engine load (normalized cylinder air mass) at arbitrary cam phaser angles, corrected for final steady-state cam phaser angles |
Nominal engine cylinder air mass at standard temperature and pressure; piston at bottom dead center (BDC) maximum volume | |
| Standard pressure | |
| Standard temperature |
References
[1] Heywood, John B. Internal Combustion Engine Fundamentals. New York: McGraw-Hill, 1988.
See Also
CI Core Engine | CI Controller